Глубинный остовный лес

В процессе обхода ориентированного графа методом поиска в глубину только определенные дуги ведут к вершинам, которые ранее не посещались. Такие дуги, ведущие к новым вершинам, называются дугами дерева и формируют для данного графа глубинный остовный лес, построенный методом поиска в глубину. На рис. 49 показан глубинный остовный лес для графа из рис. 48. На рисунке леса сплошными линиями обозначены дуги дерева. Именно они формируют лес, поскольку методом поиска в глубину к любой ранее не посещавшейся вершине можно придти только по одной дуге.

Рис. 49 – Глубинный остовный лес

Кроме дуг дерева, существуют еще три типа дуг, определяемых в процессе обхода орграфа методом поиска в глубину. Это обратные, прямые и поперечные дуги. Обратные дуги, как дуга C→A. Они в остовном лесу идут от потомков к предкам. Дуга из вершины в саму себя также является обратной дугой. Прямыми дугами называются дуги, идущие от предков к истинным потомкам, но которые не являются дугами дерева. На рис. 49 прямые дуги отсутствуют.

Дуги, таки как D→C и G→D, соединяющие вершины, не являющиеся ни предками, ни потомками друг друга, называются поперечными дугами. Если при построении остовного дерева сыновья одной вершины располагаются слева направо, то все поперечные дуги идут справа налево. Такое расположение вершин и деревьев помогает формировать остовный лес.

Дуги дерева легко отличить от других, т.к. они получаются в процессе обхода графа как дуги, ведущие к тем вершинам, которые ранее не посещались. Если v – вершина орграфа, то всем потомкам вершины v присваиваются глубинные номера, не меньшие, чем номер, присвоенный вершине v. Фактически вершина w будет потомком вершины v тогда и только тогда, когда выполняются неравенства:

dfnumber(v) dfnumber(w) 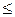dfnumber (v)+количество потомков вершины v.

Очевидно, что прямые дуги идут от вершин с низкими номерами к вершинам с более высокими номерами, а обратные и поперечные дуги – от вершин с высокими номерами к вершинам с более низкими номерами.

Лекция 15

План лекции:

1. Модель внешних вычислений.

2. Особенности операций с внешней памятью.

3. Организация данных в файлах.

4. Хешированные файлы.

5. Индексированные файлы.

6. Несортированные файлы с плотным индексом.

Не нашли, что искали? Воспользуйтесь поиском: