VII. Односторонние пределы.

I. Пределы числовых последовательностей.

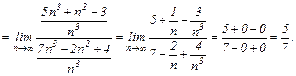
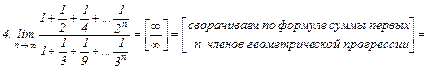
5.

.

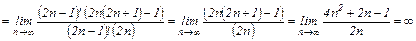
II. пределы функций.

1.

2.

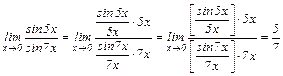
VI. Второй замечательный предел:

.

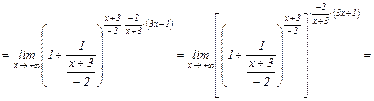
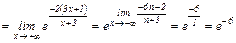VII. Односторонние пределы.

1. .

2. .

Пример 1.2.2. Найти производные указанных функций:

1) ,

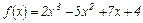2) ,

3) .

Решение.

1)

.

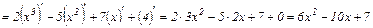2)

3) .

Пример 1.4.2. Найти предел, используя правило Лопиталя.

1)

2)

Решение.

1) .

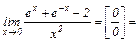
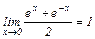2)

Пример 2.3.3. Вычислить приближенное значение .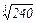

Решение.

1. Необходимо вычислить 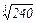, соответственно, рассмотрим функцию .

2. Так как , возьмём .

Применим Формулу (2.5.2) для рассматриваемой функции, сделав предварительные вычисления:

4. Таким образом, получаем

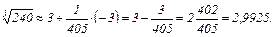
Пример 3.1.2. Найти точки экстремума для функции

Решение.

1. Найдём производную .

2. Найдём критические точки 1-го рода функции:

.

В нашем случае: .

3. Исследуем знак производной слева и справа от каждой критической точки и сделаем вывод о наличии точек экстремума:

.

.

4. Найдём экстремумы (экстремальные значения) функции:

.

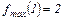Пример 3.1.3. Найти наибольшее и наименьшее значение функции на отрезке .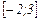

Решение.

1. Найдём производную .

2. Найдём критические точки .

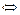
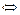
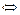
3. Найти значения функции в критических точках и на концах отрезка

; .

4. Из полученных трёх значений выбираем наибольшее и наименьшее.

; (Рис. 3.1.6).

Пример 3.2.1. Найти интервалы выпуклости и вогнутости, точки перегиба функции .

Решение.

1. Находим, что , а .

2. Критические точки 2-го рода: вторая производная существует на всей числовой оси; .

3. Отметим, что

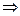т.е. функция вогнута на интервале , а

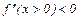
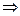т.е. функция выпукла на интервале .

Таким образом, точка является точкой перегиба.

4. Так как , то точка перегиба графика функции – (Рис. 3.2.1).

Пример 3.3.2. Найти асимптоты графика функции. .

Решение.

а) Вертикальные асимптоты ищутся среди точек разрыва, т.е. в нашем случае рассмотрим .

– вертикальная асимптота.

б) Исследуем поведение функции при , т.е. найдём наклонные (горизонтальные) асимптоты .

Соответственно,

Таким образом, имеется правая (при 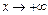) горизонтальная асимптота .

Пример 3.4.1. Исследовать функцию и построить её график.

Решение.

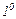. Область определения функции: , т.е. вся числовая ось.

. Исследуем функцию на чётность-нечётность, периодичность.

.

Таким образом, функция – чётная, следовательно, график функции симметричен относительно оси . Не периодическая.

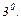Найдём вертикальные асимптоты. Исследуем поведение функции на бесконечности, найдём наклонные (горизонтальные) асимптоты.

а) Вертикальных асимптот нет, так как нет точек разрыва.

б) Исследуем поведение функции на бесконечности, найдём наклонные (горизонтальные) асимптоты .

Так как функция – четная, то исследуем поведение функции одновременно при .

Соответственно,

.

Следовательно, мы имеем , т.е. при 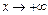так и при функция имеет одну и ту же горизонтальную асимптоту .

Исследуем функцию по нулевой производной, т.е. найдём интервалы знакопостоянства.

Исследуем функцию по первой производной, т.е. найдём точки экстремума функции и интервалы возрастания и убывания.

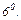Исследуем функцию по второй производной, т.е. найдём точки перегиба графика функции и интервалы выпуклости и вогнутости. .

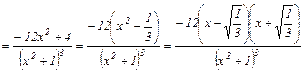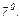Таблица.

Для удобства, сведём накопленную информацию в таблицу:

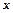
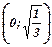
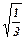
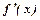
	возрастает
вогнута		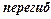выпукла

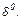График.

Используя таблицу, строим график функции (Рис. 3.4.1).

Пример 3.4.2. Исследовать функцию и построить её график.

Решение.

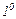. Область определения функции: .

. Исследуем функцию на чётность-нечётность, периодичность. ,

Не периодическая.

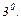Найдём вертикальные асимптоты. Исследуем поведение функции на бесконечности, найдём наклонные (горизонтальные) асимптоты.

а) Вертикальные асимптоты ищутся среди точек разрыва, т.е. в нашем случае рассмотрим

вертикальная асимптота.

б) Исследуем поведение функции на бесконечности, найдём наклонные (горизонтальные) асимптоты . ,

.

Следовательно, при мы имеем наклонную асимптоту .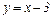

Исследование по нулевой производной, т.е. найдём интервалы знакопостоянства.

Исследование по первой производной, т.е. найдём точки экстремума функции и интервалы возрастания и убывания.

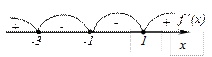
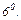Исследование по второй производной, т.е. найдём точки перегиба графика функции и интервалы выпуклости и вогнутости.

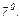Таблица.

Для удобства, сведём накопленную информацию в таблицу:

				Не существует
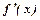
возрастает		убывает	убывает		возрастает
выпукла	вогнута

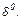График.

Используя таблицу, строим график функции (Рис.3.4.2).

Не нашли, что искали? Воспользуйтесь поиском: