
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ПО РАЗДЕЛУ МАТЕМАТИКИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«МОСКОВСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ ВЕТЕРИНАРНОЙ МЕДИЦИНЫ И БИОТЕХНОЛОГИИ ИМ. К.И. СКРЯБИНА»
_______________________________________________________________
Джугели Т.П., Кишкинова О.А., Кутликова И.В., Федькина Т.В.
Методические указания для решения контрольной работы
ПО РАЗДЕЛУ МАТЕМАТИКИ
«ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ»
(для студентов ветеринарно-биологического факультета)
Москва 2010
Данная контрольная работа должна позволить и студенту, и преподавателю оценить уровень усвоения указанной темы. Работа рассчитана на два академических часа и выполняется самостоятельно. В каждом варианте 7 заданий.Выполнение заданий №1, №2, №4 предполагает знание основных правил дифференцирования и правила дифференцирования сложных функций с помощью таблицы производных.
Основные правила дифференцирования таковы:
Пусть  и
и  - дифференцируемые функции. Тогда
- дифференцируемые функции. Тогда
1) 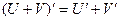 2)
2) 
3)  ,
,  4)
4)  , где C – const.
, где C – const.
Для эффективного дифференцирования сложных функций полезна таблица основных элементарных функций, аргумент которых есть тоже функция. Итак, пусть  , где
, где  . Тогда
. Тогда
1.  , C – const , C – const
| 2.  , n – const , n – const
|
3. 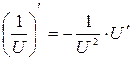
| 4. 
|
5. 
| 6. 
|
7. 
| 8. 
|
9. 
| 10. 
|
11. 
| 12. 
|
13.  , ,  , ,  ,
a – const ,
a – const
| 14. 
|
15.  , ,  , ,  ,
a – const ,
a – const
| 16. 
|
В задании №3 нужно найти производную третьего порядка согласно формулам:
 ,
,  .
.
Задания №5-№7 посвящены приложениям производной. В зависимости от номера варианта нужно уметь составить уравнение касательной к заданной кривой в заданной точке, вычислить приближенно некоторое арифметическое выражение с помощью формул приближенных вычислений, по закону движения точки найти её скорость и ускорение, найти предел функции в точке (предполагается знание правила Лопиталя).
Примерные варианты контрольной работы
Вариант-1.
Задание №1.
Найти производную и дифференциал:

Решение: с помощью формулы логарифмирования степени  , перепишем данную функцию в следующем виде:
, перепишем данную функцию в следующем виде:  , где
, где  .
.
По формуле  найдем производную данной функции.
найдем производную данной функции.
 [Производную дроби
[Производную дроби  находим по правилу дифференцирования
находим по правилу дифференцирования  ]
] 



 .
.
Дифференциал функции ищем по формуле:
 .
.

Ответ:  ;
; 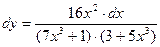 .
.
Задание №2.
Найти производную и дифференциал:
 .
.
Решение: для нахождения производной данной функции используем два правила дифференцирования: 1) 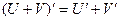 ;
;
2) 
 [справедливы следующие формулы:
[справедливы следующие формулы:  ]
] 
 .
.
Дифференциал функции ищем по формуле:
 .
.
 .
.
Ответ:  ;
; 
Задание №3.
Найти  -?
-?

Решение: найдем  от данной функции. Воспользуемся формулой:
от данной функции. Воспользуемся формулой:
 .
.
 .
.
Найдем 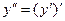
 .
.
Теперь найдем  .
.
 .
.
Ответ:  .
.
Задание №4.
Доказать, что  .
.
Для доказательства найдем производную в левой части равенства. Воспользуемся следующим правилом дифференцирования: 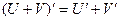 , т.е.
, т.е. 



 .
.
Получим, что левая часть равна правой.
Что и следовало доказать.
Задание №5.
Точка совершает прямолинейное колебательное движение по закону  ,
, 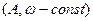 . Определить скорость и ускорение движения в момент времени
. Определить скорость и ускорение движения в момент времени  .
.
Решение:
 ;
; 


Ответ:  ;
;  .
.
Задание №6.
Вычислить приближенно: 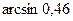 .
.
Решение: для приближенного вычисления будем использовать формулу:
 (*)
(*)
В нашем случае следует взять  . Выберем
. Выберем 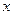 и
и  так, чтобы
так, чтобы  вычислялось легко, а
вычислялось легко, а  было достаточно мало по модулю. Например, x = 0,5
было достаточно мало по модулю. Например, x = 0,5  .
.
Подставим эти значения в формулу (*):

Ответ:  .
.
Задание №7.
Найти:  .
.
Решение:  [Воспользуемся правилом Лопиталя:
[Воспользуемся правилом Лопиталя:  ]=
]= 

Ответ:  .
.
Вариант - 2.
Задание №1.
Найти производную и дифференциал:

Решение: с помощью формулы логарифмирования степени 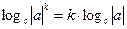 , перепишем данную функцию в следующем виде:
, перепишем данную функцию в следующем виде:  , где
, где  .
.
По формуле  найдем производную данной функции.
найдем производную данной функции.
 [производная дроби
[производная дроби  находим по правилу дифференцирования
находим по правилу дифференцирования  ]
] 
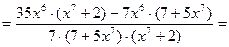

 =
=  .
.
Дифференциал функции ищем по формуле:


Ответ:  ;
; 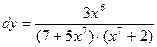 .
.
Задание №2.
Найти производную и дифференциал:
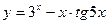
Решение: для нахождения производной данной функции используем два правила дифференцирования: 1) 
2) 
 [справедливы следующие формулы:
[справедливы следующие формулы: 

 .
.
Дифференциал функции ищем по формуле:

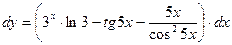
Ответ: 
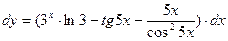
Задание №3.
Найти: 

Решение: найдем  от данной функции, используя формулу
от данной функции, используя формулу  и правило дифференцирования
и правило дифференцирования 
 .
.
Найдем  .
.
 .
.
Теперь найдем 

Ответ:  .
.
Задание №4.
Определить: 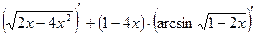
Решение:
1). Найдем  по формуле
по формуле 


2). Воспользовавшись формулой  , найдем производную функции
, найдем производную функции  .
.
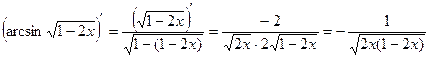
3). 
4). 
Получили, что  .
.
Что и требовалось доказать.
Задание №5.
Составить уравнение касательных к параболе  в точках с ординатой равной 1.
в точках с ординатой равной 1.
Решение: запишем уравнение касательной  .
.
В нашем случае  .
.
Для нахождения  , подставим значение
, подставим значение  в заданную функцию.
в заданную функцию.



Получили две точки:  .
.

Ответ:  .
.
Задание №6.
Вычислить приближенно: 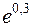
Решение: Для приближенного вычисления будем использовать формулу:


В нашем случае следует взять  ,
,  ,
,  . Выберем
. Выберем 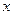 и
и  так, чтобы вычислялось легко, а
так, чтобы вычислялось легко, а  было достаточно мало по модулю. Например,
было достаточно мало по модулю. Например,  .
.
Подставим эти значения в формулу  :
:

Ответ: 
Задание №7.
Найти: 
Решение:  = [Воспользуемся правилом Лопиталя:
= [Воспользуемся правилом Лопиталя: 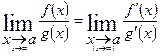 ]=
]= 


 .
.
Ответ: 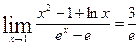 .
.
Вариант-3.
Задание №1.
Найти производную и дифференциал:

Решение: с помощью формулы логарифмирования степени  , перепишем данную функцию в следующем виде:
, перепишем данную функцию в следующем виде:  , где
, где  .
.
По формуле  найдем производную данной функции.
найдем производную данной функции.
 [производную дроби
[производную дроби  находим по правилу дифференцирования
находим по правилу дифференцирования  ]=
]= 
= 


 .
.
Дифференциал функции ищем по формуле:


Ответ:  ;
;  .
.
Задание №2.
Найти производную и дифференциал:
 .
.
Решение: для нахождения производной данной функции используем два правила дифференцирования:
1) 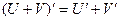 ;
;
2) 
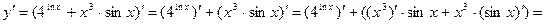
=[справедливы следующие формулы: 
 ;
;  ]= =
]= =  .
.
Дифференциал функции ищем по формуле:


Ответ:  ;
;  .
.
Задание №3
. Найти  -?
-?

Решение: найдем  от данной функции. Воспользуемся формулой
от данной функции. Воспользуемся формулой
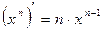 .
.



Найдем 

Теперь найдем 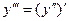 .
.
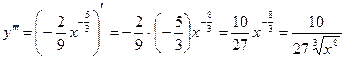
Ответ:  .
.
Задание №4.
Доказать, что  .
.
Для доказательства найдем производную в левой части равенства. Воспользуемся следующим правилом дифференцирования:  , т.е.
, т.е. 










Получаем, что левая часть равна правой.
Что и требовалось доказать.
Задание №5.
Тело движется прямолинейно по закону  . Найти скорость и ускорение движения в конце 1-ой секунды.
. Найти скорость и ускорение движения в конце 1-ой секунды.
Решение:
 ;
; 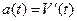

Т.к. в нашем случае 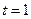 , то
, то
 .
.


Ответ:  ;
;  .
.
Задание №6.
Вычислить приближенно 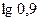 .
.
Решение: для приближенного вычисления будем использовать формулу:
 (*).
(*).
В нашем случае следует взять 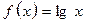 ;
;  ;
;  . Выберем
. Выберем 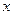 и
и  так, чтобы
так, чтобы  вычислялось легко, а
вычислялось легко, а  было достаточно мало по модулю. Например,
было достаточно мало по модулю. Например, 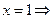
 .
.
Подставим эти значения в формулу (*):
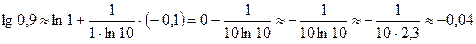
Ответ:  .
.
Задание №7.
Найти: 
Решение: 
 =[Воспользуемся правилом Лопиталя:
=[Воспользуемся правилом Лопиталя:  ]=
]= 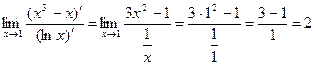
Ответ: 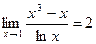 .
.
Дополнительно можно воспользоваться следующей литературой.
1. Задачи и упражнения по математическому анализу для ВТУЗов. Под редакцией Б.П. Демидовича.
2. Т.П. Джугели, В.П. Моисеенко, Л.Г. Кудинова. Высшая математика. Методические указания и контрольные задания. М.:МГАВМ и Б им. К.И. Скрябина, 2006г.
3. Т.П. Джугели, В.П. Моисеенко, Т.В. Федькина. Функции нескольких переменных. Учебно-методические указания. М.: ФГОУ ВПО МГАВМ и Б им. К.И.Скрябина, 2004г.
| <== предыдущая лекция | | | следующая лекция ==> |
| Статья 68. Председатель Дисциплинарного органа. | | | Андрей Руденко, 12 лет |
Не нашли, что искали? Воспользуйтесь поиском: