Статистические оценки параметров распределения

Смысл статистических методов заключается в том, чтобы по выборке ограниченного объема , т.е. по некоторой части генеральной совокупности, высказать обоснованное суждение об ее свойствах в целом.

Числовые значения, характеризующие генеральную совокупность, называются параметрами.

Одна из задач математической статистики – определение параметров большого массива по исследованию его части.

Опр. Статистической оценкой неизвестного параметра теоретического распределения называют его приближенное значение, зависящее от данной выборки , т.е. некоторую функцию этих величин

Здесь - значения признака,

-соответствующие частоты.

Статистическая оценка является случайной величиной.

Статистические оценки могут быть точечными и интервальными.

Опр. Величину называют точностью оценки. Чем меньше ,тем точнее определен неизвестный параметр.

Для того, чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определенным требованиям.

Чтобы оценка имела практическое значение, она не должна содержать систематической ошибки и иметь возможно меньшую дисперсию. Кроме того, при увеличении объема выборки вероятность сколь угодно малых отклонений должна быть близка к 1.

Опр. Оценка параметра называется несмещенной, если ее математическое ожидание равно оцениваемому параметру , при любом объеме выборки, т.е. , и смещенной, если .

Опр. Оценка называется эффективной, если при заданном она имеет наименьшую возможную дисперсию.

При рассмотрении выборок большого объема ( - велико) к статистическим оценкам предъявляется требование состоятельности.

Опр. Оценка называется состоятельной, если при увеличении объема выборки она стремится по вероятности к оцениваемому параметру.

Если оценка состоятельна, то практически достоверно, что при достаточно большом n .

Теорема. Несмещенной, состоятельной и эффективной оценкой генеральной средней (математического ожидания) служит выборочная средняя, , где - варианта выборки, - частота встречаемой варианты , - объем выборки.

Теорема. Смещенной оценкой генеральной дисперсии служит выборочная дисперсия: D_В = .

Эта оценка является смещенной, т.к.

. (7)

Т.е. выборочная дисперсия «занижает» генеральную дисперсию, т.к. . Положение можно «исправить», если ввести поправку в виде коэффициента , домножив на нее выборочную дисперсию .

Теорема. Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия:

. (8)

2. Интервальная оценка. Доверительный интервал.

При выборе малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т.е. приводит к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.

Определение. Интервальной оценкой параметра Θ называется числовой интервал, который с заданной вероятностью γ накрывает неизвестное значение параметра Θ.

Т.о. интервальная оценка определяется двумя числами – концами интервала, накрывающего оцениваемый параметр с заданной вероятностью.

Интервальные оценки позволяют установить точность и надежность оценок.

Пусть найденная по данным выборки статистическая характеристика служит оценкой неизвестного параметра . Чем меньше абсолютная величина разности , тем лучше, точнее определен неизвестный параметр.

Если и , то чем меньше , тем точнее оценка. Таким образом, положительное число характеризует точность оценки.

Однако статистические методы не позволяют категорически утверждать, что оценка удовлетворяет неравенству , можно лишь говорить о вероятности , с которой это неравенство выполняется.

Опр. Надежностью (доверительной вероятностью) оценки параметра по известному , называют вероятность выполнения неравенства ,т.е. .

Обычно надежность оценки задается наперед, причем, в качестве берут число, близкое к единице. Наиболее часто задают надежность, равную: 0,95; 0,99; 0,999.

Рассмотрим неравенство , необходимо определить в каких пределах находится неизвестный параметр , т.к. , имеем:

Тогда можно записать в виде . (9)

Последнее соотношение следует понимать так: вероятность того, что интервал 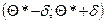заключает в себя (покрывает) неизвестный параметр , равна .

Опр. Доверительным интервалом называют интервал 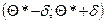, который покрывает неизвестный параметр с заданной точностью .

А. Доверительные интервалы для оценки математического ожидания нормального распределения при известном и неизвестном среднем квадратическом отклонении.

Пусть количественный признак генеральной совокупности распределен нормально и известно среднее квадратическое отклонение этого распределения. Как оценить неизвестное математическое ожидание (генеральная средняя ) по выборочной средней и найти доверительные интервалы, покрывающие параметр с надежностью .

Для решения этой задачи используют формулу

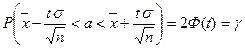. (10)

Смысл полученного соотношения таков: с надежностью можно утверждать, что доверительный интервал покрывает неизвестный параметр , причем, точность оценки . Число - определяется из равенства , по таблице функции Лапласа находят аргумент ,которому соответствует значение функции Лапласа, равное .

В большинстве случаев среднее квадратическое отклонение исследуемого признака - неизвестно. Поэтому, вместо при большой выборке применяют исправленное выборочное среднее квадратическое отклонение , являющееся оценкой . Доверительный интервал будет иметь вид: , а формула (10) примет вид: . (11)

Доверительный интервал зависит от объема выборки. Английский статистик Госсет (псевдоним Стьюдент) нашел доверительный интервал для оценки математического ожидания нормального распределения при неизвестном , зависящий от объема выборки и надежности , а именно: , где находят по таблице 4 по данным и . Рабочая формула: . (12)

Но при больших объемах выборок числа и (найденные по таблице 2 – значения функции Лапласа) практически совпадают.

Не нашли, что искали? Воспользуйтесь поиском: