Правило дифференцирования сложной функции.

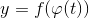6) Если функция имеет производную в точке , а функция имеет производную в точке , то сложная функция имеет производную в точке , причем .

Таблица производных основных функций

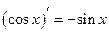
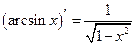
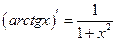
Первообразная. Неопределённый интеграл

Первообразная. Непрерывная функция F (x) называется первообразной для функции f (x) на промежутке X, если для каждого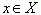

F’ (x) = f (x).

П р и м е р. Функция F (x) = x ³ является первообразной для функции

f (x) = 3 x ² на интервале (- 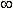, + 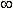), так как

F’ (x) = (x ³) ’ = 3 x ² = f (x) для всех x (- 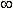, + 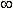). Легко проверить, что функция x ³ + 13 имеет ту же производную 3 x ², поэтому x ³ + 13 также является первообразной для функции 3 x ² для всех x (- 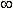, + 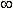). Ясно, что вместо 13 можно взять любую постоянную.

Таким образом, задача нахождения первообразной имеет бесчисленное множество решений. Этот факт нашёл отражение в определении неопределённого интеграла.

Неопределённый интеграл функции f (x) на промежутке X есть множество всех её первообразных. Это записывается в виде:

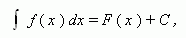
где C – любая постоянная, называемая постоянной интегрирования.

Основные свойства неопределённого интеграла

Если функция f (x) имеет первообразную на промежутке X, и k – число, то

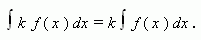
Т.е. постоянную можно выносить за знак интеграла.

Если функции f (x) и g (x) имеют первообразные на промежутке X, то

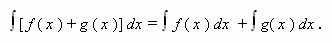
Т.е. интеграл суммы равен сумме интегралов.

Если функция f (x) имеет первообразную на промежутке X, то для внутренних точек этого промежутка:

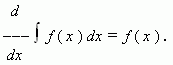
Т.е. производная от интеграла равна подынтегральной функции.

Если функция f (x) непрерывна на промежутке X и дифференцируема во внутренних точках этого промежутка, то:

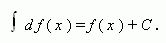
Т.е. интеграл от дифференциала функции равен этой функции плюс постоянная интегрирования.

Таблица основных интегралов

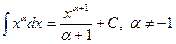
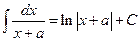
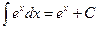
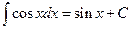
Определённый интеграл. Формула Ньютона – Лейбница

Рассмотрим непрерывную функцию y = f (x), заданную на отрезке [ a, b ] и сохраняющую на этом отрезке свой знак (рис.8).
Фигура, ограниченная графиком этой функции, отрезком [ a, b ] и прямыми x = a и x = b, называется криволинейной трапецией.
Для вычисления площадей криволинейных трапеций используется следующая теорема:

Если f – непрерывная, неотрицательная функция на отрезке [a, b], и F – её первообразная на этом отрезке, то площадь соответствующей криволинейной трапеции равна приращению первообразной на отрезке [a, b], т.e.

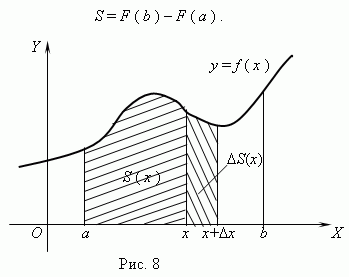
Рассмотрим функцию S (x), заданную на отрезке [ a, b ]. Если a<x b, то S (x) – площадь части криволинейной трапеции, лежащей слева от вертикальной прямой, проходящей через точку (x, 0). Отметим, что если x = a, то S (a) = 0, а S (b) = S (S – площадь всей криволинейной трапеции). Можно доказать, что

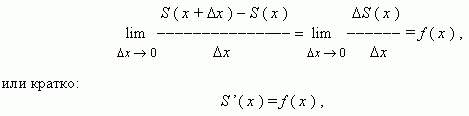
т.e. S (x) – первообразная для f (x). Отсюда, согласно основному свойству первообразных, для всех x [ a, b ] имеем:

S (x) = F (x) + C,

где C – некоторая постоянная, F – одна из первообразных функции f.

Чтобы найти C, подставим x = a:

F (a) + C = S (a) = 0,отсюда, C = - F (a) и S (x) = F (x) - F (a). Так как площадь криволинейной трапеции равна S (b), то подставляя x = b, получим:

S = S (b) = F (b) - F (a).

Основные свойства определённого интеграла

Пространство элементарных событий. Событие: невозможное, достоверное, случайное. Действия над событиями.     Под событием в теории вероятностей понимают любой факт, который может произойти или не произойти в результате опыта со случайным исходом. Самый простой результат такого опыта (например, появление "орла" или "решки" при бросании монеты, попадание в цель при стрельбе, появление туза при вынимании карты из колоды, случайное выпадение числа при бросании игральной кости и т.д.) называется элементарным событием. Множество всех элементарных событий Е называется пространством элементарных событий. Так, при бросании игральной кости это пространство состоит из шести элементарных событий, а при вынимании карты из колоды – из 52. Событие может состоять из одного или нескольких элементарных событий, например, появление двух тузов подряд при вынимании карты из колоды, или выпадение одного и того же числа при трёхкратном бросании игральной кости. Тогда можно определить событие как произвольное подмножество пространства элементарных событий. Достоверным событием называется всё пространство элементарных событий. Таким образом, достоверное событие – это событие, которое обязательно должно произойти в результате данного опыта. При бросании игральной кости таким событием является её падение на одну из граней. Невозможным событием () называется пустое подмножество пространства элементарных событий. То есть, невозможное событие не может произойти в результате данного опыта. Так, при бросании игральной кости невозможным событием является её падение на ребро. События А и В называются тождественными (А = В),если событие А происходит тогда и только тогда, когда происходит событие В.   Событие А' называется противоположным событию А, если не произошло событие А. Так, промах и попадание при стрельбе – противоположные события.   События А и В называются несовместными (А В = ), если их одновременное появление невозможно. Например, выпадение и "решки", и "орла" при бросании монеты. Если при проведении опыта могут произойти несколько событий и каждое из них по объективным условиям не является более возможным, чем другое, то такие события называются равновозможными. Примеры равновозможных событий: появление двойки, туза и валета при вынимании карты из колоды, выпадение любого из чисел от 1 до 6 при бросании игральной кости и т.п. Классическое определение вероятности. Пусть пространство элементарных событий Е состоит из N равновозможных элементарных событий, среди которых имеется n событий, благоприятствующих событию А, тогда число   Р (А) = n / N   называется вероятностью события А.   Основные свойства вероятности. Пусть задано пространство элементарных событий Е, а вероятности Р определены на событиях из Е. Тогда:

Условная вероятность. Независимость событий

Вероятность появления события А при условии, что событие В произошло, называется условной вероятностью события А и вычисляется по формуле:

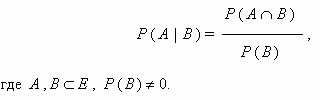
События А, В 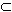Е называются независимыми, если Р (А В) = Р (А) · Р (В).

В противном случае события А и В называются зависимыми.

Случайные величины и функции распределения случайных величин.

Переменная величина называется случайной, если в результате опыта она может принимать действительные значения с определёнными вероятностями.

Случайная величина Х называется дискретной, если существует такая неотрицательная функция

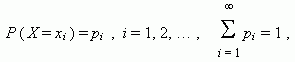
которая ставит в соответствие значению х_i переменной Х вероятность р_i, с которой она принимает это значение. Дискретные случайные величины X и Y называются независимыми, если события Х = х_i и Y = y_j при произвольных i и j являются независимыми.

Случайная величина Х называется непрерывной, если для любых a < b существует такая неотрицательная функция f (x), что

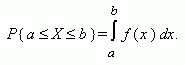
Функция f (x) называется плотностью распределения непрерывной случайной величины.

Вероятность того, что случайная величина Х принимает значение меньшее х, называется функцией распределения случайной величины Х и обозначается F (x):

F (x) = Р (X x).

Общие свойства функции распределения:

Характеристики случайных величин

Математическое ожидание.Свойства математического ожидания.

Дисперсия. Свойства дисперсии.Среднее квадратичное отклонение.

Математическим ожиданием дискретной случайной величины Х, принимающей конечное число значений х_i с вероятностями р_i, называется сумма:

М (Х) = х ₁ · р ₁ + х ₂ · р ₂ + х ₃ · р ₃ +... + х_n · р_n.

Свойства математического ожидания:

1) М (с · Х) = с · М (Х), c R,

2) М (Х + Y) = М (Х) + М (Y), Х, Y Е,

3) М (Х · Y) = М (Х) · М (Y) для независимых случайных величин Х и Y.

Дисперсией случайной величины Х называется число:

D (Х) = М { [ Х – М (Х)] ² }= М (Х ² ) – [ М (Х)] ².

Свойства дисперсии:

1) D (с · Х) = с ² · D (Х), c R,

2) D (Х + Y) = D (Х) + D (Y) для независимых случайных величин Х и Y.

Среднее квадратичное отклонение:

Нормальное (гауссово) распределение

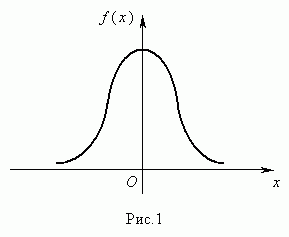
Случайная величина Х имеет нормальное (гауссово) распределение, если её плотность распределения определяется зависимостью:

При m = 0, = 1 нормальное распределение называется стандартным.

График плотности нормального распределения представлен на рис.1.

Математическая модель демографического процесса.

Одной из наиболее доступных для непосредственного измерения социальных величин является численность людей. Поэтому именно область демографии привлекает исследователей, давая надежды на успех в построении количественной теории. Примечательно, что и проникновение математических методов в биологию во многом проходило под флагом описания популяционной динамики животных.

Однако несмотря на измеримость данных и, более того, на очевидность формулы, вытекающей из закона сохранения и описывающей демографическую динамику:

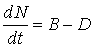, (1)

где N – число людей, B – число рождений и D – число смертей в единицу времени, на микроуровне оказывается, что и число рождений, и число смертей зависят от многих других социальных параметров, и в том числе от «человеческого фактора» – принятия решений отдельными людьми, слабо поддающегося формализации.

Кроме того, формула (1) не учитывает перемещения людей в пространстве, а следовательно она должна быть расширена:

,

где вектор J соответствует миграционному потоку. В этом случае задача еще больше усложняется, поскольку миграционные процессы еще сильнее подвержены влиянию внешних факторов.

Поэтому описание демографических процессов на микроуровне наталкивается на существенные проблемы, связанные, прежде всего, с неразработанностью формальных социальных законов, увязывающих экономические, политические, этические и прочие факторы, определяющие поведение малых групп людей.

Таким образом, единственным пока доступным подходом является макроописание, не вдающееся в мелкие детали демографического процесса и описывающее динамику больших людских масс, для которых влияние человеческого фактора заметно ниже.

Теорема (правило Лопиталя).

Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть или . Тогда, если существует предел отношения производных этих функций , то существует и предел отношения самих функций f(x)/g(x) при x → а, причем

(1)

Таким образом, коротко правило Лопиталя можно сформулировать следующимобразом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.

Пример:

.

Не нашли, что искали? Воспользуйтесь поиском: