Понятие модели и операции. Математические модели, исследование операций и численные методы в научных исследованиях в области спорта.

Приведенные выше примеры моделей-игрушек являются примерами физического моделирования, при котором те или иные свойства объекта изучаются на его уменьшенной (иногда, увеличенной) копии. Так, например, для того, чтобы оценить поведение самолета в воздухе при определенной скорости, его уменьшенную модель обдувают в аэродинамической трубе воздушным потоком, имеющим ту же скорость. Однако в наше время физическое моделирование, за редким исключением, потеряло смысл. Действительно, оно не позволяет получать в опережающем режиме времени информацию о динамике изменения свойств объекта с течением времени, что необходимо знать при проектировании объекта для оптимизации его будущих эксплуатационных характеристик. (Заметим, что к изучению научно-методических задач в сфере физической культуры и спорта, в частности задач биомеханики, этот метод вообще не применим).

Другой разновидностью моделирования является информационное моделирование, которое имеет дело с информационными моделями. Примерами информационных моделей могут служить видеоматериалы, графики, таблицы, формулы, уравнения и т.д. В научных исследованиях в подавляющем большинстве случаев используются информационные модели, обеспечивающие применение количественных методов исследования, то есть, математические модели. Математическое моделирование позволяет изучать самые разнообразные объекты и решать сопутствующие этому изучению задачи. Нас же интересуют живые объекты, решающие двигательные задачи, то есть поступающие целенаправленно. Целенаправленность действий вообще является одним из характерных признаков, отличающих живое от неживого. Научные методы, ориентированные на организацию и исследование целенаправленных систем, получили общее название «исследование операций». Почему именно такое название?

Дело в том, что под операцией понимают всякое мероприятие (систему действий), объединенное единым замыслом и направленное к достижению какой-то цели.

Для оценки возможностей использования методов и идей исследования операций применительно к задачам физического воспитания и спорта напомним и поясним некоторые термины и понятия этой дисциплины.

1) Операция является управляемым мероприятием, и параметры, характеризующие ее организацию, выбираются так, чтобы по возможности наилучшим образом способствовать достижению поставленной цели. При этом в понятие «организация» включается и набор технических средств, используемых в операции. Решение о проведении (или не проведении) операции принимает оперирующая сторона, то есть лица, заинтересованные в проведении операции и располагающие необходимой для ее исследования информацией. Исследователь операции сообщает оперирующей стороне результаты проведенного им на основании полученной информации исследования.

2) Для того, чтобы применить к оценке операции количественные методы, операцию надо формализовать, т.е. построить ее математическую модель. Эта модель должна отражать все существенные черты операции, все факторы, от которых зависит успех операции. Вместе с тем модель должна быть по возможности простой, свободной от второстепенных факторов, усложняющих модель и делающих результаты исследования трудно воспринимаемыми.

Все величины, входящие в модель, можно подразделить на три группы. К первой группе относятся эндогенные (их называют также фазовыми) переменные. Они определяют состояние операции на данный момент времени. Эндогенные переменные (греч. Ендо – внутрь) должны определяться из самой модели операции. Ко второй группе относятся экзогенные переменные (греч. Экзо – наружу). Эти переменные являются внешними по отношению к модели, т.е. не определяются из модели, а тем или иным способом задаются извне. И, наконец, к третьей группе относятся управления – переменные, значения которых задаются оперирующей стороной Как и экзогенные переменные, они являются внешними по отношению к модели, но значения экзогенных величин не зависят от оперирующей стороны.

3) Всякий конкретный выбор параметров, зависящих от нас, называется решением. Для сравнения решений между собой выбирается количественный критерий, отражающий целевую направленность операции (показатель эффективности операции, или целевая функция).

Решения называются оптимальными, если они по тем или иным признакам предпочтительнее других.

Математическая модель операции не определяется однозначно описанием операции, так как построение модели является искусством: именно, от составителя модели зависит, какие факторы считать существенными, а какие второстепенными. Поэтому полезно использовать несколько моделей и сравнивать результаты, полученные по разным моделям, для того, чтобы определить, какая из них более адекватна действительности. Проводимая таким образом процедура в численных методах (см. ниже) называется вычислительным экспериментом

Создание математической модели является самым важным и ответственным этапом исследования, требующим, в первую очередь, глубокого знания существа моделируемого явления, и, кроме того, хорошего владения математическим аппаратом. Поэтому наилучшие модели создаются специалистами в области проводимого исследования, владеющими необходимыми математическим методами, или коллективами, в которые входят и специалисты данной области, и математики.

Вместе с тем, не следует ставить знак равенства между исследованием операций и математическим моделированием, рассматривая их как две стороны одной и той же медали. Исследование операций невозможно без построения математических моделей, но математические модели можно строить не только для операций, но и для естественных (нецеленаправленных) явлений.

Как уже отмечалось, математическое моделирование обеспечивает возможность применения количественных методов исследования. Используя построенную математическую модель изучаемого явления, можно по каким-то приближенным исходным данным, полученным, скажем, в результате измерений, получить в результате вычислений опять-таки приближенные численные значения интересующих нас характеристик явления.

Методы приближенного решения математических задач получили название численных (вычислительных) методов. Одна из важных проблем численных методов – проблема точности полученного результата. Естественно, что при работе с исходными приближенными данными полученный результат тем более будет приближенным и не более точным, чем исходные данные.

Величина, характеризующая точность результата, называется его погрешностью.

. Есть четыре источника погрешности результата:

1. математическая модель;

2. исходные данные;

3. погрешности метода;

4. погрешность вычислений (возникающая из-за округлений).

Построение математической модели связано с упрощением исходного явления и недостаточно точным заданием входных данных. По отношению к численному методу, реализующему данную модель, погрешности построения модели и входных данных являются неустранимыми. Погрешность метода связана с тем, что точные операторы и исходные данные заменяются приближенными, ее целесообразно выбирать так, чтобы она была в 2-5 раз меньше неустранимой погрешности. Большая погрешность снижает точность ответа, а заметно меньшая – невыгодна, т.к. она требует увеличения объема вычислений. При рассмотрении неустранимой погрешности выделяют понятия абсолютной и относительно й погрешностей.

Пусть X – точное значение величины, а X ⃰ – ее приближенное значение.

Абсолютной погрешностью числа X ⃰ называется величина ΔX ⃰, удовлетворяющая условию X ⃰ 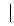≤ ΔX ⃰. Относительной погрешностью называется некоторая величина δ X ⃰, удовлетворяющая условию
≤ δX ⃰

Рассмотрим следующий пример.

При измерении длины комнаты, при подлинном значении измеряемой величины, равном 6 м, получен результат 5,8 м. Таким образом, ошибка составила 0,2 м. С такой же ошибкой была измерена длина 9-километрового проспекта Победителей. Что можно сказать о точности этих двух измерений?

Очевидно, что точность результата лучше характеризует его относительная погрешность. В нашем примере абсолютная погрешность одна и та же в обоих измерениях, а относительные погрешности 1/29 и 1/45000, соответственно. Ясно что измерение проспекта выполнено несравнимо точнее.

Не нашли, что искали? Воспользуйтесь поиском: