УСОВЕРШЕНСТВОВАННЫЙ МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ

Рассмотрим снова рис. 1. Нетрудно заметить, что, хотя каждое последующее значение х_п находится ближе к решению уравнения, чем предшествующее, все они сильно отличаются от а. По-видимому, можно было бы добиться более быстрой сходимости метода, если при каждой очередной

Рис. 5. Геометрическое представление усовершенствованного метода последовательных приближений для 0 < f'(x) < 1.

итерации делать большую поправку к очередному значению х_п. Иначе говоря, можно принять следующую формулу для х_n+1:

,

где а > 1.

Эта идея поясняется на рис. 5, где в увеличенном виде изображена небольшая часть рис. 1. Наилучшим выбором ее следует признать тот, что изображен на рисунке, так как тогда х_п+1 получается равным а. Попытаемся определить это наилучшее значение α.

Заметим, что расстояние между х_п+1 и а равно , и так как у= х есть прямая линия, идущая под углом 45° к осям координат, расстояние между f(a) и f(x_n) также равно . Поэтому тангенс угла θ равен

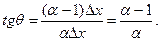(7)

С другой стороны,

(8)

и, используя теорему о среднем значении,

где .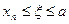

Из (7) и (8) получаем значение α в виде

(9)

Значение ξ, конечно, остается неизвестным, но для значения /'(^) можно принять следующее приближение:

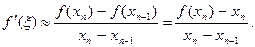(10)

Геометрически процесс отыскания следующего приближения, х_п+1, сводится к тому, что проводится хорда между точками и 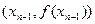, и определяется точка ее пересечения с прямой у = х.

Формула итерационного метода приобретает при этом следующий вид:

(11)

где α определяется по формулам (9) и (10).

Возникает вопрос, как это усовершенствование влияет на сходимость метода. Из формулы (9) видно, что при должно получиться . Этот случай изображен на рис. 1, где последовательные поправки были слишком малы; так как α > 1, усовершенствованный метод увеличит эти поправки и ускорит сходимость вычислений.

При имеем 1/2 < α < 1. Этот случай изображен на рис. 2, где каждая поправка также была слишком велика. В усовершенствованном методе все поправки уменьшаются на коэффициент, расположенный между 1/2 и 1; сходимость метода при этом, естественно; также улучшается.

Более важны случаи, когда простой метод последовательных приближений расходится. Если f'(х)<1, то α < 0. Как показано на рис. 3, каждая очередная поправка имеет неправильный знак и соответствующее приближение отстоит от а дальше, чем предыдущее. Так как, α для этого случая отрицательно, то в усовершенствованном методе знаки поправок изменяются нужным образом.

Наконец, при имеем 0 < α < 1/2. В этом случае, как показано на рис. 4, поправки были слишком велики; при усовершенствованном методе каждая поправка умножается на коэффициент, расположенный между 0 и 1/2. Естественно, что уменьшение поправок должно быть в этом случае более резким, чем на рис..2, где приближения сходятся, в то время как на рис. 4 они расходятся.

Небольшая дальнейшая модификация метода последовательных приближений приводит к одному из наиболее известных численных методов — к методу Ньютона - Рафсона для нахождения корней уравнения. Однако в некоторых случаях методы, описанные выше, предпочтительнее метода Ньютона - Рафсона.

Не нашли, что искали? Воспользуйтесь поиском: