Практическая работа № 12

Тема: Многогранники.

Цель: Знать формулы вычисления боковой и полной поверхности призмы. пирамиды, параллелепипеда и уметь применять их к решению задач.

Методические рекомендации

Площадью поверхности многогранника по определению считается сумма площадей, входящих в эту поверхность многоугольников.

Основные формулы

№ п/п	Наименование многогранника	Изображение	Площадь боковой и полной поверхности
1.	Куб		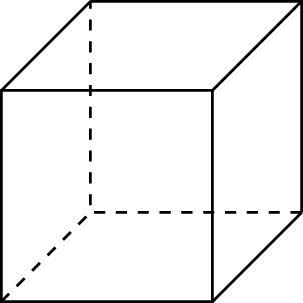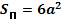V=a3
2.	Прямоугольный параллелепипед		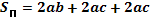V=a*b*c V=Sосн*h
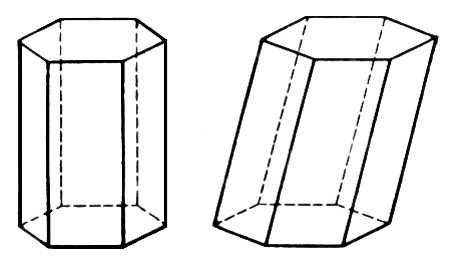
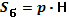
3.	Призма		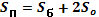V=Sосн*h
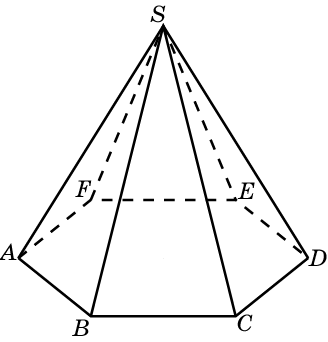
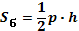
4.	Пирамида		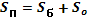V=(1/3)*Sосн*h

Варианты заданий практической работы

1 вариант

1. Основанием прямой призмы ABCDA₁B₁C₁D₁ является параллелограмм ABCD со сторонами 6 см и 12 см и углом 60°. Диагональ B₁D призмы образует с плоскостью основания угол в 30°. Найдите площадь полной поверхности призмы.

2. Сторона основания правильной треугольной пирамиды равна 3 см, а угол между боковой гранью и основанием равен 45°. Найдите площадь полной поверхности пирамиды.

3. Сторона основания правильной треугольной пирамиды равна а, а боковая грань наклонена к плоскости основания под углом a. Найдите площадь полной поверхности пирамиды.

2 вариант

1. Основанием прямой призмы ABCDA₁B₁C₁D₁ является параллелограмм ABCD со сторонами 4 см и 4 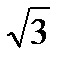см и углом 30°. Диагональ AC₁ призмы образует с плоскостью основания угол в 60°. Найдите площадь полной поверхности призмы.

2. Высота основания правильной треугольной пирамиды равна 3 см, а угол между боковой гранью и основанием пирамиды равен 45°. Найдите площадь полной поверхности пирамиды.

3. Основание пирамиды – квадрат со стороной а. Одна из боковых граней перпендикулярна основанию, а две смежные с ней грани составляют с плоскостью основания угол a. Найдите площадь полной поверхности пирамиды.

3 вариант

1. Основанием прямой призмы ABCDA₁B₁C₁D₁ является параллелограмм ABCD со сторонами 6 см и 6 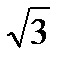см и углом 150°. Диагональ B₁D призмы образует с плоскостью основания угол в 60°. Найдите площадь полной поверхности призмы.

2. Сторона правильной треугольной пирамиды равна 4 см, а угол между боковым ребром и основанием равен 60°. Найдите площадь полной поверхности пирамиды.

3. Высота правильной четырехугольной пирамиды равна H, а боковое ребро составляет с основанием угол a. Найдите площадь полной поверхности пирамиды.

4 вариант

1. Основанием прямой призмы ABCDA₁B₁C₁D₁ является параллелограмм ABCD со сторонами 3 см и 6 см и углом 120°. Диагональ AC₁ призмы образует с плоскостью основания угол в 30°. Найдите площадь полной поверхности призмы.

2. Высота основания правильной треугольной пирамиды равна 4 см, а угол между боковым ребром и основанием пирамиды равен 30°. Найдите площадь полной поверхности пирамиды.

3. Основание прямоугольного параллелепипеда – квадрат. Угол между диагоналями смежных граней, исходящих из одной вершины, равен a. Диагональ параллелепипеда равна d. Найдите площадь полной поверхности параллелепипеда.

Не нашли, что искали? Воспользуйтесь поиском: