Лекция 8 Скалярное, векторное и смешанное произведение векторов

ИКТИБ ИТА ЮФУ

КУРС ЛЕКЦИЙ ПО МАТЕМАТИКЕ

Лекция 8 Скалярное, векторное и смешанное произведение векторов

Что главное мы узнали на прошлой лекции

На прошлой лекции мы изучали в основном линейные свойства векторов, приступив к изучению скалярного произведения векторов.

Что мы узнаем на этой лекции

На текущей лекции мы изучим скалярной, векторное, смешанное произведение векторов.

1. Вычисление скалярного произведения
в декартовой системе координат

Теорема 1. В декартовой системе координат скалярное произведение геометрических векторов равно сумме попарных произведений их координат.

Доказательство. Рассмотрим скалярное произведение векторов и , заданных в декартовой системе координат . Используя свойства скалярного произведения векторов, запишем следующие преобразования:

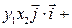
Мы использовали тот факт, что скалярное произведение различных, взаимно перпендикулярных, базисных векторов равно 0. В то же время скалярное произведение одинаковых базисных векторов единичной длины равно 1. Теорема доказана.

Не нашли, что искали? Воспользуйтесь поиском: