Пример построения геометрии двумерной области в виде буквы R

Рассмотрим двумерную область в виде латинской буквы «R». Геометрия области, отнесенной к декартовой системе координат , показана на рис. 1. Размеры буквы определяются следующими параметрами: HL=1.4 (высота); WL=0.8 (ширина); WWL=0.2 (ширина стенок); HAL=0.7 (дополнительный размер по высоте).

Заметим, что при задании входных параметров задачи нужно заботиться об их согласованности по системам единиц. Пусть выбрана система единиц – СИ, и, таким образом, геометрические размеры даются в метрах.

Рис. 1. Рис. 2.

Будем строить сначала твердотельную модель, а затем, из нее – конечно-элементную. Твердотельную модель получим методом построения геометрических объектов «снизу – вверх». Для этого сначала построим опорные точки, потом – линии, и, наконец, двумерные области.

Нам понадобится сначала построить две односвязные области: первую область, ограниченную внешними линиями буквы «R», и вторую область, ограниченную внутренними линиями. Затем, с использованием булевской операции вычитания геометрических областей (команда ASBA) можно будет получить итоговую область буквы «R» с отверстием.

Анализируя вид буквы «R», замечаем, что ее правая верхняя часть ограничена кривыми линиями, которые можно задавать отрезками эллипсов. Центр эллипсов будет совпадать с центров декартовой системы координат , сдвинутой относительно исходной системы координат на WWL вправо по оси абсцисс, и на (HL-HAL/2) вверх по оси ординат. Для внешней криволинейной части отношение полуосей эллипса по оcям 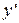и равно: =(HAL/2)/(WL-WWL). Поэтому, для дальнейшего построения криволинейных линий удобно определить новую эллиптическую систему координат под номером 11, введя команды:

PEL=(HAL/2)/(WL-WWL)! Параметр эллиптичности для криволинейной части фигуры

LOCAL,11,1,WWL,HL-HAL/2,,,,,PEL! Эллиптическая система координат 11

CSYS,0! Переход в основную декартову систему координат

Теперь создаем область, ограниченную внешними линиями буквы «R». Сначала создаем девять опорных точек:

! Определение основных опорных точек для внешней границы

K,1,0,0

K,2,WWL,0

K,3,WWL,HL-HAL-WWL

K,4,WL-WWL,0

K,5,WL,0

K,6,WWL,HL-HAL

K,7,WL,HL-HAL/2

K,8,WWL,HL

K,9,0,HL

Затем определяем линии по точкам. При этом для создания эллиптической линии просто переходим в эллиптическую систему координат, и в ней проводим «прямую» линию, которая в результате оказывается дугой эллипса. Команда AL в итоге позволяет создать нужную нам первую область A1:

! создание линий по точкам

L,1,2 $ L,2,3 $ L,3,4 $ L,4,5 $ L,5,6

CSYS,11! Переход в систему координат с номером 11

L,6,7 $ L,7,8

CSYS,0! Переход в основную декартову систему координат

L,8,9 $ L,9,1

AL,1,2,3,4,5,6,7,8,9! Определение площади 1 по линиям

Замечание. Область A1 можно было создать и по команде

A,1,2,3,4,5,6,7,8,9! Определение площади 1 по опорным точкам

Действительно, эта команда создает площадь (поверхность) по опорным точкам с проведением прямых линий между точками. Однако если между токами уже определены линии, то команда A использует их, и в результате оказывается эквивалентной команде AL.

Создавая другие области, нужно иметь в виду, что команда AL в командном режиме строит область максимум по десяти линиям, а команда A – максимум по восемнадцати точкам (если не используется значение ALL для первого поля). В интерактивном графическом режиме таких ограничений нет. Но если есть желание работать только в командном режиме с использованием APDL, то можно разбить сложную область на более простые подчасти с числом точек или линий, удовлетворяющих ограничениям команд A или AL. Создав эти подобласти, нужную сложную область можно получить объединением подобластей. Можно их и не объединять в одну область, но тогда нужно проследить, чтобы граничащие подобласти имели одни и те же опорные точки и линии на соседствующих границах.

Действуя аналогично, построим вторую область – пустотелую часть буквы «R»:

! Определение отверстия - площади 2

K,10,WWL,HL-HAL/2-(WL-2*WWL)*PEL

K,11,WL-WWL,HL-HAL/2

K,12,WWL,HL-HAL/2+(WL-2*WWL)*PEL

CSYS,11

L,10,11 $ L,11,12

CSYS,0

L,12,10

AL,10,11,12

Теперь булевская операция вычитание позволяет из первой области вырезать вторую, и в результате получить требуемую область с отверстием, причем эта область будет иметь номер 3:

ASBA,1,2! Вырезать из области 1 область 2

В итоге создана двумерная твердотельная модель без граничных условий.

Не нашли, что искали? Воспользуйтесь поиском: