Последовательность действий 3 страница

2. Значением каждого элемента целочисленного массива X из n элементов (n < = 30) является дополнение его порядкового номера до 100. Сформировать и вывести на экран этот массив.

3. Дан массив Х из k элементов, k= 22. Получить массив Y, каждый элемент которого определяется формулой .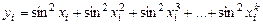

Вариант 18

1. Дан массив {a_i}, i = 1,…20. Найти

2. Даны целые числа X и Y и массив Z из n элементов (n < = 40). Вычислить сумму элементов массива, для которых выполняется условие x<z_i<y.

3. Дан целочисленный массив А из k элементов(k < = 30). Пусть m – наибольшее, а n – наименьшее из a ₁, …., a_k. Получить в порядке возрастания все целые числа из интервала (n,m), которые не входят в последовательность a ₁, …., a_{k .}

Вариант 19

1. Даны целые числа a ₁, …, a ₃₀. Получить новую последовательность, выбросив из исходной максимальное число.

2. Дан массив вещественных чисел X из 40 элементов. Определить количество элементов массива, отличающихся от среднего арифметического значения элементов этого массива не более чем на 2.

3. Дан массив целых чисел a ₁, …., a_n (n 30). Для каждого из чисел выяснить, сколько раз оно входит в этот массив. При выводе не допускается повторно указывать число вхождений для чисел, встречающихся в последовательности несколько раз.

Вариант 20

1. Дан массив X из n элементов (n 22). Получить массив Z, в котором .

2. Дан массив вещественных чисел С из m элементов, m<= 40. Получить новый массив удалением из исходного массива всех отрицательных элементов.

3. Дан целочисленный массив Х, содержащий n элементов (n < = 30). Найти минимальный и максимальный элементы массива и упорядочить по убыванию элементы, расположенные между ними.

Вариант 21

1. В массиве X из n элементов (n 50) найти наибольший и второй по величине элементы заданного массива.

2. Дан массив Х из 22 элементов. Найти первый по порядку отрицательный и минимальный элементы массива (считать, что минимальный элемент в массиве один) и поменять их местами.

3. Дан целочисленный массив X из 30 элементов. Преобразовать массив так, чтобы в нем сначала располагались положительные элементы, затем нулевые, потом отрицательные в порядке их следования. Вспомогательный массив не использовать

Вариант 22

1. Даны действительные y ₁, …y_n (n 22). Выяснить, каких элементов в последовательности больше: положительных или отрицательных.

2. Дан массив Х из m элементов, m= 28. Найти два элемента, модуль разности которых имеет минимальное значение.

3. Выяснить, верно ли, что все члены последовательности {a_i} (i = 1,…,5) входят в последовательность {b_j} (j = 1,…,10).

Контрольные вопросы

1. Что такое массив?

2. Назовите основные характеристики (атрибуты) массива.

3. Как ввести и вывести массив?

4. Какого типа могут быть элементы массива?

5. Нужно ли указывать количество элементов в массиве при описании? Если да, то почему?

6. Какого типа может быть индекс в массиве?

7. Что может представлять собой индекс элемента в массиве?

8. Может ли индекс элемента в массиве принимать нулевое или отрицательное значение? Если да, то приведите пример описания такого массива.

9. Как обратиться к элементу массива?

10. Можно ли изменять количество элементов массива при выполнении программы?

11. Как поменять местами два элемента массива?

12. Что называется сортировкой массива? Какие методы сортировки Вы знаете?

13. В чем состоит метод попарно-обменной сортировки?

14. Объясните алгоритм сортировки методом выбора (метод поиска максимального или минимального элемента).

Лабораторная работа № 5

Двумерные массивы

Цель работы – освоить работу с матрицами, научиться организовывать циклы для обработки многомерных массивов.

Постановка задачи

Написать две программы согласно индивидуальному варианту. Ввод элементов матрицы осуществлять с клавиатуры. Во время отладки и тестирования программы размер матрицы можно уменьшить. При выводе матрицы следить за тем, чтобы ее столбцы были выровнены. На экран вывести исходные данные и результат. Использовать форматный вывод.

Варианты заданий

Вариант 1

1. Сформировать целочисленную матрицу А размером 7×8, состоящую из 0 и 1 по следующему правилу: если сумма индексов элемента четная, элемент будет нулевым, если нечетная – единичным.

2. Дана вещественная матрица X размера 6×8. В каждом столбце найти наибольшее значение и сформировать одномерный массив из найденных значений.

Вариант 2

1. В заданной целочисленной квадратной матрице Y порядка n (n < = 8) определить номера строк, все элементы которых четны.

2. Даны вещественная матрица Z размером 8×10 и число X. Поменять местами минимальный элемент матрицы и элемент, значение которого равно заданному X. Если указанный элемент в матрице отсутствует, вывести сообщение об этом.

Вариант 3

1. Дана целочисленная квадратная матрица Y порядка n (n <=8). Вычислить среднее арифметическое отрицательных элементов, расположенных на главной и побочной диагоналях.

2. Дана вещественная матрица Z размером 10×12. В каждом ее столбце найти наибольшее и наименьшее значения и сформировать вектор, состоящий из сумм наибольшего и наименьшего элементов каждого столбца.

Вариант 4

1. Дана вещественная матрица С размером 6×6, все элементы которой различны. Найти скалярное произведение строки с наибольшим элементом и столбца с наименьшим элементом, т.е. вычислить , где i max – номер строки с наибольшим элементом, j min – номер столбца с минимальным элементом.

2. Дана целочисленная матрица R размером 7×8. В каждом
ее столбце определить количество четных положительных зна-чений и сформировать из найденных количеств одномерный
массив D.

Вариант 5

1. Дана целочисленная матрица X размером 10×10. Среди элементов, расположенных выше главной диагонали, найти наибольшее значение.

2. Дана вещественная матрица А размером 6×8. Добавить к ней столбец, состоящий из средних арифметических положительных значений строк матрицы.

Вариант 6

1. Дана целочисленная матрица X размером 10×12. Сформировать вектор, каждый элемент которого равен первому четному элементу соответствующего столбца; если четных элементов в столбце нет, присвоить 0.

2. В заданной вещественной матрице B размером 7×8 удалить строку, содержащую наибольшее количество положительных значений.

Вариант 7

1. Дана вещественная матрицы А размером 6×8. Сформировать одномерный массив В, состоящий из отрицательных значений матрицы в порядке следования по столбцам.

2. Для целочисленной матрицы А размером 10×10 определить среднее арифметическое значение элементов, лежащих ниже главной диагонали.

Вариант 8

1. Дана вещественная матрица М размером 7×8. Преобразовать матрицу, поэлементно вычитая последнюю строку из всех строк, кроме последней.

2. Дана целочисленная матрица В размером 6×6. Вывести номера столбцов, элементы которых образуют возрастающую последовательность.

Вариант 9

1. В заданной целочисленной матрице A размером m × n (m, n<= 8) определить количество строк, состоящих только из нулей.

2. Дана матрица В размером 7×7. Преобразовать ее так,
чтобы минимальные элементы строк оказались на главной диаго-
нали.

Вариант 10

1. Дана квадратная матрица А размером n × n (n<= 6 ). Определить, является ли она симметричной относительно главной диагонали.

2. Дана вещественная матрица C размером 7×8. В каждой строке определить количество элементов, бóльших среднего арифметического этой строки.

Вариант 11

1. Дана вещественная матрица D размером 7×9. Упорядочить ее строки по возрастанию, используя метод попарно-обменной сортировки.

2. Сформировать одномерный массив, каждый элемент которого равен количеству отрицательных элементов соответствующего столбца заданной целочисленной матрицы А размером 5×8.

Вариант 12

1. Дана вещественная матрица D размером 7×9. Упорядочить ее столбцы по убыванию, используя метод выбора (поиском максимума).

2. Определить, сколько строк в заданной целочисленной квадратной матрице А порядка n (n<= 6) содержат хотя бы один нуль.

Вариант 13

1. Дана целочисленная матрица В размером 5×8. Полу-
чить массив С из 0 и 1, в котором с_i= 1, если в i -й строке матрицы есть хотя бы один отрицательный элемент, и с_i= 0 в противном
случае.

2. В каждом столбце заданной матрицы D размером 9×10 найти позицию максимального значения и сформировать из них одномерный массив.

Вариант 14

1. Дана целочисленная матрица С размером 6×6. Определить количество и сумму элементов, бóльших среднего арифметического элементов матрицы.

2. Дана вещественная матрица D размером 7×9. Преобразовать матрицу, заменив нулем последний отрицательный элемент каждого столбца.

Вариант 15

1. В каждой строке заданной вещественной матрицы В размером 9×8 поменять знак у максимального по модулю элемента на противоположный.

2. В каждом столбце матрицы В размером 6×8 найти номер элемента, наиболее близкого к среднему значению этого столбца.

Вариант 16

1. В каждой строке матрицы А размером 7×9 поменять местами первый элемент и максимальный по модулю.

2. Дана вещественная матрица D размером 10×12. Выяснить, имеются ли в матрице нулевые элементы. Если имеются, то вывести их индексы; если нет, то вывести сообщение об этом.

Вариант 17

1. Дана вещественная квадратная матрица D порядка n (n < = 10). В строках с отрицательным элементом на главной диагонали найти сумму элементов.

2. В заданной целочисленной матрице А размером 6×9 поменять местами столбец с наибольшим элементом со столбцом с наименьшим элементом (элементы не повторяются).

Вариант 18

1. Дана вещественная матрица C размером 7×8. Удалить
из нее строку с наибольшим количеством положительных эле-
ментов.

2. В каждой строке матрицы В размером 6 × 6 найти сумму элементов, больших заданного значения Z.

Вариант 19

1. Дана матрица Х размером 5×7 и массив Y из 7 элементов. Поэлементно вычесть массив Y из каждой строки матрицы.

2. Вычислить среднее арифметическое значение максимального и минимального элементов матрицы А размером 9×9, лежащих на побочной диагонали.

Вариант 20

1. Дана матрица А размером 4×6. Вывести номера строк, состоящих только из положительных значений, если таких нет, вывести сообщение об этом.

2. Дана вещественная матрица C размером 5×5. Поменять местами максимальный и минимальный элементы побочной диагонали.

Вариант 21

1. Дана матрица А размером n×m (n<= 7, m<= 8) и массив С из n элементов. Заменить столбец матрицы с наименьшей суммой модулей элементов массивом С.

2. Даны натуральное число n, вещественное число X и мат-рица Y размером n × n (n <=10). Получить вектор B, каждый эле-мент которого состоит из 1 и 0. Элемент b_i= 1, если все элементы
i -й строки матрицы не превосходят X, и b_i= 0 в противном слу-
чае.

Вариант 22

1. Определить седловые точки матрицы М размером 7×8. Седловая точка – элемент, являющийся одновременно максимальным в своей строке и минимальным в своем столбце.

2. Дана целочисленная матрица Y размером n × n (n <=8). Проверить, является ли заданная матрица латинским квадратом (каждая строка и каждый столбец содержат все числа от 1 до n).

Контрольные вопросы

1. Что представляет собой матрица?

2. Как объявить двумерный массив?

3. Как располагается матрица в памяти компьютера?

4. Как ввести элементы двумерного массива с клавиатуры?.

5. Как заполнить элементы матрицы случайными числами?

6. Как правильно вывести матрицу?

7. Как обратиться к элементу матрицы?

8. Каковы особенности обработки матрицы?

9. Чем отличается просмотр элементов матрицы по столбцам от просмотра по строкам?

10. Можно ли просмотреть все элементы матрицы в одном цикле?

Лабораторная работа № 6

Подпрограммы

Цель работы – научиться использовать функции и процедуры для выполнения однотипных действий над различными данными, изучить структуру подпрограмм, получить навыки описания процедур и функций, научиться описывать формальные параметры подпрограмм разного вида и правильно задавать фактические параметры.

Постановка задачи

Написать две программы согласно индивидуальному варианту. Одно задание должно быть выполнено с использованием функции, другое – с использованием процедуры. Ввод и вывод массивов и других данных не объединять с обработкой данных.
На экран вывести исходные данные и результат. Использовать форматный вывод.

Варианты заданий

Вариант 1

1. Даны три матрицы: Х, Y, Z размером n × m (n, m<= 12). Определить, в какой из них среднее арифметическое положительных элементов больше.

2. Даны две квадратные матрицы: А размером 6×6 и В размером 10×10. Сформировать одномерные массивы А1 и В1 из элементов главных диагоналей матриц А и В.

Вариант 2

1. Для 10 значений Х, изменяющегося от - А до А (А задано) с постоянным шагом, вычислить с точностью eps значение суммы . Результат вычисления каждой суммы записать в массив.

2. Для заданной матрицы А сформировать одномерный масс
сив B, содержащий суммы максимальных и минимальных элементов соответствующих столбцов матрицы.

Вариант 3

1. В массивах Х и Y найти минимумы (количество минимумов в каждом массиве может быть больше одного), то есть сформировать новые массивы из позиций минимальных значений в массивах Х и Y. Поменять местами значения минимумов в массивах.

2. Даны две матрицы А и В размером n × m (n, m <= 15). Вывести ту из них, в которой среднее арифметическое отрицательных элементов меньше. Для определения среднего значения в одной матрице использовать функцию.

Вариант 4

1. Для каждого из массивов Х и Y получить массивы из позиций элементов, равных заданному числу Z.

2. Для заданной матрицы найти номер столбца с минимальной суммой положительных элементов. Использовать подпрограмму для нахождения суммы в одном столбце.

Вариант 5

1. Дана вещественная матрица D размером 8×12. Сформировать одномерный массив, состоящий из номеров столбцов, элементы которых образуют возрастающую последовательность. Для проверки одного столбца использовать функцию.

2. Для каждого из массивов: А из 10 элементов, В из 20 и С из 12 – произвести перестановку элементов, поменяв порядок их следования на обратный.

Вариант 6

1. Найти меньшие корни квадратных уравнений: x ² – 2 x – a = 0 и ax ² – bx – 2 = 0 (считать, что все корни действительные).

2. В заданной вещественной матрице В размером 7×8 обнулить столбцы, в которых имеются нулевые элементы (все элементы таких столбцов сделать нулевыми).

Вариант 7

1. Для каждого из элементов целочисленного массива С выяснить, является ли он факториалом какого-либо числа, и если да, то какого. Использовать функцию для проверки одного числа, результатом которой является n, если , и 0 в противном случае.

2. Bычислить , где и – сумма и количество отрицательных четных элементов целочисленного массива X из n элементов (n<= 30), а и – сумма и количество отрицательных четных элементов целочисленного массива Y из m элементов (m <=20).

Вариант 8

1. Даны два одномерных массива: А из 10 элементов и В из 15 элементов. Сформировать два новых массива: Х из элементов массива А, не входящих в массив В, и Y из элементов массива В, не входящих в массив А.

2. Даны три одномерных массива A, B и C (три вектора) с одинаковым количеством элементов. Получить S= (b, c) – (a, a), где (x, y) – скалярное произведение векторов x и y, _.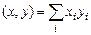

Вариант 9

1. Дана матрица D размером n × m (n, m <= 20). Сформировать три одномерных массива: А – из элементов матрицы D, лежащих в диапазоне от -5 до 5, в порядке следования по строкам, В – из элементов от 10 до 20, С – от 30 до 50. Использовать подпрограмму для выборки в новый массив элементов для одного диапазона.

2. Дан массив X из n (п ≤ 10) элементов. Сформировать массив Y, в котором y_i =1/(x_i +1) +2/(x_i +2)+3/(x_i +3)+... + 12/(x_i +12). Использовать подпрограмму для вычисления одного y_i .

Вариант 10

1. Дана матрица А размером n × m (n, m <=15). В каждой нечетной ее строке найти среднее арифметическое элементов, не принадлежащих отрезку от 0 до 10, и сформировать из них одномерный массив. Для расчёта значения в одной строке использовать подпрограмму.

2. Дана последовательность { a_i }. Для каждого элемента последовательности определить количество элементов левее a_i, которые по модулю меньше a_i, и количество элементов справа от a_i, которые по модулю больше a_i. Использовать подпрограмму, производящую вычисления для одного элемента a_i.

Вариант 11

1. Дан одномерный массив A размером n (n <=30). Получить новый массив B, каждый элемент которого вычисляется по формуле .

2. Дана квадратная матрица B размером 10×10. Преобразовать её к такому виду, чтобы на побочной диагонали стояли максимальные элементы всех строк. Использовать процедуру для поиска максимального элемента строки и перестановки его с элементом главной диагонали в этой строке.

Вариант 12

1. Дана матрица А размером 10×10. В каждом ее столбце обнулить минимальное количество элементов так, чтобы сумма элементов столбца не превышала заданного Р. Использовать подпрограммы для преобразования одного столбца и поиска максимума в столбце.

2. Даны два массива: Х из n элементов и Y из m (n, m <=15). Найти количество элементов массива Х, не лежащих в диапазоне от 0 до 10, и количество элементов массива Y, не лежащих в диапазоне от 1 до 5. Для нахождения количества элементов, не лежащих в диапазоне от А до В, использовать функцию.

Вариант 13

1. Заданный массив целых чисел А делится на три части двумя элементами: максимальным и минимальным. Определить сумму и количество четных значений в каждой части массива. Использовать подпрограммы для нахождения индексов минимального и максимального элементов и подсчёта суммы и количества четных значений в одной части массива.

2. Дана квадратная матрица А размером 6×6. Определить номера строк, не содержащих отрицательных элементов. Для проверки одной строки использовать функцию.

Вариант 14

1. Даны матрица Х размером n × m (n <=10, m – нечетное число <10) и одномерный массив Y из n элементов. Заменить массивом Y первый, средний и последний столбцы матрицы. Для замены одного столбца использовать подпрограмму.

2. Дана матрица С размером 7×3. Найти номер строки с максимальной суммой элементов. Использовать функцию для нахождения суммы в одной строке.

Вариант 15

1. Дан целочисленный массив А из 3 n элементов (n <=10). В каждой десятке найти наименьшее значение и вывести ту часть массива, где минимум больше. Для ввода, вывода массива и поиска минимума в одной части массива использовать подпрограммы.

2. Дана вещественная матрица В размером 5×7. Заменить единицами те столбцы матрицы, где положительных значений больше, чем отрицательных. Использовать подпрограммы для ввода, замены столбцов и вывода матрицы.

Вариант 16

1. Дана матрица А размером n × m (n, m <=16) и два числа c и d. В каждом четном столбце матрицы найти среднее арифметическое элементов, не принадлежащих отрезку [ c, d ], и сформировать из них одномерный массив. Для нахождения среднего значения в одном столбце использовать функцию.

2. В заданной вещественной матрице В размером 7×8 заменить на нули те строки, в которых есть хотя бы один нулевой элемент (все элементы таких строк сделать нулевыми).

Вариант 17

1. Дана вещественная матрица D размером 8×12. Проверить, что суммы элементов в столбцах матрицы образуют возрастающую последовательность. Для определения суммы элементов в одном столбце использовать функцию.

2. Для каждого из массивов А, B, C из 2 n элементов (n <=20) произвести перестановку элементов по следующему правилу: a_{n +1}, a_{n +2},…, a _{2 n} , a ₁, a ₂,…, a_n.

Вариант 18

1. Для заданной матрицы А размером n × n (n <=20) найти максимум из всех минимальных элементов матрицы по столбцам. Для нахождения минимального элемента одного столбца использовать подпрограмму.

2. Написать процедуру, преобразующую одномерный массив A1 из n ² элементов в квадратную матрицу A2 размером n × n. Использовать её для массива X из 36 элементов.

Вариант 19

1. Дана квадратная матрица А размером 10×10. Преобразовать её к такому виду, чтобы на главной диагонали стояли минимальные элементы всех столбцов. Использовать процедуру для поиска минимального элемента столбца и перестановки его с диагональным элементом в этом столбце.

2. Дан массив Х из п элементов (n <=20). Значения элементов принадлежат интервалу [-10, 10]. Этот интервал разбивается на m одинаковых подынтервалов (m вводится). Используя функцию, определить количество элементов массива Х, попадающих в каждый подынтервал.

Вариант 20

1. Для каждого значения z (z =1; 1.2; 1.4;...;2.6) вычислить значение полинома p (z)= a ₆ z ⁶ + a ₅ z ⁵ + a ₄ z ⁴ +...+ a ₁ z + a _0. Использовать подпрограмму для нахождения значения полинома для одного z_i.

2. Дана целочисленная матрица А размером 10×12. Сформировать вектор D, состоящий из номеров строк, содержащих хотя бы один отрицательный элемент. Использовать процедуру для формирования вектора.

Вариант 21

1. Дана матрица А размером n × m (n, m <=15). Отсортировать в порядке убывания четные строки матрицы. Использовать подпрограмму для сортировки одной строки.

2. Координаты точек на плоскости заданы матрицей А размером 20×2. В первом столбце записаны координаты Х, во втором – координаты Y. Найти количество точек, попадающих внутрь окружности с радиусом r_i и центром в начале координат. Значения r_i заданы массивом R из 10 элементов.

Вариант22

1. В заданной матрице С размером n × m (n, m<= 20) найти количество столбцов, которые образуют арифметическую прогрессию. Использовать подпрограмму проверки одного столбца.

2. Элементы матрицы A размером n × n (n<= 10) вычисляются по формуле А_ij = (-1) ⁱ × i× j. Получить матрицу В, в которой элементы определяются по правилу: . Использовать подпрограммы для формирования матриц А и В, нахождения максимума в одной строке матрицы А, вывода матриц.

Контрольные вопросы

1. Для чего используются подпрограммы?

2. Перечислите виды подпрограмм и дайте им характеристики.

3. Где располагаются описания подпрограмм?

4. Назовите отличия функций и процедур.

5. Какие переменные называются глобальными?

6. Что такое формальные параметры и как они используются?

7. Что такое локальные переменные?

8. Чем отличаются формальные параметры от локальных переменных?

9. Какие виды формальных параметров существуют в Паскале? Дайте им характеристику.

10. Что такое фактические параметры и как они используются?

11. Чем может являться фактический параметр, если соответствующий ему формальный параметр описан как параметр-пере-менная?

Не нашли, что искали? Воспользуйтесь поиском: