
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Методика определения коэффициента трения качения
Наклонный маятник представляет собой шарик радиусом R, который качается по наклонной плоскости, удерживаемый легкой нерастяжимой нитью длины l, закрепленной в точке О (рис. 4). Плоскость образует с вертикалью угол β.

В результате действия сил трения, полная механическая энергия E колебаний маятника уменьшится на некоторую величину ΔE за n полных колебаний. Поскольку силы трения являются неконсервативными, то ΔE должно быть равно работе сил трения ΔE = A. Убыль полной механической энергии маятника равна разности потенциальных энергий в начальном крайнем положении WП 0 и в его крайнем положении через n колебаний WПn:
 , (1)
, (1)
где Δh – изменение высоты подъема маятника при амплитудных отклонениях через n колебаний.
Маятник, совершая колебания, движется по дуге окружности АВМС. При этом выполняется работа против сил трения качения, на что расходуется запасенная в начальном положении А потенциальная энергия
 ,
,
где h = | QP | (рис. 4).
Так как | QP | = | QМ | cosβ, а  , то
, то 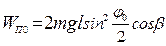 .
.
При малом угле отклонения  (2)
(2)
Следовательно  . (3)
. (3)
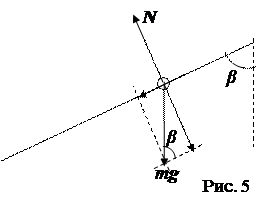
Сила трения качения  , где N – модуль силы нормальной реакции опоры (наклонной плоскости). Как видно из рисунка 5, нормальная реакция N компенсирует составляющую силы тяжести, перпендикулярную к наклонной плоскости. Следовательно,
, где N – модуль силы нормальной реакции опоры (наклонной плоскости). Как видно из рисунка 5, нормальная реакция N компенсирует составляющую силы тяжести, перпендикулярную к наклонной плоскости. Следовательно,  и
и 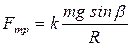 .
.
Сила трения все время направлена против движения, поэтому работа против этой силы  , где s – вся длина пути, проходимого шариком при его колебательном движении по дуге АВМС.
, где s – вся длина пути, проходимого шариком при его колебательном движении по дуге АВМС.
Например, за полное первое колебание шарик смещается последовательно из точки А в точку М, пройдя путь  , далее в точку С (амплитудное отклонение вправо, длина пути
, далее в точку С (амплитудное отклонение вправо, длина пути 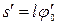 ), назад в точку М (путь тот же
), назад в точку М (путь тот же 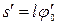 ) и из М влево до амплитудного отклонения (
) и из М влево до амплитудного отклонения ( ). Так как по мере движения расходуется энергия, то
). Так как по мере движения расходуется энергия, то  .
.
Поскольку сила трения качения мала, то до остановки маятник совершает достаточно большое число колебаний, поэтому изменение амплитудного угла отклонения за одно первое колебание  значительно меньше начального угла отклонения φ0: Δφ01<<φ0. Поэтому амплитудное отклонение вправо с большой точностью можно считать как среднее арифметическое между φ0 и φ1:
значительно меньше начального угла отклонения φ0: Δφ01<<φ0. Поэтому амплитудное отклонение вправо с большой точностью можно считать как среднее арифметическое между φ0 и φ1:
 .
.
Путь, проходимый за одно полное первое колебание:  и совершаемая на нем работа против сил трения
и совершаемая на нем работа против сил трения
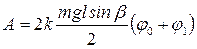 . (4)
. (4)
Эта работа совершается за счет уменьшения потенциальной энергии
 . (5)
. (5)
Приравнивая (4) и,(5), получим
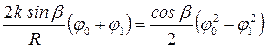 ; и с учетом
; и с учетом  найдем
найдем  . (6)
. (6)
Как видим из (6), изменение угла за одно полное колебание не зависит от величины начального угла отклонения, если выполнено условие (2). Следовательно, за каждое полное колебание угол амплитудного отклонения будет уменьшаться на одну и ту же величину, определяемую выражением (6). После п колебаний амплитуда уменьшится на величину
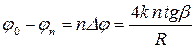 ,
,
где φn – угол амплитудного отклонения наклонного маятника после n полных колебаний.
Из последнего выражения получаем рабочую формулу для определения коэффициента трения качения
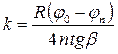 . (7)
. (7)
В формуле (7) углы должны быть выражены в радианах. Так как шкала в лабораторной установке проградуирована в градусах, то при использовании этой угловой меры правую часть (7) необходимо умножить на число, равное количеству радиан в одном градусе (1°= 0,0175 рад), и учесть в искомом коэффициенте число 4 в знаменателе (7) (0,0175/4 = 4,38·10-3).
 . (8)
. (8)
Задание
1. Измерить коэффициент трения качения для шариков и пластин
из разных материалов (по заданию преподавателя).
2. Рассчитать относительную и абсолютную ошибки измерений
коэффициента трения.
Контрольные вопросы
1. Что такое внешнее и внутреннее трение?
2. Какими факторами определяется коэффициент трения скольжения и коэффициент трения качения?
3. Размерности коэффициента трения скольжения и качения.
4. Какие физические законы используются при выводе рабочей формулы?
5. Объясните смысл всех величин, входящих в рабочую формулу.
Литература
1. Савельев И.В. Курс общей физики. Т.1. М.: Наука, 1977, с.64-67.
2. Трофимова Т.И. Курс физики. М.: Высшая школа, 1985, с.15-17.
3. Петровский И.И. Механика. М.: Изд-во БГУ, 1973, с.131-142
Лабораторная работа № 9
Не нашли, что искали? Воспользуйтесь поиском: