Лекция Основы алгоритмизации

Слово «алгоритм» происходит от algorithmi – латинской формы написания имени великого математика Моххамеда бен Аль-Хорезми, который в своей книге «Об индийском счете» сформулировал правила записи натуральных чисел с помощью арабских цифр и правила действий над ними столбиком. Первоначально под алгоритмами и понимали только правила выполнения четырех арифметических действий над многозначными числами. В дальнейшем это понятие стали использовать для обозначения любой последовательности действий, приводящих к решению поставленной задачи.

В настоящее время не существует единого определения данного термина. В качестве наиболее распространенных можно привести следующие:

1. Алгоритм - это конечный набор правил, который определяет последовательность операций для решения конкретного множества задач и обладает пятью важными чертами: конечность, определённость, ввод, вывод, эффективность (Д. Э. Кнут);

2. Алгоритм - это всякая система вычислений, выполняемых по строго определённым правилам, которая после какого-либо числа шагов заведомо приводит к решению поставленной задачи (А. Колмогоров);

3. Алгоритм - это точное предписание, определяющее вычислительный процесс, идущий от варьируемых исходных данных к искомому результату (А. Марков);

4. Алгоритм - строго детерминированная последовательность действий, описывающая процесс преобразования объекта из начального состояния в конечное, записанная с помощью понятных исполнителю команд;

5. Алгоритм - это последовательность действий, направленных на получение определённого результата за конечное число шагов;

6. Алгоритм - это понятные и точные предписания исполнителю совершить конечное число шагов, направленных на решение поставленной задачи;

7. Алгоритм - это некоторый конечный набор рассчитанных на определённого исполнителя операций в результате выполнения которых через определённое число шагов может быть достигнута поставленная цель или решена задача определённого типа;

Алгоритм всегда создается в расчете на некоторого исполнителя. Исполнитель алгоритма - это некоторая абстрактная или реальная (техническая, биологическая или биотехническая) система, способная выполнить действия, предписываемые алгоритмом. Примером исполнителя может являться человек, робот, станок с автоматическим управлением, бытовая техника и т.д. В информатике универсальным исполнителем алгоритмов является компьютер.

Исполнители делятся на два класса: формальные и неформальные. Если выполняя алгоритм, исполнитель может не вникать в смысл того, что он делает и тем не менее получать нужный результат, то в таком случае говорят, что исполнитель действует формально, т.е. отвлекается от содержания поставленной задачи и только выполняет строгой последовательности все действия. Это и есть формальный исполнитель. В отличие от формального, неформальный исполнитель всегда интересуется, зачем он выполняет то или иное действие, стремится выполнить его лучше, эффективнее (с его точки зрения).

Основными характеристиками исполнителя являются: среда, система команд, элементарные действия, отказы.

Среда – это условия, в которых исполнитель может выполнять команды. Исходные данные и результаты любого алгоритма всегда принадлежат среде того исполнителя, для которого предназначен алгоритм.

Свойством, характеризующим исполнителя, является то, что он может выполнять команды. Совокупность всех команд, которые исполнитель может выполнить, называется системой команд исполнителя (СКИ). Для каждой команды должны быть заданы условия применимости (в каких состояниях среды может быть выполнена команда) и описаны результаты выполнения команды. За каждой командой из системы команд исполнителя закреплено конкретное элементарное действие. После вызова команды исполнитель совершает элементарное действие, соответствующее данной команде.

Отказы исполнителя возникают при вызове команды в недопустимом для данной команды состоянии среды. Существует два вида отказов:

1. Отказ «НЕ МОГУ» - возникает в том случае, если исполнитель по каким-либо причинам не в состоянии выполнить команду;

2. Отказ «НЕ ПОНИМАЮ» - возникает в том случае, если исполнителю задана команда, не входящая в его СКИ;

Неформальные исполнители обладают еще одним видом отказов – отказом «НЕ ХОЧУ».

Значение слова «алгоритм» схоже со значениями слов «метод», «процесс». Однако в отличие от метода или процесса алгоритм характеризуется следующими свойствами:

1. Дискpетность (прерывность, раздельность) - алгоpитм должен состоять из последовательных пpостых (или pанее опpеделенных) шагов (этапов);

2. Массовость - применимость алгоритма ко всем задачам рассматриваемого типа при любых исходных данных. Исходные данные могут выбиpаться из некотоpой области, котоpая называется областью пpименимости алгоpитма;

3. Детерминированность (определенность, точность) - каждый шаг алгоритма должен быть строго определен и не должен допускать произвольных толкований. Также строго определен должен быть и порядок выполнения отдельных шагов;

4. Pезультативность (конечность) состоит в том, что за конечное число шагов алгоpитм либо должен пpиводить к pешению задачи, либо останавливаться из-за невозможности получить решение с выдачей соответствующего сообщения;

5. Понятность для исполнителя - исполнитель алгоритма должен понимать, как его выполнять. Иными словами, имея алгоритм и произвольный вариант исходных данных, исполнитель должен знать, как надо действовать для выполнения этого алгоритма;

Существуют следующие формы представления алгоритмов:

1. словесная (запись на естественном языке);

2. псевдокод;

3. графическая (блок-схема);

4. на языке программирования;

Словесный способ представляет собой структуру алгоритма на естественном языке (например, на русском). Никаких правил составления словесного описания не существует. Примером словесной записи может являться инструкция к какому-либо прибору. Словесный способ не имеет широкого распространения, так как такие описания строго не формализуемы, страдают многословностью записей, допускают неоднозначность толкования отдельных предписаний.

В качестве примера словесного описания приведем алгоритм нахождения максимального из двух чисел.

1. Получим два значения чисел X и Y;

2. Сравним X и Y;

3. Если X меньше Y, значит большее число Y. Запомним его в M;

4. В противном случае большее число X. Запомним его в M;

5. Выдадим значение M;

Псевдокод занимает промежуточное место между естественным и формальным языками. С одной стороны, он близок к обычному естественному языку, поэтому алгоритмы могут на нем записываться и читаться как обычный текст. С другой стороны, в псевдокоде используются некоторые формальные конструкции и математическая символика, что приближает запись алгоритма к общепринятой математической записи. Описание алгоритма на псевдокоде позволяет выявить основные этапы решения задачи перед ее точной записью на языке программирования.

В псевдокоде не приняты строгие синтаксические правила для записи команд, присущие формальным языкам, что облегчает запись алгоритма на стадии его проектирования и дает возможность использовать более широкий набор команд, рассчитанный на абстрактного исполнителя. Единого или формального определения псевдокода не существует, поэтому возможны различные псевдокоды, отличающиеся набором служебных слов и базовых конструкций.

Блок-схема это описание алгоритма с помощью геометрических фигур с линиями-связями, показывающими порядок выполнения отдельных инструкций. Этот способ имеет ряд преимуществ, главным из которых является наглядность.

В блок-схеме каждой формальной конструкции соответствует определенная геометрическая фигура или связанная линиями совокупность фигур.

Фигура	Описание
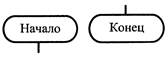
	Начало/конец алгоритма
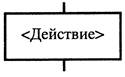
	Процесс, описывающий отдельное действие
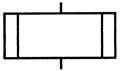
	Предопределенный процесс, предназначенный для обращения ко вспомогательным алгоритмам
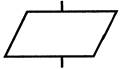
	Ввод-вывод с неопределенного носителя
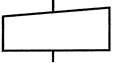
	Ввод с клавиатуры
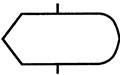
	Вывод на монитор
	Вывод на печатающее устройство
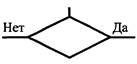
	Решение (проверка условия)
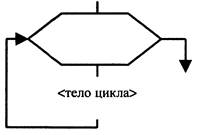
	Цикл с параметром
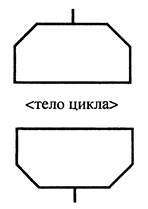
	Граница цикла. Описывает циклы, управляемые условиями
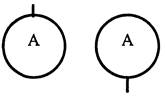
	Соединительные блоки

Описания алгоритмов в трех рассмотренных формах допускают некоторый произвол при изображении команд. Хотя это описание достаточно для того, чтобы человек понял и исполнил алгоритм, на практике исполнителем алгоритмов в основном выступают компьютеры. Поэтому алгоритм, предназначенный для исполнения на компьютере, должен быть записан на понятном ему языке. Такой формализованный язык называют языком программирования. Таким образом, язык программирования - формальная знаковая система, предназначенная для записи компьютерных программ. Язык программирования определяет набор лексических, синтаксических и семантических правил, задающих внешний вид программы и действия, которые выполнит исполнитель (компьютер) под ее управлением. Компьютерная программа - последовательность инструкций, предназначенная для исполнения устройством управления вычислительной машины. Процесс создания компьютерных программ носит название программирование, а людей, занимающихся этим видом деятельности, называют программистами.

Особую роль в информатике играют вычислительные алгоритмы, в которых используются величины. Каждая величина имеет имя, значение и тип. Имя величины служит для обращения к ней в алгоритме. Именование величин подчиняется следующим правилам:

1. Имя величины может содержать буквы латинского алфавита, цифры и некоторые специальные символы;

2. Имя величины должно обязательно начинаться с буквы или с символа подчеркивания;

3. В именах величин не должно быть пробелов;

Тип величины определяет:

1. Какие значения может принимать величина в процессе выполнения алгоритма;

2. В каких выражениях и как эту величину можно использовать;

Если значением величины может быть только целое число, такая величина называется целой или целочисленной, если любое вещественное число – то вещественной. Бывают также логические, строковые и другие типы величин.

Величины разделяются на переменные и константы. Переменная – это величина, которая по ходу выполнения алгоритма может многократно менять свое значение. Константа – это величина, которая во время выполнения алгоритма свое значение не меняет.

В ходе выполнения алгоритма над переменными можно выполнять различные действия. Эти действия выполняются при помощи операторов. Существуют различные категории операторов (например, математические, логические и т.д.). К математическим операторам относятся:

* - умножение

/ - деление

+ - сложение

- - вычитание

div (\) – целочисленное деление

mod - деление по модулю (остаток от деления);

Объекты, над которыми выполняются действия, называются операндами. Операторы и операнды формируют выражения.

Во время выполнения алгоритма в каждый конкретный момент времени переменная имеет какое-то значение или не определена. Для того чтобы изменить значение переменной используется операция присваивания, обозначаемая знаком :=. В общем виде операция присваивания выглядит так:

<имя_переменной>:=выражение;

При выполнении данной операции сначала вычисляется значение выражения, а затем его результат присваивается переменной с указанным именем и записывается в память.

Элементарные шаги, входящие в алгоритм, можно объединять в алгоритмические конструкции. В зависимости от того, какая конструкция используется, выделяют три вида алгоритмов:

1. Линейный (следование);

2. Разветвляющийся (ветвление);

3. Циклический;

Линейный алгоритм – это алгоритм, все этапы которого выполняются однократно и строго последовательно сверху вниз.

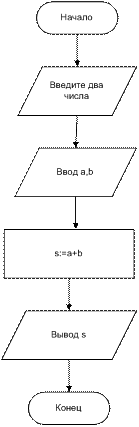
Пример 1. Составить блок-схему алгоритма вычисления суммы двух чисел

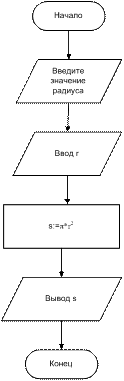
Пример 2. Составить блок-схему алгоритма вычисления площади круга

Разветвляющийся алгоритм - это алгоритм, в котором в зависимости от условия выполняется либо одна, либо другая последовательность действий.

Различают неполное (если – то) и полное (если – то - иначе) ветвление. Неполным называется ветвление, в котором действия выполняются только на одной ветви.

Полным называется ветвление, в котором действия выполняются на обеих ветках.

Оба типа ветвления работают одинаково: сначала вычисляется элемент <условие>. Результат проверки условия всегда есть логическая величина. Если результат имеет значение «Истина», то выполняются операторы первой ветки, а если «Ложь», то второй. Затем управление переходит к точке слияния.

Пример 1. Составить блок-схему алгоритма нахождения абсолютного значения числа, вводимого с клавиатуры

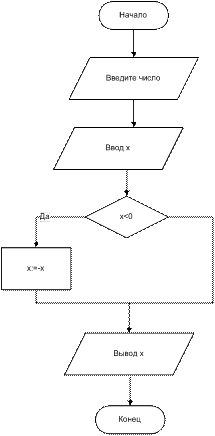
Пример 2. Составить блок-схему алгоритма нахождения максимального из двух введенных чисел

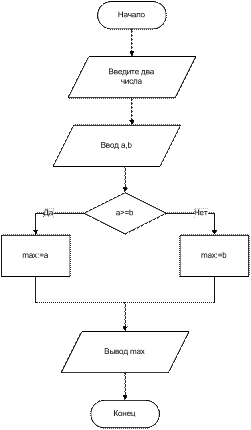
В блоке проверки условия можно одновременно проверять несколько условий, объединяя их логическими операторами. В качестве таких операторов можно использовать AND (Логическое «И») и OR (Логическое «ИЛИ»). В этом случае образуются составные условия. Простые условия, входящие в состав составного, для удобочитаемости рекомендуется заключать в скобки.

Пример 1. Составить блок-схему алгоритма определения принадлежности точки X промежутку [a;b]

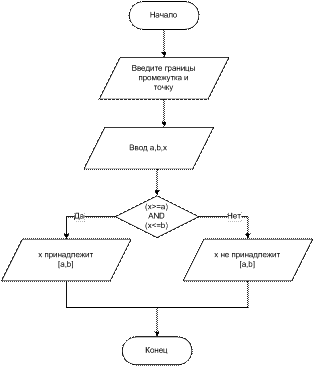
Пример 2. Составить блок-схему алгоритма определения того, заканчивается ли введенное число на одну из двух введенных цифр.

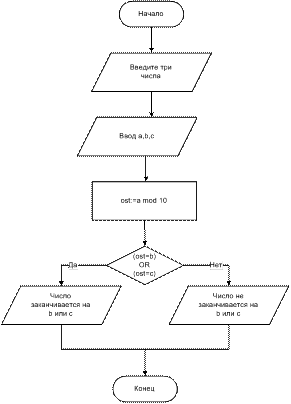
Блоки проверки условий можно вкладывать друг в друга без ограничений. В результате можно проверять сложные условия.

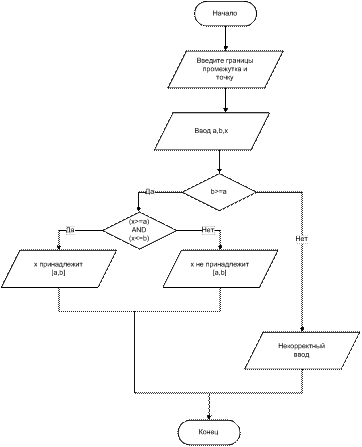
Пример. Модифицировать блок-схему алгоритма проверки принадлежности точки промежутку так, чтобы перед определением принадлежности проверялась корректность введенных данных

Циклический алгоритм – это алгоритм, в котором некоторая последовательность действий выполняется либо определенное количество раз, либо пока истинно некоторое условие. Повторяющаяся последовательность действий называется телом цикла.

Существует три вида циклов:

1. Цикл со счетчиком (с параметром);

2. Цикл с предусловием (цикл «ПОКА»);

3. Цикл с постусловием (Цикл «ДО»);

Цикл со счетчиком используется в тех случаях, когда количество повторений цикла известно заранее. Цикл управляется специальной переменной, которая называется счетчиком или параметром цикла. Для параметра указывается его начальное значение, конечное значение и шаг изменения. После каждого прохода значение параметра автоматически изменяется на указанный шаг.

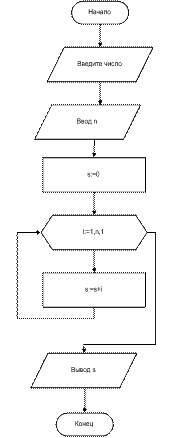
Пример 1. Составить блок-схему алгоритма вычисления суммы чисел от 1 до n

Пример 2. С клавиатуры вводится десять чисел. Составить блок-схему алгоритма, подсчитывающего их среднее арифметическое

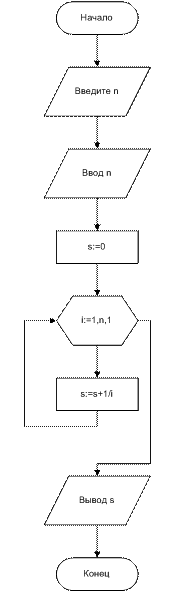
Пример 3. Составить блок-схему алгоритма вычисления суммы последовательности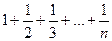

Если количество повторений в цикле заранее неизвестно, то используются циклы, управляемые условиями. Как уже было сказано, эти циклы разделяются на циклы с предусловием и циклы с постусловием.

Цикл с предусловием работает следующим образом: вначале проверяется условное выражение. Если оно истинно, выполняется тело цикла. Затем снова происходит вычисление условного выражения. Так происходит до тех пор, пока результат проверки условия не даст ложный результат. После этого происходит выход за пределы цикла.

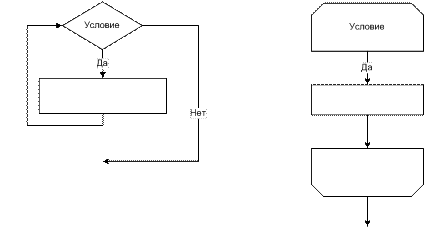
Особенностью данного цикла является то, что если первая же проверка условного выражения даст ложный результат, тело цикла не будет выполнено ни разу.

Пример. Составить блок-схему алгоритма вычисления суммы положительной последовательности вводимых с клавиатуры чисел, оканчивающейся нулем

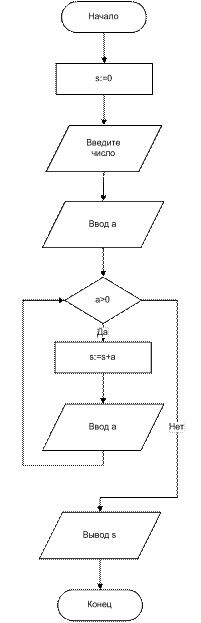
Цикл с постусловием работает следующим образом: вначале выполняется тело цикла, затем проверяется условное выражение. Если оно ложно, вновь выполняется тело цикла. Цикл выполнятся до тех пор, пока условие не станет истинным. В отличие от цикла с постусловием, тело цикла с предусловием всегда будет выполнено хотя бы один раз.

Во многих языках программирования данный цикл наоборот выполняется до тех пор, пока условие истинно. Как только условие станет ложным, происходит выход из цикла.

Пример. Переделать предыдущую схему с использованием цикла с постусловием

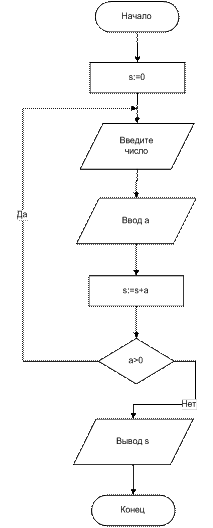
Одной из распространенных ошибок, связанных с циклами, управляемыми условиями, является неверное указание условия завершения цикла. В таких случаях цикл будет выполняться бесконечное количество раз. Эта ситуация называется зацикливанием. К зацикливанию может также привести такая логическая ошибка, как отсутствие изменения в теле цикла переменной, которая проверяется в условном выражении

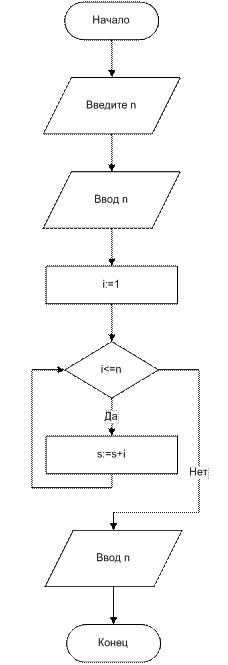
В теле цикла могут размещаться любые алгоритмические конструкции, в том числе и другие циклы.

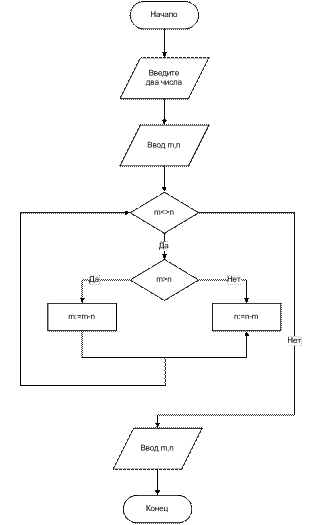
Пример. Составить блок-схему алгоритма вычисления наибольшего общего делителя двух чисел (алгоритм Евклида).

Опишем данный алгоритм на псевдокоде

1. Ввести два числа m и n

2. Пока m<>n делать

2.1 Если m>n, то m=m-n, иначе n=n-m

2.2 Перейти к шагу 2

3. Вывести m

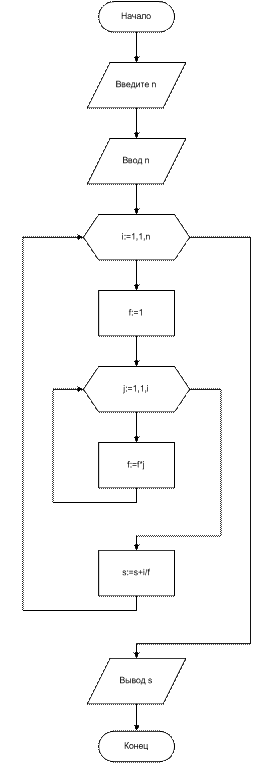
Если в тело цикла вкладывается другой цикл, то образуются вложенные циклы. Рассмотрим работу вложенных циклов на примере вычисления суммы последовательности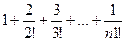

Помимо трех рассмотренных типов алгоритмов существуют еще также рекурсивные алгоритмы. Рекурсивным называется алгоритм, который в процессе своего выполнения прямо или косвенно обращается сам к себе.

Рекурсия может быть простой и сложной. Простой называется рекурсия, когда алгоритм вызывает себя непосредственно из себя же самого. Сложной называется рекурсия, когда алгоритм вызывается через другой алгоритм (например, алгоритм A вызывает алгоритм B, а алгоритм B вызывает алгоритм A). Количество вложенных вызовов называется глубиной рекурсии. Порождение новых копий рекурсивной подпрограммы до выхода на граничное условие называется рекурсивным спуском. Завершение работы рекурсивных подпрограмм, вплоть до самой первой, инициировавшей рекурсивные вызовы, называется рекурсивным подъёмом.

В рекурсивном определении должно присутствовать ограничение, граничное условие, при выходе на которое дальнейшая инициация рекурсивных обращений прекращается.

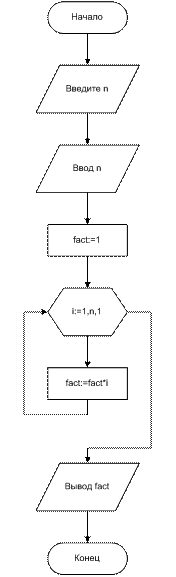
Рассмотрим рекурсивные алгоритмы на примере алгоритма вычисления факториала числа.

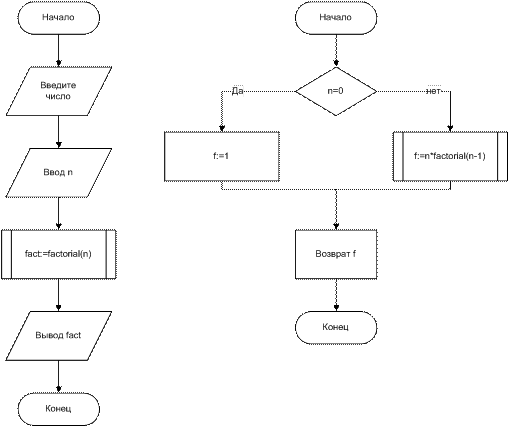
Без рекурсии

С рекурсией

В математике факториал числа определяется следующим образом:

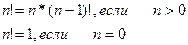
Факториал равен числу n, умноженному на факториал числа (n-1), который в свою очередь равен числу (n-1), умноженному на факториал числа (n-2) и т.д., пока вычисление не дойдет до 0!, который по определению равен 1.

Таким образом, факториал описан с помощью самого же себя, т.е. он подходящий кандидат на реализацию с помощью рекурсии.

С точки зрения компьютера на самом деле не имеет значения, вызывает ли алгоритм сам себя или другой алгоритм. Когда один алгоритм вызывает другой, то выполнение вызывающего алгоритма приостанавливается до тех пор, пока не будет выполнен вызываемый алгоритм. После вычисления результата (его значение передается вызывающему алгоритму) завершается выполнение вызываемого алгоритма и возобновляется выполнение вызывающего.

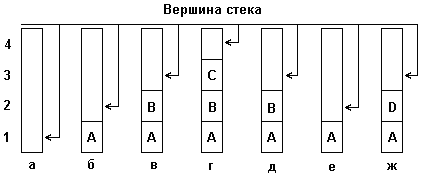
Каждый раз, когда один алгоритм вызывает другой, информация об его собственном состоянии должна быть сохранена в памяти, чтобы позднее завершить его выполнение. Помимо всего прочего эта информация содержит значения переменных в момент прерывания. Область памяти, в которой хранится эта информация, называется стеком (stack). Стек – это защищенная область системной памяти, с которой работает только операционная система. Память, отведенная для стека, это обычная память, но операционная система работает с ней не так, как с остальной памятью. Во-первых, другие программы не могут получить доступ к любому из байтов информации, хранящейся в стеке. Во-вторых, информация записывается в стек особым образом. Когда программа помещает значение в стек, новая информация записывается в его вершину. При чтении значения из стека программа читает содержимое самой верхней ячейки (заполненной в последнюю очередь). Такой тип организации памяти называют LIFO (Last-In-First-Out, последним пришел-первым вышел).

Не нашли, что искали? Воспользуйтесь поиском: