Общая схема построения графика функции

Постановка задачи. Исследовать функцию и построить ее график.

План решения.

1. Находим область определения функции .

2. Выясняем четность функции.

Если , то функция называется четной. График четной функции симметричен относительно оси ординат (оси ).

Если 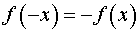, то функция называется нечетной. График нечетной функции симметричен относительно начала координат.

3. Выясняем периодичность функции.

Если при некотором , то функция называется периодической. График периодической функции имеет одну и ту же форму на каждом из отрезков . Поэтому достаточно построить график на каком-нибудь одном таком отрезке и затем воспроизвести полученную кривую на остальных отрезках

4. Находим точки максимума и минимума функции и интервалы возрастания и убывания (интервалы монотонности). Для этого:

вычисляем производную и находим критические точки функции, т.е. точки, в которых 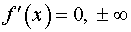или не существует;

определяя знак производной, находим интервалы возрастания и убывания функции: если 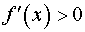, то функция возрастает, если , то функция убывает;

если производная меняет знак при переходе через критическую точку , то – точка экстремума: если производная меняет знак с «минуса» на «плюс» – то точка минимума, если же с «плюса» на «минус» – то точка максимума. Если производная сохраняет знак при переходе через критическую точку, то в этой точке экстремума нет.

5. Находим точки перегиба функции и интервалы выпуклости и вогнутости. Для этого:

вычисляем вторую производную и находим точки, принадлежащие области определения функции, в которых или не существует;

определяя знак второй производной, находим интервалы выпуклости и вогнутости: если , то функция выпукла, если , то функция вогнута;

если вторая производная меняет знак при переходе через точку , в которой или не существует, то – точка перегиба.

6. Находим асимптоты функции.

а) Вертикальные: находим односторонние пределы в граничных точках

и/или .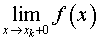

Если хотя бы один из этих пределов бесконечен, то – вертикальная асимптота графика функции .

б) Наклонные: если существуют конечные пределы

и ,

то прямая – наклонная асимптота графика функции (если , , то – горизонтальная асимптота).

Замечание 1. Асимптоты при и 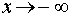могут быть разными.

Замечание 2. При необходимости можно найти точки пересечения кривой с осями координат и задать дополнительные точки.

7. Строим график функции.

Задача 7. Провести полное исследование функций и построить их графики.

.

1. Область определения: .

2. Функция ни четна, ни нечетна, т.к.

.

3. Функция не является периодической.

4. Интервалы возрастания и убывания.

.

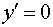при ; не существует при .

				не сущ.
				не сущ.

Функция убывает при .

Функция возрастает при .

– точка минимума.

5. Выпуклость и вогнутость кривой.

.

при ; не существует при .

– кривая выпукла;

– кривая вогнута;

– кривая вогнута.

– точка перегиба.

6. Асимптоты.

а) вертикальные: .

б) наклонные: ,

, .

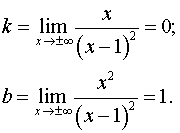
– наклонная (горизонтальная) асимптота.

7. График.

Не нашли, что искали? Воспользуйтесь поиском: