
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Численное решение задачи оптимизации управления
Предположим, что функционал (6) обладает особенностями: 1) имеет только один минимум (локальный, он же и абсолютный) на интервале определения k; 2) может не удовлетворять требованиям непрерывности и существования производной на интервале определения k. Функции, удовлетворяющие этим требованиям, называются унимодальными. Поиск минимума унимодальных функций может проводиться методом перебора, методом дихотомии, методом золотого сечения и методом чисел Фибоначчи [4]. Методы перечислены в порядке увеличения эффективности поиска. Таким образом, метод чисел Фибоначчи является самым эффективным. Поэтому поиск минимума функционала (6) будем проводить этим методом.
Реализация метода связана с использованием последовательности целых чисел, открытой итальянским математиком Леонардом Пизанским (Фибоначчи) в начале XIII века. Обозначим унимодальную целевую функцию через z = z (x). Необходимо найти точку х * при которой целевая функция z имеет минимум: z *= z (x *)=  z (x). При этом считаем, что х лежит в интервале [0, 1], поскольку любой другой интервал легко приводится к интервалу [0, 1].
z (x). При этом считаем, что х лежит в интервале [0, 1], поскольку любой другой интервал легко приводится к интервалу [0, 1].
Чтобы проследить за ходом развития схемы поиска х *, z *, предположим, что в нашем распоряжении имеется N экспериментов. Оценим ситуацию, которая возникает после того, как проведён N –1 эксперимент и остаётся выбрать последнее значение х = xN. К этому моменту гарантированная длина интервала неопределённости становится равной LN –1, а сам интервал содержит точку хN –1 (рис.3), причём среди всех величин zq (q =  ), полученных в предшествующих экспериментах, наибольшей является именно zN –1. Положение хN –1 на отрезке LN –1 зависит от того, какой метод поиска была реализована на предыдущих шагах.
), полученных в предшествующих экспериментах, наибольшей является именно zN –1. Положение хN –1 на отрезке LN –1 зависит от того, какой метод поиска была реализована на предыдущих шагах.
Длина конечного интервала неопределенности будет определяться не только выбираемым хN, но и уже имеющимся хN –1. Очевидно, результат поиска окажется наилучшим тогда, когда хN –1 расположится на расстоянии ε/2 от середины LN –1 (рис.3) (в этом случае достаточно разместить точку хN симметрично хN –1 и найти LN =(LN –1+ε)/2 независимо от того, в каком отношении находятся zN и zN –1). Таким образом, первым требованием к исследуемой схеме является следующее: после проведения N –1 экспериментов точка хN –1 должна занять на LN –1 положение, указанное на рис.3.
 | |||
 | |||
Рис.3. Рис.4.
|
|
|
|



|



|





|


|



|
|

 Пусть теперь стоит задача выбора двух последних значений х (xN –1 и xN) в условиях, когда N –2 эксперимента проведены и найден интервал LN –2 , содержащий точку xN –2 , в которой получено значение z=zN –2 , наилучшее (по смыслу задачи) в рассматриваемой серии опытов (рис.4). Начнём выбирать xN –1 (внутри LN –2); как только xN –1 и соответствующее zN –1 станут известны, можно будет указать новый интервал неопределённости, меньший LN –2. Поскольку заранее нельзя предсказать, будет ли zN –1> zN –2, лучше всего расположить точку xN –1 симметрично xN –2 несмотря на то, что рас-
Пусть теперь стоит задача выбора двух последних значений х (xN –1 и xN) в условиях, когда N –2 эксперимента проведены и найден интервал LN –2 , содержащий точку xN –2 , в которой получено значение z=zN –2 , наилучшее (по смыслу задачи) в рассматриваемой серии опытов (рис.4). Начнём выбирать xN –1 (внутри LN –2); как только xN –1 и соответствующее zN –1 станут известны, можно будет указать новый интервал неопределённости, меньший LN –2. Поскольку заранее нельзя предсказать, будет ли zN –1> zN –2, лучше всего расположить точку xN –1 симметрично xN –2 несмотря на то, что рас-
стояние между xN –1 и xN –2 окажется наверняка больше ε. Предложенный выбор xN –1 даёт гарантию того, что длина нового интервала неопределённости не превысит величины LN –1, отмеченной на рис.4, причем LN –1 не может быть уменьшена, если задана точка xN –2. Зная теперь xN –1 и помня о требовании, отражённом в рис.3, приходим к выводу: чтобы получить результат LN –1, необходимо два последних эксперимента провести так, как показано на рис.5, выполнив тем самым условие: LN –2 = LN –1+ LN.
  Таблица 1. Таблица 1.      
 Номер Номер
шага поиска q | Формула для интервала неопределённости Lq | ||||||||||||||
N –1 N –2 N –3 N –4 N –5 ∙ | LN = LN LN –1 = 2 LN – ε LN –2 = 3 LN – ε LN –3 = 5 LN – 2ε LN –4 = 8 LN – 3ε LN –5 = 13 LN – 5ε ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ | ||||||||||||||
| Lq = FN – q +1 LN – FN – q –1 ε |


 Если сделать очередной шаг и поставить задачу: найти xN –2, xN –1, xN при известных LN –3, xN –3, zN –3, то окажется, что рассуждения, приведенные выше, могут быть целиком перенесены и на этот случай. Таким образом, приходим к равенству LN –3 = LN –2 + LN –1; далее схема строится так, как показано на рис.6.
Если сделать очередной шаг и поставить задачу: найти xN –2, xN –1, xN при известных LN –3, xN –3, zN –3, то окажется, что рассуждения, приведенные выше, могут быть целиком перенесены и на этот случай. Таким образом, приходим к равенству LN –3 = LN –2 + LN –1; далее схема строится так, как показано на рис.6.
Теперь ясно, что основное соотношение, характеризующее метод, имеет вид
L q –1 = L q + L q +1 (q =  ). (16)
). (16)
Его анализ удобно начать с конкретизации выражений Lq (q = N, N— 1,...), сведя их в табл.1. Нетрудно заметить, что коэффициенты при LN и ε в формулах таблицы составляют последовательность чисел Фибоначчи (табл.2), задаваемую равенствами F 0 = F 1=1, Fk = Fk –1+ Fk –2, где k— номер числа Фибоначчи, принимающий значения 2, 3, …. Используя это обстоятельство, можно дать общую запись выражения Lq, приведённую в нижней строке табл.1, откуда сле-дует L 1 =FN LN – FN –2 ε. Но L 1 есть исходный единичный интервал неопределённости (L 1=1), поэтому [4]
LN = (l + ε FN –2 ) / FN. (17)
Таблица 2. Числа Фибоначчи.
| Число Фибоначчи Fk | |||||||||||||||||||||
| Номер числа Фибоначчи. k | |||||||||||||||||||||
| Число Фибоначчи Fk | 10 946 | ||||||||||||||||||||
| Номер числа Фиб. k | |||||||||||||||||||||
Соотношение (17) позволяет оценить эффективность метода чисел Фибоначчи. Большая эффективность метода чисел Фибоначчи связана с тем, что сокращение длины очередного интервала Lq требует проведения одного нового эксперимента, тогда как, например, в схеме дихотомии их требуется два.
Длина конечного интервала неопределённости LN должна быть меньше или равна 2ε. Из (17) следует
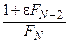 ≤ 2ε
≤ 2ε  1+ ε FN –2 ≤ 2ε FN
1+ ε FN –2 ≤ 2ε FN  ε(FN –2 –2 FN) ≤ –1
ε(FN –2 –2 FN) ≤ –1  ε(FN –2 –2 FN –1 –2 FN –2) ≤ –1
ε(FN –2 –2 FN –1 –2 FN –2) ≤ –1 
ε(– FN –2 –2 FN –1)≤–1  ε(FN –2 +2 FN –1)≥1
ε(FN –2 +2 FN –1)≥1  ε(FN –2 + FN –1+ FN –1) ≥ 1
ε(FN –2 + FN –1+ FN –1) ≥ 1  ε (FN + FN –1) ≥ 1
ε (FN + FN –1) ≥ 1  ε FN +1 ≥ 1.
ε FN +1 ≥ 1.
Отсюда следует
FN +1 ≤  . (18)
. (18)
Таким образом, конечное число шагов поиска N определяется по формуле (18).
В заключение рассмотрим вопрос о выборе точки х 1 и связанной с этим возможностью реализации метода. Из предыдущего анализа следует х 1=1– L 2; но L 2= FN –1 LN –ε FN –3 (см. табл. 1) или с учётом (17) L 2= FN [ FN –1+ε(FN -1 FN –2– FN FN –3)]. Отсюда следует, что сделать первый шаг здесь можно лишь тогда, когда назначено число N, т. е. х 1= х 1(N). Это является недостат-ком, затрудняющим в ряде случаев решение задачи из-за невозможности изменить N после начала экспериментов. Отметим, что метод золотого сечения не требует предварительного задания N и приближается по эффективности к исследованному методу чисел Фибоначчи [4].
Не нашли, что искали? Воспользуйтесь поиском:












 N
N