Інтерференція світла

V. ОПТИКА

Основні формули

1. Оптичний шлях променя

,

де – геометричний шлях про­меня у середовищі з показником заломлення .

2. Оптична різниця ходу двох променів, що поширюються у різ­них середовищах

3. Умова максимального під­силення світла внаслідок інтерфе­ренції

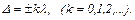
4. Умова максимального по­слаблення світла

Приклад розв'язання задачі

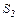Від двох когерентних джерел і промені довжиною хвилі потрапляють на ек­ран, на якому спостерігається інтер­ференційна картина. Коли на шляху одного з променів пер­пен­дикулярно до нього по­міс­тили мильну плівку n=1,33, ін­терференційна карти­на змі­ни­лась на протилежну. При якій найменшій товщині плівки це можливо?

Розв'язання

Зміна інтерференційної кар­ти­ни на протилежну означає, що на тих ділянках екрана, де спосте­рігались інтерференційні максиму-

ми, почали спостерігатись інтер­фе­ренційні мінімуми. Таке змі­щення інтерференційної картини можливе при зміні оптичної різ­ниці ходу пучків світлових хвиль на непарну кількість половин дов­жин хвиль, тобто

де – оптична різниця ходу світлових хвиль до внесення плів­ки; – оптична різниця ходу піс­ля внесення плівки;

Найменшій товщині плів­ки відповідає :

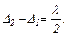
З рисунка отримуємо:

Тоді

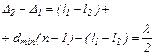
або

Звідси

Підставимо числові значення:

Задачі

33.1. Відстань від щілин до екрана в досліді Юнга Виз­начити відстань між щілинами, якщо на відрізку завдовжки укладається темних інтерференційних смуг. Довжина хвилі

33.2. Відстань між щілинами в досліді Юнга Яка відстань від щілин до екрана, якщо відстань між сусідніми темними сму­гами дорівнює ? Довжина хвилі світла Пристрій Юнга знаходиться в прозорій рідині з показником заломлення

33.3. В досліді Юнга на шляху одного з інтерференційних променів помістили тонку скляну пластинку з показником заломлення внаслідок чого центральна світла смуга змістилась в положення, яке займала спочатку п'ята світла смуга. Промінь світла падає перпен­дикулярно до поверхні пластинки. Довжина хвилі світла 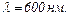Якою є товщина пластинки?

33.4. Визначити кут між дзеркалами Френеля, якщо відстань між інтерференційними смугами на екрані Ребро дзеркал знаходиться на відстані від паралельної йому щілини, яка є джерелом світла завдовжки і перебуває на відстані від екрана. Iнтерференційні промені падають на екран приблизно пер­пендикулярно.

33.5. Визначити найменшу товщину мильної плівки, якщо у від­битому світлі вона здається зеленою . Кут між нормаллю і променем зору . Показник заломлення плівки .

33.6. В яких межах може змінюватись товщина пластинки, щоб можна було спостерігати максимум порядку для довжини хвилі світла ? Показник заломлення пластинки .

33.7. На поверхню скляної пластинки, показник заломлення якої нанесено прозору плівку що освітлюється хвилею світла завдовжки що йде з повітря перпендикулярно до поверхні плівки. Яку найменшу товщину повинна мати плівка для того, щоб не було відбивання світла?

33.8. Мильна плівка з показником заломлення розміщена вертикально і утворює клин внаслідок стікання рідини. Під час спостереження інтерференційних смуг у відбитому світлі ртутної дуги виявилось, що відстань між п'ятьма смугами 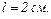Знайти кут клина. Світло падає перпендикулярно до поверхні плівки.

33.9. Поверхні скляного клина утворюють між собою кут 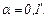На клин падає нормально до його поверхні пучок монохроматичних променів, довжина хвилі яких 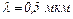Знайти лінійну відстань між темними інтерференційнми смугами.

33.10. Пристрій для отримання кілець Ньютона освітлюється моно­хроматичним світлом, яке падає нормально до поверхні пластинки. Спо­стереження ведеться у відбитому світлі. Радіуси двох сусідніх тем­них кілець і Радіус кривини лінзи Знайти порядкові номери кілець і довжину хвилі світла, що падає.

Дифракція світла

Основні формули

1. Дифракція Фраунгофера (у паралельних променях) на одній щілині:

умова мінімумів

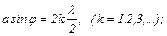
умова максимумів

де – ширина щілини; – кут дифракції.

2. Дифракція на решітці:

а) головні максимуми

де 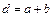– період решітки; – ширина непрозорих ділянок між щілинами; – ширина щілини;

де – кількість щілин на оди­ницю довжини решітки;

б) головні мінімуми

в) додаткові мінімуми

де 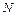– загальна кількість щілин.

Між двома головними макси­мумами розміщаються до­даткових мінімумів.

3. Роздільна здатність диф­ракційної решітки

де – найменша різниця дов­жини хвиль двох сусідніх спект­ральних ліній (l i l+Dl), при якій ці лінії можуть спостерігатись роздільно у спектрі, що отри­маний за допомогою даної решіт­ки; 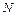– загальна кількість щілин решітки; – порядковий номер дифракційного максимуму.

Приклад розв'язання задачі

Скільки повних спектрів мож­на спостерігати за допомогою дифракційної решітки з штрихами на довжини, якщо ширина щілини дорівнює ширині проміжку між щілинами? Вважати, що повний спектр ви­димого світла з боку довго­хви­льового краю обмежений дов­жиною хвилі

Розв'язання

Визначимо сталу дифракцій­ної решітки:

За умовою . Кількість повних спектрів з кожного боку від спектра нульового порядку виз­нача­ється з умови:

або i

тобто .

Довгохвильові границі спект­рів визначаються за формула­ми:

Отже,

Внаслідок дифракції від од­нієї щілини на екрані утво­рю­ються мінімуми для променів, які поширюються під кутами до нор­малі, що визначаються рівнян­ням:

При виходить єдиний можливий мінімум, що відповідає куту , який визна­чається з рівняння:

тобто він збігається з кутом .

Звідси спектри другого по­рядку випадуть внаслідок диф­ракції від однієї щілини. На ек­рані буде видно два спектри – по одному з кожного боку від спект­ра нульо­вого порядку.

Задачі

34.1. Знайти радіуси перших п'яти зон Френеля, якщо відстань від дже­рела світла до хвильової поверхні відстань від хвильової поверхні до точки спостереження Довжина хвилі світла .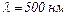

34.2. Знайти площу першої зони Френеля у випадку плоского фронту хвилі, якщо відстань від поверхні хвилі до точки спостереження а довжина світлової хвилі

34.3. На пластинку з щілиною, ширина якої падає нор­маль­но паралельний пучок променів з довжиною хвилі Дифракційне зображення щілини утворюється на екрані, розміщеному на відстані від пластинки. Знайти відстань між першою та другою темними лініями на екрані.

34.4. Період дифракційної решітки а ширина про­зорої частини 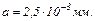Скільки максимумів не буде спосте­рігатися в спектрі по один бік від нульового максимуму до кута через вплив головних мінімумів ?

34.5. Дифракційна решітки містить щілин. Яка її ширина, якщо під кутом спостерігається 5000-й додатковий мінімум дифрак­ційної картини для жовтої лінії натрію з довжиною хвилі ?

34.6. Яку мінімальну кількість рисок повинна мати дифракційна решітка, щоб за допомогою неї можна було розділити лінії і жовтого дублета натрію, що має довжини хвиль i 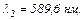якщо стала решітки ?

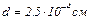34.7. Дифракційна решітка завдовжки має сталу Якою її роздільна здатність у спектрі другого порядку? Чому дорівнює різниця довжин двох найближчих хвиль, які розділяються у спектрі другого порядку, якщо довжина першої хвилі ?

34.8. На екрані отримано дифракційні спектри за допомогою дифракційної решітки, яка має штрихів на 1 мм довжини і яка розташована паралельно до екрана. Вважаючи, що граничні довжини хвиль, які сприймає людське око, i знайти ширину спектра першого порядку, якщо екран знаходиться на відстані від гратки.

34.9. На дифракційну решітку нормально падає монохроматичне світло з довжиною хвилі Кут між напрямами на максимуми першого і другого порядків . Визначити кількість штрихів на 1 мм дифракційної решітки.

34.10. На поверхню дифракційної решітки нормально до її поверхні падає монохроматичне світло. Стала дифракційної решітки в рази більша від довжини світлової хвилі. Знайти загальну кількість дифрак­ційних максимумів, які теоретично можна спостерігати в даному випадку.

Поляризація світла

Основні формули

1. Закон Брюстера

де – кут падіння, при якому відбита світлова хвиля повністю поляризована; – відносний показник заломлення.

2. Закон Малюса

де – інтенсивність світла, що пройшло через аналізатор; – інтенсивність світла, що падає на аналізатор; a – кут між голов­ними площинами поляризатора і аналізатора.

Приклад розв'язання задачі

Знайти кут між головними пло­щинами поляризатора і ана­лізатора, якщо інтенсивність при­родного світла, що пройшов че­рез поляризатор і аналізатор, змен­шилась в 4 рази.

Розв'язання

Позначимо інтенсивність при­родного світла . Після проход­ження через поляризатор промінь має інтенсивність

Після проходження через

аналізатор інтенсивність променя згідно із законом Малюса

де – кут між головними пло­щинами аналізатора і поляриза­тора.

За умовою

Тоді

Отже, .

Задачі

35.1. Граничний кут повного внутрішнього відбивання пучка світла на межі рідини з повітря . Визначити кут Брюстера для падіння променя з повітря на поверхню цієї рідини.

35.2. Промінь світла падає на поверхню рідини під кутом . Знайти кут заломлення променя, якщо відбитий промінь максимально поляризований.

35.3. Паралельний пучок світла переходить з гліцерину в скло 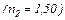так, що пучок, відбитий від межі поділу цих сере­довищ, стає максимально поляризованим. Визначити кут між залом­ле­ним пучком і пучком, що падає.

35.4. Пучок світла проходить із рідини в скло. Кут падіння пучка , кут заломлення . При якому куті падіння пучок світ­ла, відбитий від межі поaілу цих середовищ, буде максимально поляри­зованим?

35.5. Пучок світла падає на плоскопаралельну скляну пластину , нижня поверхня якої знаходиться у воді . При якому куті падіння світло, відбите від межі скло-вода, буде максимально поляризованим?

35.6. Кут максимальної поляризації при відбиванні світла від кристала кам'яної солі дорівнює . Визначити швидкість поши­рення світла в цьому кристалі.

35.7. Кут між головними площинами поляризатора і аналізатора . У скільки разів зменшиться інтенсивність світла, яке виходить із аналізатора, якщо кут збільшиться до ?

35.8. Промінь природного світла послідовно проходить через поляризатор і аналізатор, кут між головними площинами яких . Яка частка початкової інтенсивності світла буде на виході з аналізатора?

35.9. У скільки разів послаблюється природне світло, проходячи через два ніколі, головні площини яких утворюють між собою кут , якщо в кожному із них втрачається інтенсивності світла, що падає?

35.10. Кут між площинами поляризатора й аналізатора . Природне світло, проходячи через таку систему, ослаблюється в разів. Нехтуючи втратою світла під час відбиття, визначити коефіцієнт погли­нання світла в поляризаторі та аналізаторі.

Не нашли, что искали? Воспользуйтесь поиском: