ЭНЕРГИЯ, ЗАТРАЧЕННАЯ НА ПЕРЕМЕЩЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ

Рассмотрим свободную частицу с положительным зарядом Q в равномерном электрическом поле (рис.1.2.)

вставить рис. 1.5(Евдокимов, стр 16)

Рисунок 1.4

Эта частица будет перемещаться по направлению действующей на нее силы F_э. При перемещении частицы на пути l между точками 1 и 2 затрачивается энергия (совершается работа):

W₁,₂ =A_1,2= F_эl.

Учитывая формулу (1.2), выразим энергию через напряженность электрического поля Е:

W₁,₂ =A_1,2=EQl.

Работа при перемещении заряженной частицы совершается в результате силового взаимодействия частицы с внешним полем. Численно она пропорциональна напряженности поля и величине заряда.

Работа считается положительной, если заряженная частица перемещается по направлению сил поля, и отрицательной, если перемещение вызывается действием посторонних сил против направления сил электрического поля.

Аналогичные выводы можно сделать и для неравномерного поля, определяя работу при перемещении заряженной частицы между точками 1 и 2 как сумму элементарных значений работы dA, совершаемой на каждом бесконечно малом отрезке пути dl, в пределах которого напряженность поля можно считать постоянной:

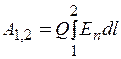(1.3)

где Е_п - проекция вектора напряженности поля на направление движения заряженной частицы.

Общая величина работы А на замкнутом пути 1-4-2-5-1 равна нулю:

(1.4)

Отсюда следует, что работа, совершаемая силами поля при перемещении заряженной частицы между двумя точками, не зависит от выбранного пути, а определяется положением начальной и конечной точек пути (1 и 2), т. е. расстоянием l.

1.4. ЭЛЕКТРИЧЕСКОЕ НАПРЯЖЕНИЕ. ПОТЕНЦИАЛ

Количество работы зависит не только от величин, относящихся к полю E,l, но и от заряда частицы Q. Поэтому с энергетической точки зрения поле вдоль рассматриваемого пути характеризуется работой, приходящейся на единицу заряда:

.

Это отношение называется электрическим напряжением.

Электрическое напряжение есть энергетическая характеристика поля вдоль рассматриваемого пути из одной точки в другую, которой оценивается возможность совершения работы при перемещении заряженных частиц между этими точками.

Нетрудно найти связь напряженности равномерного поля с напряжением между двумя любыми точками:

(1.5)

Единица электрического напряжения

[U] = [A/Q] = Джоуль/кулон = вольт(В)

Применяются также производные от вольта:

1 киловольт (кВ) = 10³ В;

1 милливольт (мВ)=10 ^-3 В;

1 микровольт (мкВ)=10 ^-6 В.

Учитывая, что работа, совершаемая при перемещении заряженной частицы в электрическом поле, зависит от положения начальной и конечной точек пути, для расчета можно ввести энергетическую характеристику поля в каждой точке, величина которой является функцией положения точки. Такой характеристикой является электрический потенциал.

Предположим, что пробная частица, обладающая зарядом Q, расположена в точке 1 электрического поля (см. рис. 1.2) и, следовательно, находится под действием силы F_э. Электрическое поле действует на эту частицу подобно тому, как действует на тело поле тяготения, т. е. частица обладает потенциальной энергией A₁

При перемещении заряженной частицы из точки 1 в точку 2 совершается работа A ₁,₂, связанная с действием той же силы F_э. Работу A ₁,₂ нужно рассматривать как убыль потенциальной энергии заряженной частицы при перемещении ее между указанными точками.

Следовательно, потенциальная энергия в точке 2

W₂ =W₁-W_1,2

Электрическим потенциалом поля называется отношение потенциальной энергии заряженной частицы, по­мещенной в данную точку электрического поля, к величине ее заряда в этой точке:

V₁=W₁/Q; V₂=W₂/Q.

Таким образом, напряжение между двумя точками электрического поля равно разности потенциалов поля в этих точках:

(1.6)

Аналогичные рассуждения можно привести, рассматривая заряженную частицу в точках 2, 3 и др.

Потенциальная энергия заряженной частицы в электрическом поле уменьшается при переходе от точки к точке по направлению линий напряженности. Она становится равной нулю за пределами электрического поля, где сила F_э = 0.

При наличии электрического поля бесконечной протяженности сила F_э равна нулю в бесконечности.

При обратном перемещении заряженной частицы против силы взаимодействия ее с электрическим полем потенциальная энергия будет возрастать за счет работы внешней неэлектрической силы.

Потенциальную энергию можно определить относительно какого-либо уровня, принятого за начальный. При теоретических исследованиях за начальный потенциал принимают потенциал бесконечно удаленной точки поля, где он равен нулю.

Таким образом, потенциал любой точки электрического поля характеризуется энергией, которая затрачивается (или может быть затрачена) на перемещение, единицы заряда из данной точки электрического поля в бесконечность (или наоборот).

При решении практических задач, относящихся к электрическим установкам, обычно полагают начальным потенциал земли, который принимают равным нулю.

Не нашли, что искали? Воспользуйтесь поиском: