Второй закон Кирхгофа

Алгебраическая сумма э.д.с. в любом контуре цепи равна алге­браической сумме падений напря­жения на элементах этого контура: .

Обход контура совершается в произвольно выбранном направ­лении, например по ходу часовой стрелки. При этом соблюдается сле­дующее правило знаков для э.д.с. и падений напряжения, входящих в (2): э.д.с. и падения напряже­ния, совпадающие по направлению с направлением обхода, берутся с одинаковыми знаками.

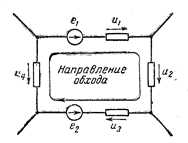Например, для данной схемы .Уравнение (2) можно перепи­сать так: . Здесь и — е — напряжение на ветви.

Следовательно, алгебраическая сумма напряжений на ветвях в лю­бом замкнутом контуре равна нулю.

Формулы (1) и (2) напи­саны в общем виде для мгновенных значений токов, напряжений и э.д.с; они справедливы для цепей как пе­ременного, так и постоянного тока.

Под напряжением на некотором участке электрической цепи понимается разность потенциалов между крайними точками этого участка, т.е.

(4)

Просуммируем напряжения на ветвях некоторого контура:

Поскольку при обходе контура потенциал каждой i -ой точки встречается два раза, причем один раз с “+”, а второй – с “-”, то в целом сумма равна нулю.

Таким образом, второй закон Кирхгофа математически записывается, как:

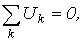
(5)

- и имеет место следующую формулировку: алгебраическая сумма напряжений на зажимах ветвей (элементов) контура равна нулю. При этом при расчете цепей с использованием законов Кирхгофа записывается независимых уравнений по второму закону Кирхгофа, т.е. уравнений, записываемых для контуров, каждый из которых отличается от других хотя бы одной ветвью. Значение топологического понятия “дерева”: дерево позволяет образовать независимые контуры и сечения и, следовательно, формировать независимые уравнения по законам Кирхгофа. Таким образом, с учетом (m-1) уравнений, составленных по первому закону Кирхгофа, получаем систему из уравнений, что равно числу ветвей схемы и, следовательно, токи в них находятся однозначно.

Введем столбцовую матрицу напряжений ветвей

U=

Тогда второй закон Кирхгофа в матричной форме записи имеет вид

В качестве примера для схемы рис. 5 имеем

,

откуда, например, для первого контура получаем

,

что и должно иметь место.

Если ввести столбцовую матрицу узловых потенциалов

=

причем потенциал последнего узла , то матрица напряжений ветвей и узловых потенциалов связаны соотношением

U=AТ

(7)

где A^Т - транспонированная узловая матрица.

Для определения матрицы В по известной матрице А = А _Д А _С, где А _Д – подматрица, соответствующая ветвям некоторого дерева, А_С - подматрица, соответствующая ветвям связи, может быть использовано соотношение В = (-А ^Т_С А ^-1Т_Д 1).

4) Типы задач, решаемых при расчёте электрооборудования. Дуальность элементов

В рамках электротехники решаются 2 задачи: анализ и синтез (проектирование).

При проектировании различного рода устройств ав­томатического управления, каналов электропроводной и радиосвязи и т. п. возникает необходимость подбора схем и параметров электрических цепей, отвечающих оп­ределенным требованиям. Нахождение схемы и элемен­тов цепи, удовлетворяющей заданным условиям, состав­ляет задачу синтеза электрической цепи.

Ввиду того что установившийся и переходный про­цессы во всякой линейной электрической цепи зависят от частотных свойств цепи, задача синтеза обычно сводится к нахождению цепи по заданной частотной харак­теристике. Искомым может быть двухполюсник с задан­ной зависимостью сопротивления (или проводимости) от частоты либо четырехполюсник с заданной передаточной функцией или частотной зависимостью его параметров. Построение схемы пассивной цепи по заданной частотной функции принято называть реализацией или осу­ществлением функции.

В отличие от задачи анализа, в которой искомая ве­личина — реакция цепи на приложенное воздействие — получается однозначно, задача синтеза может иметь не­сколько решений (или вовсе не иметь решения). Задан­ная частотная функция считается реализуемой или осу­ществимой, если соответствующая ей электрическая цепь может быть составлена из сопротивлений, индуктивностей и емкостей (возможно также применение трансфор­маторов).

Поскольку задача синтеза может иметь несколько ре­шений, возникает необходимость сопоставления получен­ных вариантов и выбора оптимального решения.

В этом вопросе не имеется вполне определенного критерия, так как приходится сравнивать схемы с разно­родными элементами. При этом обычно руководствуются следующими соображениями. Желательны схемы с наи­меньшим количеством элементов, имеющие практически приемлемые параметры, причем предпочтение следует от­давать схемам, содержащим простейшие элементы — сопротивления и емкости.

Индуктивность — менее желательный элемент цепи. Если в схеме последовательно включены индуктивность и сопротивление, то они могут быть практически выпол­нены в виде индуктивной катушки. Однако при этом приходится считаться с витковой емкостью, которая мо­жет внести в работу цепи искажения при высоких ча­стотах.

Еще менее желательным элементом схемы является трансформатор, практическое осуществление которого сопряжено с появлением тепловых потерь и межвитковых емкостей. Кроме того, коэффициент связи может не совпадать с расчетным.

В задачах синтеза частотные характеристики сопро­тивлений, проводимостей или передаточных функций мо­гут быть заданы графически или аналитически. Если характеристика задана графически или не является рациональной функцией, то она приближенно аппроксимирует­ся рациональной функцией, т. е. отношением двух поли­номов, которое по определенным правилам синтеза реа­лизуется в виде двух- или четырехполюсника.

Таким образом, первым этапом в задаче синтеза яв­ляется аппроксимация заданной частотной характери­стики рациональной функцией; этот этап, относящийся к области математики, здесь нерассматривается. Второй этап заключается в реализации рациональнойфункции, что и составляет основное содержание данной главы.

Не нашли, что искали? Воспользуйтесь поиском: