Способы соединения четырехполюсников

Каскадное соединение четырехполюсников. Каскадным соединением четырехполюсников называется такое соединение, при котором выход предыдущего четырехполюсника соединяется со входом последующего.

Рис. 5.3. Схема каскадного соединения двух четырехполюсников.

На рис. 5.3 показано каскадное соединение двух четырехполюсников, которые заданы своими матрицами А-параметров:

. (5.59)

Зная матрицы двух четырехполюсников (5.59) запишем их уравнения передачи в А-параметрах в матричном виде, используя обозначения, приведенные на рис. 5.3:

, (5.60)

, (5.61)

Из схемы рис. 5.3 видно, что

,

поэтому выражение (5.60) можно записать в следующем виде:

. (5.62)

Из выражения (5.62) видно, что при каскадном соединении четырехполюсников матрица А-параметров результирующего четырехполюсника равна произведению одноименных матриц соединенных четырехполюсников, т.е.:

. (5.63)

Последовательное соединение четырехполюсников. Последовательное соединение двух четырехполюсников, заданных матрицами Z-параметров, показано на рис.5.4.

Рис. 5.4 Схема последовательного соединения четырехполюсников.

Из рис. 5.4 видно, что и .

Уравнения передачи четырехполюсников Z ′ и Z ″ в матричном виде имеют вид:

, (5.64)

. (5.65)

Складывая матричные уравнения (5.64) и (5.65) получим:

. (5.66)

Из выражения (5.66) видно, что при последовательном соединении четырехполюсников матрица Z-параметров результирующего четырехполюсника равна сумме одноименных матриц соединенных четырехполюсников, т.е.:

(5.67)

Параллельное соединение четырехполюсников. Параллельное соединение четырехполюсников заданных матрицами Y- параметров показано на рис. 5.5.

Рис. 5.5 Схема параллельного включения двух четырехполюсников.

Из схемы видно, что:

; ;

; .

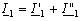Записывая уравнения передачи в Y-параметрах в матричном виде для каждого четырехполюсника и суммируя матричные уравнения, доказывается, что Y-матрица результирующего четырехполюсника равна сумме одноименных матриц соединенных четырехполюсников, т.е.:

(5.69) Смешанное соединение четырехполюсников. Схема смешанного соединения двух четырехполюсников, заданных матрицами Н-параметров приведена на рис. 5.6.

Рис.5.6. Схема смешанного соединения двух четырехполюсников.

Записав уравнения передачи в Н-параметрах для каждого четырехполюсника в матричном виде и складывая полученные матричные равенства можно доказать, что при смешанном соединении четырехполюсников матрица Н-параметров общего четырехполюсника получается путем суммирования одноименных матриц соединяемых четырехполюсников, т.е.:

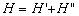(5.70)

34) Принципы согласования нагрузки. Характеристические (вторичные) параметры четырёхполюсников и их связь с первичными параметрами

В электросвязи широко используется режим работы симметричного четырехполюсника, при котором его входное сопротивление равно нагрузочному, т.е.

.

Это сопротивление обозначают как и называют характеристическим сопротивлением симметричного четырехполюсника, а режим работы четырехполюсника, для которого справедливо

,

называется режимом согласованной нагрузки.

В указанном режиме для симметричного четырехполюсника на основании (3) и (4) можно записать

;

(13)

.

(14)

Разделив соотношение (13) на (14), получаем уравнение

,

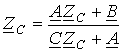решением которого является

.

(15)

С учетом (15) уравнения (13) и (14) приобретают вид

;

.

Таким образом,

,

где - коэффициент распространения; - коэффициент затухания (измеряется в неперах); - коэффициент фазы (измеряется в радианах).

Одному неперу соответствует затухание по напряжению или току в е=2,718… раз, а по мощности, поскольку для рассматриваемого случая в е2 раз.

Запишем уравнение симметричного четырехполюсника с использованием коэффициента распространения.

По определению

.

(16)

Тогда

.

(17)

Решая (17) и (18) относительно и , получим

и .

Учитывая, что

и

,

получаем уравнения четырехполюсника, записанные через гиперболические функции:

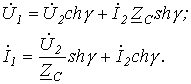
35) Экспериментальное определение первичных и вторичных параметров четырёхполюсников

Если схема четырехполюсника неизвестна, то его параметры можно определить экспериментальным путем, используя режимы холостого хода и короткого замыкания.

Рис. 5.9. Схема для экспериментального определения параметров четырехполюсника.

Определим А-параметры четырехполюсника.

Для этого на входе четырехполюсника подключим вольтметр (V), амперметр (А) и фазометр (φ), как показано на рис. 5.9.

Переведем четырехполюсник в режим холостого хода по выходу (I2=0) и измерим с помощью приборов Iх.х.1, Uх.х.1 и φх.х.1.

В случае, когда I2 = 0 система А-параметров имеет вид:

(5.76)

Из (5.76) получим

. (5.77)

Переведем четырехполюсник в режим короткого замыкания по выходу (U2 = 0). Измерим Iк.з.1, Uк.з.1 и φк.з.1, тогда система А-параметров будет иметь вид:

(5.78)

Из (5.78) получим

. (5.79)

Подключим приборы к зажимам (2-2) и переведем четырехполюсник в режим холостого хода по входу (I1 = 0) и измерим Iх.х.2, Uх.х.2 и φх.х.2. Тогда имеем:

(5.80)

Из (5.80) получим

. (5.81)

Четвертое уравнение получим, используя соотношение:

. (82)

Решив систему уравнений (5.77), (5.79), (5.81) и (5.82), найдем А-параметры:

; ;

; .

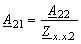37) Транзистор как четырёхполюсник

Не нашли, что искали? Воспользуйтесь поиском: