Принцип действия синхронной машины

Статор 1 синхронной машины (рис. 1.1, а) выполнен так же, как и асинхронной: на нем расположена трехфазная (в общем случае многофазная) обмотка 3. Обмотку ротора 4, которая питается от источника постоянного тока, называют обмоткой возбуждения, так как она создает в машине магнитный поток возбуждения.

Рис. 1.1 – Электромагнитная схема синхронной машины (а) и схема ее включения (б):

1 – статор, 2 – ротор, 3-обмотка якоря, 4 – обмотка возбуждения,

5 – контактные кольца, 6 – щетки

Вращающуюся обмотку ротора соединяют с внешним источником постоянного тока посредством контактных колец 5 и щеток 6. При вращении ротора 2 с некоторой частотой n ₂ поток возбуждения пересекает проводники обмотки статора и индуктирует в ее фазах переменную э. д. с. E (рис. 1.1, б), изменяющуюся с частотой

f₁ =pn₂ /60 (1.1)

Если обмотку статора подключить к какой-либо нагрузке, то протекающий по этой обмотке многофазный ток I_a создаст вращающееся магнитное поле, частота вращения которого

n₁ =60f₁ /p. (1.2)

Из (1.1) и (1.2) следует, что n ₁ = n ₂, т.е. ротор вращается с той же частотой, что и магнитное поле статора. По этой причине рассматриваемую машину называют синхронной. В такой машине результирующий магнитный поток Ф_рез создается совместным действием м. д. с. обмотки возбуждения и обмотки статора и результирующее магнитное поле вращается в пространстве с той же частотой, что и ротор.

При холостом ходе магнитный поток генератора создается обмоткой возбуждения, причем он направлен по оси полюсов ротора и индуцирует в фазах обмотки якоря ЭДС.

Электродвижущая сила. Первая гармоническая этой ЭДС определяется по той же формуле, что и первая гармоническая ЭДС для асинхронной машины:

E ₀ = 4,44 f_lw_ak_{o 6 a} Ф _B, (8.3)

где w_a и к_о6а — число витков в фазе и обмоточный коэффициент обмотки якоря; Ф_в — поток первой гармонической магнитного поля возбуждения.

Методы расчёта сложных цепей

1) Метод эквивалентного генератора напряжения

Метод эквивалентного генератора напряжения позволяет определить ток в

любой ветви сложной цепи,не определяя истинных токов в других ветвях.

Ток,согласно этому методу,определяется по формуле:

I_н= U_нхх /(R_вн+ R_н) (2.1)

где R_вн- внутреннее сопротивление генератора,

R_н- сопротивление ветви,ток в которой рассчитывается,

U_нхх- напряжение эквивалентного генератора,определяется как напряжение в ветви при её обрыве.

Внутреннее сопротивление можно определить:

а) экспериментально,используя зависимость (2.1),если закоротитьR_н(R_н=0). Тогда: I_нкз = U_нхх/R_вн следовательно: R_вн =U_нхх/I_нкз

б) аналитически,расчётным путём, исключив из схемы все ЭДС,но оставив

их внутренние сопротивления,преобразовать схему к одному сопротивле-

нию R_внотносительно точек разрыва.

2) Метод двух узлов

Часто встречаются схемы, содержащие только два узла. Наиболее рациональным методом расчёта токов в такой схеме является метод двух узлов. В данном методе за искомое принимается напряжение между двумя узлами схемы. Узловое напряжение определяется по формуле:

U_abES= (_nC_nS+ I _nGS)/_m(2.2)

ESгде _nC_n- алгебраическая сумма произведений ЭДС ветвей на проводимо-

сти этих ветвей;

I_n- токи источников тока;

GS_m - сумма проводимостей всех ветвей,соединяющих узлыa иb.

После того,как определено узловое напряжение ток в любой ветви находится на основе обобщённого закона Ома.

3) Метод узловых напряжений

Метод узловых напряжений основан на применении первого закона Кирхгофа и закона Ома для участков цепи.Сущность метода сводится к определению узловых напряжений относительно некоторого базисного узла. Если принять потенциал базисного узла равным нулю,то напряжения между остальными узлами

и базисным узлом будут равны потенциалам этих узлов.Зная узловые напряжения ветвей,по закону Ома легко определить токи ветвей.

1) Метод узловых потенциалов позволяет уменьшить число со­вместно решаемых независимых уравнений для расчета цепи до Y - 1, где Y— число узлов схемы замещения цепи. Метод основан на применении первого закона Кирхгофа и заключается в следу­ющем.

1. Один узел схемы цепи принимаем базисным "с нулевым по­тенциалом. Такое допущение не изменяет разности потенциалов между узлами, а следовательно, напряжения и токи ветвей.

2. Для остальных Y-1 узлов составляем уравнения по первому закону Кирхгофа,.выражая токи ветвей через потенциалы узлов.

3. Решением составленной системы уравнений определяем по­тенциалы Y- 1 узлов относительно базисного, а затем токи ветвей по обобщенному закону Ома

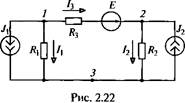
Рассмотрим расчет цепи, содержащей Y= 3 узла (рис. 2.22). Узел 3 принимаем базисным, т.е. потенциал К₃ = 0. Из уравнений по первому закону Кирхгофа для узлов 1 и 2

I₁+ I₃+ J₁=0;

I₂- I₃- J₂=0;

после подстановки выражений токов через потенциалы узлов

Решение системы

2). Метод Контурных Токов. Метод контурных токов позволяет уменьшить число совместно решаемых независимых уравнений для расчета схемы цепи до К= В- Bj- Y+ I и основан на применении второго закона Кирхгофа.

Рассмотрим сначала расчет схемы цепи без источников тока, т.е. при Bj=0, а затем общий случай.

Схема цепи без источников тока. Метод контурных токов для расчета схемы цепи без источников тока заключается в следующем.

1. Выбираем К=В- Y+ 1 независимых контуров и положитель-
ных направлений контурных токов, каждый из которых протекает
по всем элементам соответствующего контура.

Для планарных схем, т.е. допускающих изображение на плос­кости без пересечения ветвей, достаточным условием выделения А'независимых контуров является наличие в каждом из них одной ветви, принадлежащей только этому контуру.

Для К независимых контуров составляем уравнения по вто­рому закону Кирхгофа, совместное решение которых определяет все контурные токи.

Ток каждой ветви определяем по первому закону Кирхгофа как алгебраическую сумму контурных токов в соответствующей ветви.

Рассмотрим расчет цепи (рис. 2.25, а) с числом ветвей В= 6, узлов Y= 4, независимых контуров К- В- Y+ 1=6-4+1 = 3.

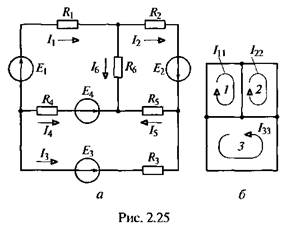
Выберем независимые контуры 1—3 и положительные направле­ния контурных токов в них Iц,I₂₂ и I₃₃ (рис. 2.25, б). В отличие от токов ветвей каждый контурный ток обозначим двойным индек­сом номера контура.

Составим систему уравнений по второму закону Кирхгофа для контуров 7, 2 и 3:

решение которой определяет контурные токи Iц,I₂₂ и I₃₃

Токи ветвей (см. рис. 2.25, а) при выбранных для них положи­тельных направлениях находим по первому закону Кирхгофа I₁=I₁₁, I₂=I₂₂, I₃=I₃₃, I₄=-I₁₁ –I₃₃, I₅=I₂₂+I₃₃, I₆=I₁₁ –I₂₂

Все.

Не нашли, что искали? Воспользуйтесь поиском: