Раздел 2. Оценка параметров и доверительных интервалов зависимости

1.Среднесуточная продажа хлеба в течение многих лет для данного магазина составляла 6 т при среднем квадратичном отклонении 0,05т. Сегодня магазином было продано 7 т хлеба. Можно ли при 5%-м уровне значимости предполагать, что и завтра будет продано 7 т хлеба?

2. Фирма-изготовитель женских украшений, выпустив новый товар, утверждает, что 40% покупателей купят эти украшения. В ходе 10-дневной рекламной распродажи в среднем приобрели украшения 29,5% покупателей, выборочное среднее квадратичное отклонение составило 16,5%. При 5%-м уровне значимости оценить утверждение изготовителя товара.

3. Поставщик двигателей утверждает, что средний срок их службы равен 800ч. Для выборки из 17 двигателей средний срок службы оказался равным 865 ч при выборочном среднем квадратичном отклонении 120ч. Проверить нулевую гипотезу при уровне значимости: а)5%; б) 1%.

4. По результатам 10 замеров установлено, что среднее время обслуживания мастером клиента мин. Предполагая, что время обслуживания клиента – нормально распределенная случайная величина с дисперсией мин , при уровне значимости установить, можно ли принять в качестве норматива (математического ожидания) для обслуживания одного клиента: а) 21 мин; б) 16 мин.

5. Поставщик удобрений утверждает, что применение новой партии удобрений обеспечивает урожайность пшеницы в 60ц/га. Удобрения внесли на площади в 37 га и получили урожай 55 ц/га при выборочном среднем квадратичном отклонении 3ц/га. При 5%-м уровне значимости оценить справедливость утверждения поставщика.

6. Составлена случайная выборка из 64 покупателей, которые интересовались товаром А. Из них товар А купили 16 человек. Поставщик утверждает, что данный товар должен привлечь треть покупателей, а среднее квадратическое отклонение 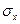равно одному человеку. Проверить нулевую гипотезу при 5%-м уровне значимости.

7. Среднесуточная продажа подсолнечного масла в течение многих лет для данного магазина составляла 500л при среднем квадратичном отклонении 0,5л. Сегодня магазином было продано 530 л подсолнечного масла. Можно ли при 5%-м уровне значимости предполагать, что и завтра будет продано 530 л подсолнечного масла?

8. Фирма по изготовлению электрофенов в рекламном буклете утверждает, что средний срок безотказной работы предлагаемого изделия – 1500ч. Для выборки из 100 фенов средний срок безотказной работы оказался равным 1420 ч при выборочном среднем квадратитчном отклонений 100ч. При 5%-м уровне значимости проверить гипотезу о том, что значение 1500ч является математическим ожиданием.

9. Ювелирная фабрика выпустив новый товар, утверждает, что 20% покупателей купят эти украшения. В ходе месячной рекламной распродажи в среднем приобрели украшения 15,3% покупателей, выборочное среднее квадратичное отклонение составило 6,8%. При 5%-м уровне значимости оценить утверждение изготовителя товара.

10. Фармацевтическая фирма утверждает, что применение нового лекарства гарантирует выздоровление больных в 60 случаях из 100. Лекарство апробировано на 30 больных и выздоровление зарегистрировано в 55 случаях при выборочном среднем квадратичном отклонении 3 человека. При 5%-м уровне значимости оценить справедливость утверждения фирмы.

11. На двух станках производят одну и ту же продукцию, контролируемую по наружному диаметру изделия. Из продукции станка А было проверено 20 изделий, а из продукции станка В - 25 изделий. Выборочные оценки математических ожиданий и дисперсий контролируемых размеров составили = 37,5 мм при = 1.21 мм² и 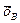= 36,08 мм при = 1,44 мм². Проверить гипотезу о равенстве дисперсий.

12. Фирма-поставщик в рекламном буклете утверждает, что средний срок безотказной работы предлагаемого изделия – 2900ч. Для выборки из 50 изделий средний срок безотказной работы оказался равным 2720 ч при выборочном среднем квадратитчном отклонений 700ч. При 5%-м уровне значимости проверить гипотезу о том, что значение 2900ч является математическим ожиданием.

Мемлекеттік емтиханның бақылау сұрақтарының

ТІЗІМІ

5В070300- «Ақпараттық жүйелер»

Не нашли, что искали? Воспользуйтесь поиском: