
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Изучение движений маятника Фруда
Лабораторная работа № 13.
1. Цель работы: закрепление теоретических знаний по теме 3.7. “Автоколебания и параметрические колебания”
приобретение практических навыков работы с колебательными системами, имеющими несколько режимов колебаний,
изучение методики расчетов таких систем
2. Порядок подготовки к выполнению работы: изучить тему и материал лабораторной работы
3. Порядок выполнения лабораторной работы в соответствии с режимами колебаний маятника
4. Подведение итогов выполнения работы:
предъявить результаты, подготовка и оформление отчета, заполнить таблички, произвести обработку результатов измерений
5. техника безопасности при выполнении лабораторной работы стандартная с электрическими цепями
Цель работы: изучить различные режимы движения маятника Фруда.
Оборудование: маятник Фруда, источник питания с регулирующим напряжением.
Теория
Режимы работы осциллятора при подводе к нему энергии. Маятник Фруда и ламповый генератор
Н. Е. Жуковским было предложено устройство совершенного (без потерь) подвеса маятника, схематически показанное на рис. 48. Муфта A, насаженная на вал С, составляет одно целое с маятником В. Вал расположен горизонтально и равномерно вращается с угловой скоростью ω, маятник совершает колебания в плоскости, перпендикулярной к валу.
Можно показать, что если угловая скорость вала достаточно велика и сила трения муфты о вал не зависит от скорости скольжения, то потери энергии колебаний в подвесе не будет. Рассмотрим, как велика должна быть угловая скорость вращения вала.
Второй закон Ньютона для вращательного движения имеет вид:
Je = Mтр-Мтяж, Мтяж = mg a sinφ, (163)
где а - расстояние от оси вращения до центра масс, φ - угол отклонения маятника от вертикали, m - масса маятника, g - ускорение свободного падения, e - угловое ускорение маятника, J - момент инерции маятника.
Момент силы тяжести в процессе движения меняет свой знак.
Момент силы трения равен: Mтр = RFтр,
где R - радиус вала, Fтр - величина силы трения скольжения
Fтр = m Р, μ - безразмерный коэффициент трения, P – сила давления маятника на ось. Из рисунка рис. 48 следует: Р = mg co sφ.
 |
Тогда Fтр = mmg cosφ; a Mтр = Rmmg cos
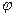 (164)
(164)

Рис. 1. Маятник Фруда
Если предположить, что вал вращается по часовой стрелке, то момент силы тяжести на рисунке направлен от нас перпендикулярно плоскости чертежа.
Относительно оси ОХ он будет отрицательным, а момент силы трения положительным.
Подставив значение величин в формулу (163) получаем:
Jε+ mga sin φ = Rmmg cosφ.
Это уравнение будет уравнением гармонических колебаний при условии, что амплитуда колебаний A = а | sinφm | значительно меньше характерной длины маятника а, где φm - -угол максимального отклонения маятника от положения равновесия.
a | sinφm | << a, | sinφm | << 1
При таком условии cos φ = 1 sin φ  φ, а уравнение колебаний принимает вид:
φ, а уравнение колебаний принимает вид:
J 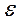 + mga φ = Rmmg (165)
+ mga φ = Rmmg (165)
В уравнении (163) ε = 
Преобразуем (163) к виду:
 +
+  φ =
φ =  (166)
(166)
Величин  = w
= w  , где ω0 - частота собственных гармонических колебаний маятника.
, где ω0 - частота собственных гармонических колебаний маятника.
Рассмотрим, каким образом изменится характер колебаний маятника, если сила трения муфты о вал (рис.48) будет зависеть от скорости скольжения муфты по валу при сохранении остальных условий предыдущей задачи.
Рассмотреть два случая:
1) сила трения возрастает с увеличением скорости скольжения
2) сила трения уменьшается с увеличением скорости скольжения.
Случай.
В этом случае относительная угловая скорость вращения муфты и вала wв равна:
wв = w - wm,
где wm =  - угловая скорость маятника..
- угловая скорость маятника..
Сила трения в этом случае равна:
Fтр = k (w - wm),
где k - постоянный множитель, а уравнение колебаний (166), которое следует из предыдущей задачи, примет вид:
J 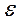 + mga φ = R k (w -
+ mga φ = R k (w -  ) (167)
) (167)
откуда получим:
 +
+  φ+
φ+ 
 =
=  w, (168)
w, (168)
или
 +2β
+2β 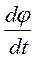 +ω
+ω  φ = С,. (169)
φ = С,. (169)
где β =  - коэффициент затухания., w
- коэффициент затухания., w  =
=  - частота незатухающих гармонических колебаний маятника, С =
- частота незатухающих гармонических колебаний маятника, С =  - постоянная величина.
- постоянная величина.
Решение уравнения (169), как и ранее, состоит из суммы решений частного решения неоднородного уравнения (169):
φ1 = 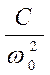
и общего решения однородного уравнения:
 +2
+2 
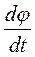 +
+ 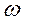
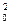
 = 0. (170)
= 0. (170)
В теории колебаний показано, что общее решение однородного уравнения (170) имеет вид:
φ2 = φmexp (-βt)cos (ωв t+a).
Таким образом
φ = φ1+φ2 =  + φmexp (-βt)cos (ωв t+a) (171)
+ φmexp (-βt)cos (ωв t+a) (171)
Из приведенного уравнения следует, что в этом случае колебания происходят около смещенного положения равновесия и затухают.
Случай.
В этом случае следует считать, что: Fтр =  =
=  .
.
Учитывая, что ωм / ω << 1, получаем:
Fтр 
 (1+
(1+  )
)
Уравнение колебаний в этом случае принимает вид:
J 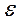 + mga φ = R
+ mga φ = R  (1+
(1+  ),
),
или J 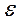 + mga φ - R
+ mga φ - R  =
=  Rk.
Rk.
Введем обозначения  = w
= w  ;
;  = B;
= B;  = C, и учтем, что
= C, и учтем, что
ε = 
Тогда уравнение колебаний примет вид:
 +ω
+ω 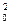 φ - B = Cwм
φ - B = Cwм
Введем новую переменную:
y = φ -  . Найдем φ =
. Найдем φ =  ,
,  =
=  ,
,  =
=  .
.
Тогда уравнение колебаний примет вид:
 + ω
+ ω  у = Сwм (172)
у = Сwм (172)
Уравнение (172) описывает вынужденные колебания в условиях резонанса. Так как колебания угловой скорости wм маятника происходят с частотой колебаний системы w, а затухание отсутствует, то в соответствии с теорией колебаний в этом случае амплитуда колебаний стремится к бесконечности.
Амплитуда вынужденных колебаний:
А =  .
.
Так как частота w = w0, то А =  . Это означает, что энергия вращения вала передается маятнику.
. Это означает, что энергия вращения вала передается маятнику.
Дадим общую теорию маятника Фруда. В общем виде уравнение колебаний маятника на втулке имеет вид:
Jφ² +μφ¢ + Dφ = f(u - φ¢). (173)
Здесь Dφ – момент возвращающей силы (силы тяжести), μφ¢ - момент сил сопротивления (трения), f(u - φ¢) – момент внешних сил, зависящий от относительной угловой скорости (т.е. угловой скорости вала u и угловой скорости колебательного движения маятника).
Функцию f(u - φ¢) можно разложить в ряд вблизи точки u, т.к. величина φ¢ мала в сравнении с u (вал вращается гораздо быстрее, чем колеблется маятник):
f(u - φ¢) = f(u) + f ¢ (u) φ¢. (174)
Здесь f(u) постоянная величина, как и f ¢ (u). Тогда имеем
Jφ² +(μ + f ¢ (u)) φ¢ + Dφ = f(u).
Это дифференциальное уравнение колебаний около смещенного положения равновесия. Характер колебаний существенно зависит от знака выражения μ + f ¢ (u). Если эта величина положительна, то мы имеем обычные затухающие колебания:
φ (t) = (f(u)/D) + A exp (-0,5(μ + f ¢ (u)) t) cos (ωt +ψ). (175)
Если μ + f ¢ (u) < 0, что возможно при f ¢ (u) < 0, то колебания маятника будут неограниченно нарастать. Реально они прекратятся, когда вал «захватит» муфту и груз начнет совершать круговые движения вокруг оси. Однако, это не колебательное движение. Наконец, может статься, что μ + f ¢ (u) = 0, тогда маятник будет совершать обычные гармонические колебания около смещенного положения равновесия.
Точно такое же уравнение как (173) можно получить, анализируя электрическую цепь на рис.49 или движения крыла самолета на рис. 50.
Рассмотрим электрический колебательный контур. Применим правила Кирхгофа к колебательному контуру на рис.49 (см. обозначения на схемем. рис.49жения крыла самолета на рис. авновесия и атических наук профессор В.К.Гончаров). Имеем:
i = Q¢(t) = I – ia; IR = - L I¢(t) – Q/C. (176)
Штрихи обозначают дифференцирование по времени. Продифференцируем второе выражение по времени еще раз и учтем первое равенство: L I²(t) + R I¢(t) + (I/C) = (ia/C), или в стандартных обозначениях
I²(t) + 2β I¢(t) + ω20I = ω20 ia, (177)
где ω20 = 1/LC; 2β = R/L.
Однако анодный ток ia есть функция напряжения на сетке триода и анодного напряжения, причем напряжение на сетке влияет значительно сильнее на него, чем анодное напряжение (что учитывается постоянным коэффициентом D << 1), т.е.
ia = f (eg0 – M I¢(t) + D(ea0 – L I¢(t)). (178)
Теперь
I²(t) + 2β I¢(t) + ω20I = ω20 f (eg0 – M I¢(t) + D(ea0 – L I¢(t)).
Разлагаем функцию f в ряд вблизи точки eg0 + Dea0, учитывая, что I¢(t) мало. Получаем
I²(t) + 2β I¢(t) + ω20I =
= ω20 f(eg0 + Dea0) - ω20 f ¢(eg0 + Dea0)(M + DL) I¢(t). (179)
Введем величину S = f ¢ (eg0 + Dea0), ее называют крутизной характеристики триода в рабочей точке. Дифференциальное уравнение имеет точно такой же вид, как и для маятника Фруда. Характер его решений определяется знаком выражения 2β + ω20 S(M + DL).
Аналогичный анализ можно провести и для изгибно-крутильного флаттера крыла (рис. 50). Если по какой-либо причине крыло прогнулось, например, вниз, то момент силы упругости конструкции крыла, приложенной в центре жесткости его конструкции, будет стремиться возвратить его в начальное положение. При этом момент инерционных сил (сил тяжести), действующих на крыло и приложенных в центре тяжести, будут поворачивать крыло вокруг центра жесткости. Если центр тяжести крыла расположен позади его центра жесткости, то крыло закрутится так, что оно увеличит свой угол атаки, возникнет дополнительный момент аэродинамических сил, приложенных в центре давления крыла. Этот момент аэродинамических сил будет стремиться продолжить изгибное движение крыла вверх. Крыло пройдет свое начальное положение, а угол атаки его при этом станет максимальным. Под действием момента аэродинамических силы крыло будет продолжать прогибаться вверх. При этом возникнет момент сил упругости, стремящийся замедлить движение крыла вверх, и момент инерционных сил, стремящийся уменьшить закручивание крыла вокруг центра жесткости. Крыло остановится в крайнем верхнем положении. Момент сил упругости, стремящийся возвратить крыло в начальное положение, станет максимальным, а момент сил инерции, имеющий в этом положении тоже наибольшую величину, будет стремиться повернуть крыло и сделать угол атаки отрицательным. Крыло начнет опускаться и закручиваться. Возникнет дополнительный момент аэродинамических сил, ускоряющий движение крыла вниз. Оно пройдет нейтральное положение, начнет уменьшать под действием момента инерционных сил свой отрицательный угол атаки и под действием момента упругих сил остановится в нижнем положении. Потом эта картина повторится.
Не нашли, что искали? Воспользуйтесь поиском: