
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
ВЫСШАЯ МАТЕМАТИКА
Часть 2
методические указания и контрольные
задания для студентов заочной и дистанционной форм обучения
Псков
УДК 51 Рекомендовано Научно-методическим
ББК 22 советом ППИ СПбГПУ
Богданова В.М., Лисенков А.В., Хватцев А.А.
Высшая математика. Часть 2: Методические указания и контрольные
задания для студентов заочной и дистанционной форм обучения. – Псков, ППИ СПбГПУ, 2004. – 23 стр.
Библиография: 4
Вторая часть учебного пособия по высшей математике охватывает приложение дифференциального исчисления функции одного аргумента к исследованию и построению графиков функций, нахождение наибольших и наименьших значений функций нескольких аргументов и интегральное исчисление функции одного аргумента. В пособии приведены рабочая программа указанных разделов, список основной и дополнительной литературы, вопросы для самоконтроля.
Учебное пособие адресовано студентам технических вузов, обучающимся по заочной и дистанционной формам обучения.
Рецензенты: доктор технических наук, академик МАН ВШ Дегтярев В.Г.,
кандидат педагогических наук Соловьева И.О.
© ППИ СПбГПУ, 2004.
Раздел 1.
ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
1. Условия возрастания и убывания функций.
2. Точки экстремума. Необходимые условия экстремума.
3. Отыскание наибольшего и наименьшего значения функции на отрезке.
4. Исследование функций на выпуклость и вогнутость. Точки перегиба.
5. Асимптоты кривых.
6. Общая схема построения графиков функций.
Литература  , гл. V, §2-6; §9-12, упр. 1,2,8,11,14,19, 32-34,62,63,72,75,76,83,84.
, гл. V, §2-6; §9-12, упр. 1,2,8,11,14,19, 32-34,62,63,72,75,76,83,84.
7. Функции нескольких переменных. Основные понятия (область определения, предел функции, непрерывность)
8. Частные производные, Полный дифференциал. Вычисление приближенного значения функции с помощью дифференциала. Касательная плоскость и нормаль к поверхности.
9. Экстремумы функции нескольких переменных.
Литература  , гл. VIII, §1,2,3,5,6,7,8,10,11,12,16,17,19.
, гл. VIII, §1,2,3,5,6,7,8,10,11,12,16,17,19.
10. Уравнение кривой в пространстве.
11. Уравнение касательной к кривой. Уравнение нормальной плоскости.
12. Кривизна кривой.
Литература  , гл. IX, §1-4, упр. 1,2,4,5,13
, гл. IX, §1-4, упр. 1,2,4,5,13
Вопросы для самопроверки.
1. Дайте определение возрастающей (убывающей) функции на промежутке.
2. Что называют интервалами монотонности функции?
3. Какие углы образуют касательные к графику возрастающей (убывающей) функции с положительным направлением оси абсцисс?
4. Приведите примеры возрастающих и убывающих функций и укажите их интервалы возрастания и убывания.
5. Сформулируйте правило нахождения интервалов монотонности функции.
6. Покажите, что функции  и
и  возрастают в любом промежутке.
возрастают в любом промежутке.
7. Дайте определение максимума (минимума) функции.
8. Какие точки называют точками экстремума функции?
9. Сформулируйте необходимое условие экстремума функции. Является ли оно достаточным условием?
10. Какие точки называются критическими точками функции?
11. Сформулируйте правило (последовательность ваших действий) нахождения экстремума функции.
12. Дайте определение наибольшего (наименьшего) значения функции на отрезке.
13. Всегда ли существуют у функции на отрезке наибольшее и наименьшее значения?
14. Сформулируйте правило нахождения наибольшего и наименьшего значения функции, дифференцируемой на отрезке.
15. Если функция непрерывна на промежутке, который не является отрезком, обязана ли она иметь на этом промежутке наибольшее и наименьшее значение?
16. Какую кривую называют выпуклой (вогнутой) на интервале?
17. Сформулируйте достаточный признак выпуклости (вогнутости) кривой на интервале.
18. Какую точку называют точкой перегиба? Что происходит со второй производной в точке перегиба?
19. Сформулируйте достаточный признак точки перегиба.
20. Сформулируйте определение асимптоты кривой.
21. В точках разрыва какого рода ищут вертикальные асимптоты?
22. Как находятся наклонные и горизонтальные асимптоты?
23. Изложите схему общего исследования функции и построения ее графика.
24. Когда функция 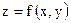 называется дифференцируемой в данной точке
называется дифференцируемой в данной точке  . Что называется полным дифференциалом этой функции в данной точке? В чем состоит правило применения полного дифференциала для вычисления приближенного значения функции, близкого к известному?
. Что называется полным дифференциалом этой функции в данной точке? В чем состоит правило применения полного дифференциала для вычисления приближенного значения функции, близкого к известному?
25. Выведите уравнения касательной плоскости и нормали к поверхности в точке М. Выясните геометрический смысл полного дифференциала функции двух переменных.
26. Дайте определение частных производных высших порядков. Сформулируйте теорему о равенстве смешанных частных производных функции двух переменных.
27. Что называется производной функции 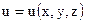 в данной точке Мо по направлению вектора
в данной точке Мо по направлению вектора  ? Выведите формулу ее вычисления.
? Выведите формулу ее вычисления.
28. Что называется градиентом скалярного поля 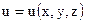 в данной точке? Как выражается производная по направлению через градиент и единичный вектор?
в данной точке? Как выражается производная по направлению через градиент и единичный вектор?
29. Дайте определение локального максимума (минимума) функции двух переменных. Выведите необходимое условие и сформулируйте достаточное условие экстремума функции двух переменных.
30. Сформулируйте правило нахождения экстремумов функции двух переменных.
31. Выведите правило нахождения наибольшего и наименьшего значения функции двух переменных в замкнутой области.
32. Что называется условным экстремумом функции 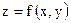 ? Как найти условный экстремум функции двух переменных, если эти переменные связаны одним условием?
? Как найти условный экстремум функции двух переменных, если эти переменные связаны одним условием?
33. Напишите уравнения касательной и нормальной плоскости к кривой.
34. Как вычислить кривизну кривой в данной точке?
Пример 1. Провести полное исследование и построить график функции
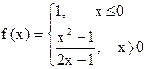
1) Найдем область определения. Функция f(x) является частным случаем «склеенной» функции, т.е. функции вида
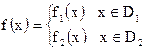 .
.
Иногда множества D1 и D2 полностью не указываются. Надо учитывать естественные области определения функций f1(x) и f2(x). В нашем примере f1(x)=1, D1=  , f2(x)=
, f2(x)=  и D2:
и D2:  .
.
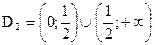
Итак, область определения функции f(x): 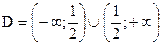 . Причем значение х=0 - точка «склеивания».
. Причем значение х=0 - точка «склеивания».
В дальнейшем каждую из функций f1(x) и f2(x) исследуем соответственно в областях D1 и D2, и поведение каждой из функций в окрестности точки «склеивания».
Так как f1(x)=1 - const, график функции на области D1 можно построить без дополнительных исследований.
Исследование функции f2(x).
а) Корни f2(x)=0 

х =1, х = -1; 
б) Промежутки знакопостоянства f2(x):

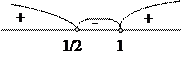
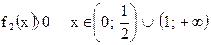
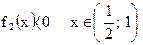
в) Поведение f2(x) в граничных точках области определения:




Прямая  является вертикальной асимптотой.
является вертикальной асимптотой.
Наклонная асимптота:



Прямая  является наклонной асимптотой на
является наклонной асимптотой на  .
.
г) Для отыскания интервалов возрастания и убывания функции найдем первую производную
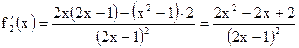
Критических точек нет, так как  . Интервалы знакопостоянства
. Интервалы знакопостоянства  :
:
 |
 + +
+ +



0 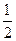
 возрастает на промежутках
возрастает на промежутках  и
и  .
.
д) Для отыскания областей выпуклости и вогнутости найдем вторую производную
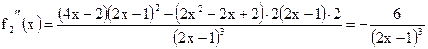
Критических точек нет. Интервалы знакопостоянства 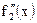 :
:
 |
 + -
+ -



0 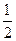
График функции  вогнут на промежутке
вогнут на промежутке  .
.
График является выпуклым на промежутке  .
.
е) Исследуем теперь функцию f(x) в окрестности точки «склеивания» х = 0



Функция f(x) непрерывна в точке х = 0.
Построим график функции:
 |
Пример 2. Найти наибольшее и наименьшее значение функции

в замкнутой области, заданной системой неравенств
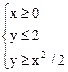
При отыскании наибольшего и наименьшего значения функции нескольких переменных в замкнутой области следует помнить, что точки, в которых достигается наибольшее и наименьшее значение, могут находиться: 1) внутри области; 2) на границах области; 3) в точках пересечения границ области.
1. Найдем точки, подозреваемые на экстремум.

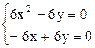
Решив систему, получим две точки 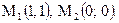 . Точка
. Точка 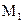 принадлежит области. Точка
принадлежит области. Точка  - лежит на границе (точка А). Обе точки принадлежат области. Значение функции в этих точках.
- лежит на границе (точка А). Обе точки принадлежат области. Значение функции в этих точках.

2. Исследуем границы области.
а) (АВ) имеет уравнение х = 0. На этой границе функция примет вид  (зависит от одной переменной). Найдем точки, подозреваемые на экстремум, это точки, в которых
(зависит от одной переменной). Найдем точки, подозреваемые на экстремум, это точки, в которых  или
или  не существует
не существует 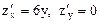 при
при  . Получили точку
. Получили точку  . Значение
. Значение  - уже вычислили.
- уже вычислили.
б) Участок (ВС) имеет уравнение у = 0.


z зависит от одной переменной х, ее наибольшее и наименьшее значения находятся среди значений в критических точках.
 при
при 
 не принадлежит участку (ВС). Найдем значение функции только в тех точках границы, которые принадлежат участку (ВС)
не принадлежит участку (ВС). Найдем значение функции только в тех точках границы, которые принадлежат участку (ВС)

в) Участок границы (АС) имеет уравнение  . На этом участке
. На этом участке
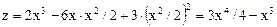

 .
.
Решая уравнение  , т.е.
, т.е.  , находим критические точки
, находим критические точки  . Точки
. Точки  принадлежат участку границы (АС).
принадлежат участку границы (АС).
 .
.
3. Находим значение функции в точках пересечения границ:

4. Наибольшее и наименьшее значение достигается в одной из найденных в процессе решения точек:  . Сравнивая значения во всех этих точках, замечаем, что самое большое из них рано 12, а самое малое -1.
. Сравнивая значения во всех этих точках, замечаем, что самое большое из них рано 12, а самое малое -1.
Ответ: 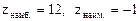 .
.
Не нашли, что искали? Воспользуйтесь поиском: