Описание установки.

Цель работы.

Проверить основное уравнение динамики вращательного движения для тела с закрепленной осью вращения. Определить
момент инерции маятника.

Оборудование.

1. Маятник Обербека.

Темы для изучения.

В лабораторной работе рассмотрены основные физические понятия кинематики и динамики вращательного движения. Получен основной закон динамики вращательного движения, проверка которого осуществля­ется на данной установке. Получена рабочая формула для определения момента инерции маятника, сделано описание установки, предложена методика проведения работы и обработки результатов измерений.

Лабораторная работа предназначена для студентов, выполняющих общий физический практикум в лаборатории механики.

Краткая теория.

Наша задача - рассмотреть вращение абсолютно твердого тела относительно неподвижной оси.

Под абсолютно твердым телом будем понимать такое тело, которое ни при каких условиях не может деформироваться, т.е. взаимное расположение и расстояние между материальными точками этого тела всегда неизменно. Здесь под материальными точками понимают не ато­мы или молекулы, а достаточно малые макроскопические объекту, на которые можно мысленно разделить твердое тело, рассматриваемое как сплошное. Массу таких материальных точек будем обозначать через _, где указывает номер материальной точки, а n показывает, на сколько материальных точек разбито наше тело.

При вращении твердого тела траектории всех точек тела являются концентрическими окружностями, центры которых лежат на оси вращения. Если положение оси вращения в пространстве с течением времени остается неизменным, то в этом случае говорят, что тело вращается около неподвижной оси. В этом случае плоскости всех концентрических окружностей перпендикулярны оси вращения, а

центры окружностей лежат на оси вращения. Все точки тела за любые равные промежутки времени совершают одинаковые угловые перемещения. Пусть твердое тело, вращаясь

вокруг оси 00’, совершило за время бесконечно малый поворот (рис. 1). Соответствующий угол поворота будем характеризовать вектором 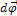, модуль которого равен углу поворота, а направление совпадает с осью ОО’, причем так, что направление поворота и направление вектора 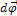связаны по правилу правого винта: направление 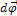вдоль оси должно быть таким, чтобы глядя вдоль него (от начала к концу), мы видели поворот совершающимся по часовой стрелке.

Выделим в твердом теле некоторую точку А, положение которой зададим радиус-вектором 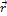проведенным из любой точки О, лежащей на оси вращения. Тогда линейное перемещение 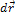конца радиус-вектора связано с углом поворота соотношением:

или в векторном виде:

(1)

Это равенство справедливо лишь для бесконечно мало­го поворота , в пре­делах которого радиус-век­тор 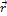можно считать не­изменным.

Вектор угловой скорости определяют как , (2)

где - промежуток времени, за который тело совершает поворот . Вектор совпадает с вектором 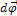. При вращении тела около неподвижной оси вектор угловой скорости имеет неизменное направление. Однако при повороте оси вращения в пространстве и при изменении скорости вращения вектор изменяется как по величине, так и по

ЛАБОРАТОРНАЯ РАБОТА. ПРОВЕРКА ОСНОВНОГО ЗАКОНА ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА КРЕСТООБРАЗНОМ МАЯТНИКЕ ОБЕРБЕКА

направлению. Изменение вектора угловой скорости со временем характеризуют вектором углового ускорения , который

определяют как

(3)

Направление совпадает с направлением 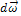- приращения вектора

Найдем скорость 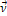произвольной точки А твердого тела, вращающегося вокруг неподвижной оси 00' с угловой скоростью .
Воспользуемся формулой (1), поделив ее на соответствующий промежуток времени . Так как и , то

(4), то (4)

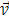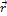т.е. скорость любой точки А твердого тела, вращающегося вокруг некоторой оси с угловой скорость , равна векторному произведению на радиус-вектор точки А относительно произвольной точки О оси вращения (рис.2).

Рис. 2

Ускорение или

(5)

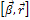В данном случае (ось вращения неподвижна) , поэтому вектор представляет тан­генциальное ускорение . Вектор же - это нормальное ускорение . Модули этих ускорений равны:

,

Отсюда модуль полного ускорения:

Основной закон динамики вращательного движения связан с понятием момента импульса и момента силы . При этом следует различать моменты этих векторов относительно точки или полюса и относительно оси. Начнем с рассмотрения моментов относительно точки.

Рис.3

Пусть 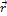- радиус-вектор, характеризующий положение материальной точки А относительно некоторой точки О, а 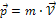ее импульс. Вектор

(6)

называется моментом импульса материальной точки. А относительно точки О. Модуль

, где плечо вектора относительно точки О (рис. 3), т.е. кратчай­шее расстояние от точки приложения до оси вращения, проходящей через О.

Продифференцируем (6) по времени t считая, что 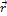и зависят от времени.

(7)

т.к. точка О неподвижна, то совпадает по направлению с , поэтому Согласно второму закону Ньютона

, где - равнодействующая сил, прило­женных к материальной точ­ке m. Тогда (7) примет вид:

(8)

где - момент силы относительно точки О (рис.4). Модуль численно равен площади заштрихованного

ЛАБОРАТОРНАЯ РАБОТА. ПРОВЕРКА ОСНОВНОГО ЗАКОНА ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА КРЕСТООБРАЗНОМ МАЯТНИКЕ ОБЕРБЕКА

параллелограмма OAFD, a является плечом относительно O. Уравнение (8) называется уравнением моментов. Оно утверждает, что производная по времени от момента импульса относительно некоторой точки O выбранной системы отсчета равна моменту равнодействующей силы относительно той же точки.

,

Уравнение моментов (8) можно обобщить на случай системы материальных точек. Моментом импульса системы материальных

точек относительно некоторого начала называется векторная сумма моментов импульсов всех материальных точек системы относительно этого же качала. Аналогично момент всех сил, действующих на систему материальных точек, определяется как векторная сумма моментов отдельных сил. Согласно (9) можно сначала найти равнодействующую этих сил, а затем вычислить ее момент. Однако внутренние силы, действующие между материальными точками согласно третьему закону Ньютона, всегда равны и противоположны: силе , с которой k - материальная точка действует на i -точку, всегда соответствует , с которой i -точка действует на k -точку. Эти две силы направлены вдоль одной прямой в противоположные стороны. Точки их приложения можно перенести в одну точку, тогда силы взаимно уничтожатся, а их полный момент будет равен 0. Тогда (8 ) примет вид:

(10)

т.е. производная по времени от момента импульса системы материальных точек относительно произвольного неподвижного начала равна векторной сумме моментов всех внешних сил относительно того же начала.

Возьмем в некоторой системе отсчета произвольную неподвижную ось Z и точку О, лежащую на этой оси. Тогда, по определению, момент импульса материальной точки относительно полюса О равен (рис. 6).

Моментом импульса относительно оси Z называют составляющую вектора параллельную оси. Можно показать, что момент силы относительно оси может быть определен как произведение перпендикулярной к оси составляющей силы на ее плечо. Обозначим момент силы, направленный по оси

ЛАБОРАТОРНАЯ РАБОТА. ПРОВЕРКА ОСНОВНОГО ЗАКОНА ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА КРЕСТООБРАЗНОМ МАЯТНИКЕ ОБЕРБЕКА

, а векторы и разложим на составляющие вдоль и перпендикулярно к оси:

;

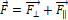Найдем :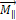

(11)

Последний член как векторное произведение параллельных векторов равен нулю. Сумма векторов в фигурных скобках представляет вектор перпендикулярный оси, поэтому его составляющая вдоль оси равна нулю. Таким образом, составляющая вектора параллельная оси

(12)

Из рис. 7 видно, что 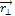- кратчайшее расстояние между осью, проходящей через точку O перпендикулярно плоскости чертежа, и линией действия , т.е. является плечом силы .

Рассмотрим вращение материальной точки массой m вокруг закрепленной оси. Тогда радиус-вектор остается постоянным по величине, кроме того, всегда , , .

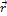
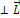В этом случае

(т.к. )

и уравнение моментов (8) примет вид:

(13)

Произведение называют моментом инерции материальной точки относительно оси вращения:

Уравнение (13) записано в скалярной форме, но ему можно придать векторную форму. Так как ось вращения неподвижна, вектор угловой скорости направлен по оси и изменяется только по величине.

Угловое ускорение направлено тоже по оси вращения. По оси вращения направлен и вектор момента, силы, поэтому уравнение моментов можно написать в виде:

(13*)

Вектор момента импульса, в случае неподвижной оси вращения, также совпадает с направлением оси:

(14)

Если вокруг оси вращается система материальных точек с одинаковой угловой скоростью , то, просуммировав моменты импульса и моменты инерции по всем материальным точкам, найдем результирующий момент импульса и суммарный момент инерции системы материальных точек относительно данной оси вращения:

,

Тогда уравнения (13) и (14) примут вид:

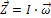(15)

(16)

где - результирующий момент всех внешних сил (суммарный момент всех внутренних сил равен нулю).

Уравнение (16) и есть основное уравнение динамики вращательного движения вокруг неподвижной оси. Оно напоминает уравнение Ньютона для движения материальной точки. В нем роль массы играет момент инерции I, роль силы - момент силы , скорости - угловая скорость , Вращение твердого тела вокруг неподвижной оси представляет вращение системы материальных точек, в которой все точки вращаются с одинаковой угловой скоростью , момент инерции I при вращении остается постоянным и уравнение (16) переходит в

(17)

Это основное уравнение вращательного движения твердого тела около неподвижной оси.

Момент инерции тела зависит от распределения массы относительно оси вращения. Тела одинаковой массы, но разной формы при вращении относительно оси, проходящей через, их центр масс, имеют разные моменты инерции. Момент инерции твердого однородного тела произвольной формы относительно некоторой оси находится по формуле:

, (18)

где - плотность тела, а интегрирование ведется по всему объему тела.

В математическом отношении нахождение момента инерции кропот­ливая задача. Она облегчается в некоторых случаях, когда тело од­нородно, имеет симметричную

ЛАБОРАТОРНАЯ РАБОТА. ПРОВЕРКА ОСНОВНОГО ЗАКОНА ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА КРЕСТООБРАЗНОМ МАЯТНИКЕ ОБЕРБЕКА

форму, а ось вращения является осью симметрии. В этих случаях можно пользоваться теоремой Штейнера: момент инерции I относительно произвольной оси Z равен сумме двух слагаемых: моменту инерции относительно оси , параллельной данной и проходящей через центр масс тела, плюс произведение массы m тела на квадрат расстояния между осями.

(19)

Моменты инерции некоторых однородных твердых тел относительно оси , проходящей через центр масс тела, приведены в следующей таблице (m - масса тела):

Твердое тело	Ось	Момент инерции
Тонкий стержень длины l	Перпендикулярна стержню и проходит через его центр	1/12
Сплошной цилиндр радиуса R	Совпадает с осью цилиндра	1/2
Тонкий диск радиуса R	Совпадает с диаметром диска	1/4
Шар радиуса R	Проходит через центр шара	2/5

Таким образом, если известны , то нахождение I осуществляется легко по (19). Например, I тонкого стержня массы m и длины l относительно оси, перпендикулярной стержню и проходящей через его конец, равен:

Вывод рабочей формулы.

Роль момента инерции при вращении твердого тела около закрепленной оси можно изучить в данной работе на крестообразном маятнике Обербека. В этой работе делается проверка основного закона вращательного движения твердого тела с закрепленной осью (17). Учитывая, что векторы , направлены по оси вращения, его можно записать в скалярной форме:

Маятник Обербека представляет собой инерционное колесо в виде крестовины. На четырех взаимно перпендикулярных стержнях

могут перемещаться грузы. На горизонтальной оси вращения О крестовины имеется двухступенчатый диск, на который наматывается нить. Один конец нити прикреплен к диску, а на втором конце подвешен груз массы m (рис. 8).

Под действием падающего груза m нить разматывается с диска и вызывает равноускоренное вращение крестовины.

Запишем уравнение движения для крестовины с грузами и поступательно движущегося груза m с учетом знаков:

(20), (21)

здесь(20)

I - момент инерции крестовины вместе с грузами;

T - величина силы натяжения нити;

- величина углового ускорения крестовину;

a - величина ускорения поступательного равноускоренного движения груза.

Для решения системы (20), (21) запишем также кинематические уравнения. Величину ускорения a можно определить, зная путь h и время t, за которое он пройден телом m:

, откуда

С другой стороны, а = βr, где r - радиус шкива. Подставив в (20) T из (21) и , получим:

(22)

Такой вид имеет основное уравнение динамики вращательного движения для нашей задачи. Однако в этом, уравнении не учтены силы трения» момент которых , очевидно, будет направлен против момента силы натяжения нити Т. Учтя это, получим:

ЛАБОРАТОРНАЯ РАБОТА. ПРОВЕРКА ОСНОВНОГО ЗАКОНА ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА КРЕСТООБРАЗНОМ МАЯТНИКЕ ОБЕРБЕКА

(23)

Момент сил трения можно оценить экспериментально и графически, если считать его постоянным. Об этом будет сказано ниже.

Описание установки.

На вертикальной колонне (1), установленной на основании (2), прикреплены два кронштейна: нижний неподвижный (З), верхний подвижный (4) и две неподвижные втулки: нижняя (5) и верхняя (6).

Основание снабжено регулируемыми ножками (7), обеспечивающими горизонтальную установку прибора. На верхней втулке (6) посредством основания (8) закреплен подшипниковый узел (9) и сам диск (10).

Через диск (10) перекинута нить (II), один конец которой прикреплен к двухступенчатому диску (12), а на другом закрепляются грузы (13).

На нижней втулке (5) посредством основания (14) прикреплен тормозной электромагнит (15), который после подключения к нему напряжения питания удерживает с помощью фрикционной муфты

ЛАБОРАТОРНАЯ РАБОТА. ПРОВЕРКА ОСНОВНОГО ЗАКОНА ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА КРЕСТООБРАЗНОМ МАЯТНИКЕ ОБЕРБЕКА

систему (крестовину вместе с грузами) в состоянии покоя.

Подвижный кронштейн (4) можно перемещать вдоль колонны и фиксировать его в любом положении, определяя, таким образом, длину пути груза. С этой целью на колонне нанесена миллиметровая шкала (16).

На подвижном кронштейне (4) закреплен верхний фотоэлектрический датчик (17). На подвижном кронштейне (3) закреплен нижний фотоэлектрический датчик (18), фиксирующий конец измерения времени и включающий тормозной электромагнит (15).

К кронштейну (3) прикреплен кронштейн (19) с резиновым амортизатором, на который опускается движущийся груз в конце пути.

На основании прибора жестко крепится ииллисекундомер FPM-15. К гнездам ZL1 и ZL2 миллисекундомера подключены соответственно фотоэлектрические датчики (17) и (18). Эти гнезда расположены на задней панели миллисекундомера. Там же расположена заземляющая клемма ZL3.

Не нашли, что искали? Воспользуйтесь поиском: