ОСНОВЫ ТЕОРИИ ЦИКЛОВ

Прирола данных

Любой ряд данных может быть разбит на три компонента: (1) силы ро­ста, (2) периодические силы и (3) случайные силы (рис. 16.4). Цикли­ческий анализ занимается поиском периодических или повторяющихся моделей в данных*.

Силы роста заставляют временные ряды медленно расти или снижать­ся с течением времени и фактически являются синонимом тенденции, или тренда. Случайные силы — это факторы, которые вызывают нере­гулярные колебания в данных, они по определению непредсказуемы. Циклический аналитик, обнаружив тренд, вычитает его из данных, что­бы удалить влияние сил роста, и сглаживает данные, чтобы удалить слу­чайные колебания, и, таким образом, находит периодические модели.

Циклическая модель

В начале XX века циклические аналитики стали пользоваться матема­тическим аппаратом для определения циклов. Цикл стали описывать как синусоидальную волну, используя при этом язык физики и статистики. С тех пор говорят, что у цикла есть частота, амплитуда и фаза, так же, как и у электромагнитных волн. Поскольку эта терминология универ­сально используется для описания циклов, важно ее определить.

Слово «цикл» происходит от греческого слова, означающего круг, которое в своем наиболее обшем смысле просто указывает на законченную последо­вательность событий, без подразумевания какой-либо регулярности во времен­ных интервалах. Циклический аналитик, тем не менее, озабочен периодичес­кими событиями, т. е. теми циклами, в которых наблюдается регулярность вре­менных интервалов.

ГЛАВА 16. анализ циклов фьючерсных рынков 577

Рисунок 16.4. ОСНОВНЫЕ КОМПОНЕНТЫ ДАННЫХ

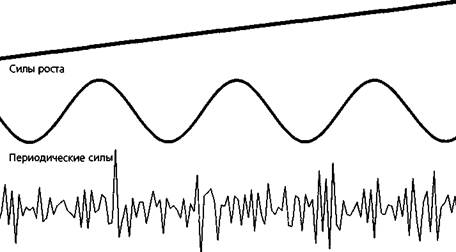
Случайные силы

Период и частота

Длина цикла — временной отрезок от одного гребня до другого или от одной впадины до другой — называется его периодом (рис. 16.5). Частота — это количество циклов внутри определенного отрезка дан­ных, она обратно пропорциональна периоду:

частота = длина отрезка данных/период.

Например, для серии данных из 200 точек цикл с периодом 20 имел бы частоту 10 (10 = 200/20). Существует два основных математичес­ких метода анализа циклов — гармонический анализ и спектральный анализ. Первый из них основан,на периоде, а второй — на частоте.

Не нашли, что искали? Воспользуйтесь поиском: