Задание 2. Гирлянда (10 баллов).

Классы (1 тур)

Задание 1. Перебор вариантов (по 10 баллов – всего 20 баллов)

1. Слово «симметрия» пришло из Древней Греции и означает оно гармонию, красоту и пропорциональность в объекте. Зеркально симметричным считается объект, состоящий из двух половин, которые являются зеркальными двойниками по отношению друг к другу относительно некоторой прямой, называемой осью симметрии. Рассмотрим квадрат размера 3х3 (рисунок 1), эта фигура имеет несколько осей симметрии, в том числе диагональ квадрата. Закрасим несколько клеток квадрата, при этом может опять получиться симметричная относительно диагонали фигура (как на рисунках 2 и 3) или несимметричная (как на рисунке 4).

Рис. 1

Рис. 2

Рис. 3

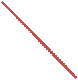Рис. 4

Нарисуйте все возможные симметричные относительно диагонали квадраты размера 3х3, содержащие ровно 3 закрашенные клетки. Посчитайте их количество.

2. Жили-были четыре фигуры: синяя звездочка, зеленый треугольник, красный квадрат и желтый круг. Распределите фигуры по своим домикам, если известно, что в первом доме живет НЕ звездочка, во втором доме НЕ зеленая фигура, в третьем доме живет НЕ квадрат, а в четвертом доме живет НЕ желтая фигура. Причем квадрат и треугольник являются соседями снежинки, то есть живут рядом со снежинкой.

Задание 2. Гирлянда (10 баллов).

Для украшения комнаты Ваня купил красивую гирлянду, представляющую собой сеть из звеньев с разноцветными лампочками разной длины. Ваня разложил гирлянду на полу и измерил длины всех звеньев (в сантиметрах), на рисунке изображено, что у него получилось (слева и справа находятся крепления гирлянды):

Чтобы решить, на какую стену вешать гирлянду, Ване нужно узнать ее длину, то есть на каком максимальном расстоянии друг от друга Ваня сможет разместить крепления гирлянды.

З адание 3. Деление клеток (10 баллов)

В некоторой лаборатории ученые занимаются изучением процесса размножения клеток. Каждую секунду каждая клетка делится на две, причем все полученные клетки нумеруются определенным образом. В начальный момент времени есть только одна клетка с номером 0, после ее деления образуются 2 клетки: назовем их старшая (С) и младшая(М), им присваиваются номера 1 и 2. Далее клетка с номером 1 делится на две: старшую с номером 3 и младшую с номером 4, а клетка с номером 2 делится на две: старшую с номером 5 и младшую с номером 6. Через 3 секунды у ученых уже 8 клеток с номерами с седьмой по четырнадцатую (процесс деления изображен на рисунке):

Теперь ученых интересует вопрос, через сколько секунд и путем деления каких клеток (старших или младших) получена клетка с определенным номером? Например, для получения клетки с номером 11 понадобилось 3 секунды, причем нужно было взять сначала младшую клетку (М), затем старшую(С) и затем еще раз старшую(С), обозначим эту последовательность МСС. А для получения клетки с номером 15 понадобится 4 секунды и последовательность клеток будет СССС.

Определите, через сколько секунд получится клетка с номером 100, и с помощью какой последовательности старших (С), младших (М) клеток она будет получена.

Не нашли, что искали? Воспользуйтесь поиском: