Вычисление премий достаточных для неразорения компании с заданной вероятностью для разных возрастных групп договоров краткосрочного страхования жизни

Пусть портфель страховой компании состоит из N договоров краткосрочного страхования жизни. Договора краткосрочного страхования жизни делятся на m групп с различным вероятностями смерти, которые зависят от возраста застрахованных:

₁ договоров для людей в возрасте от x₁ до x₂ лет, ₂ договоров для людей в возрасте от x₂ до x₃ лет, …, _m договоров в возрасте от x_m до x_m+1 лет.

Для i-ой группы людей в возрасте от x_i до x_i+1 лет вероятность смерти от естественных причин равна , а от несчастного случая 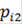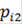_, где i принимает значения от 1 до m.

В случае смерти человека от несчастного случая страховая компания выплачивает сумму равную рублей, а в случае смерти от естественных причин сумму равную S₂ рублей.

Необходимо определить премии для всех групп договоров краткосрочного страхования сроком на 1 год, которые гарантировали бы заданную вероятность q выполнения компанией всех своих обязательств.

Найдем премии для краткосрочного страхования жизни для каждой группы договоров.

Индивидуальный убыток по каждому договору i-ой группы равен ξ_i, где ξ_i - случайная величина, которая принимает три значения:

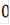
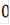с вероятностью (1- - ),

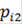
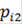с вероятностью ( ),

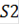
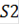с вероятностью ( ),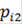

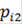где i=1,…,m.

Суммарная выплата по портфелю есть случайная величина S:

Среднее значения и дисперсии величин индивидуальных убытков есть

,

,

…

,

…

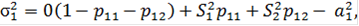
Среднее значение и дисперсия суммарных выплат по всему портфелю равны:

Предположим, что суммарная премия равна . Используя гауссовское приближение для центрированной и нормированной величины суммарных выплат, мы можем представить вероятность неразорения компании в следующем виде:

Для того, что бы вероятность неразорения была равна Q, величина 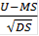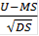должна быть равной (1-q)-процентной точке стандартного нормального распределения x_(1-Q)%, т.е. суммарная премия должна быть равна

где - суммарная нетто-премия, а - защитная надбавка, обозначим ее :

=

Пусть ₁, ₂,…, _m - защитные надбавки для договоров из каждой группы. Тогда

Рассмотрим три случая выбора защитной надбавки:

) Защитная надбавка для индивидуального договора берется пропорциональной нетто-премии;

) Защитная надбавка для индивидуального договора берется пропорциональной дисперсии выплат по договору;

) Защитная надбавка для индивидуального договора берется пропорциональной среднему квадратическому отклонению выплат по договору.

) Относительная страховая надбавка одна и та же для всех договоров и равна

а индивидуальные защитные надбавки пропорциональны нетто-премиям:

₁= ₁, ₂= ₂, …, _m= _m.

Поэтому премии для договоров из каждой группы будут равны:

.

)Еслидобавочная сумма L делится пропорционально дисперсиям, коэффициент пропорциональности

тогда для договоров из каждой группы страховые надбавки равны

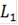
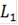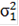
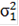= k ,

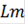
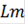= k ,

…

= k ,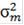

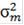а премии равны

…

3) Если добавочная сумма L делится пропорционально средним квадратическим отклонениям, коэффициент пропорциональности

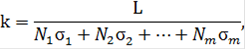
тогда для договоров из каждой группы страховые надбавки равны

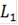
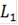= k ,

= k ,

= k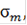

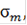
а премии равны

…

Заключение

В реферате были рассмотрены и рассчитаны основные модели расчета схем краткосрочного жизни:

- Высчитали премии группы краткосрочного страхования со страховой суммой равной S.

- Определили общие премии, достаточные, чтобы обеспечить вероятность неразорения компании, при определенном количестве застрахованных человек различных возрастных категорий.

Не нашли, что искали? Воспользуйтесь поиском: