Элементы теории вероятностей.

Случайным событием называется событие, которое при данных условиях может произойти, а может и не произойти.

Комплекс условий, которые необходимы для того, чтобы событие могло произойти (или не произойти), называется испытанием.

Исходом испытания называется появление в результате этого испытания какого-либо случайного события.

Если в результате испытания произошло интересующее нас событие, говорят о благоприятном исходе испытания. Если же это событие не произошло, исход называют неблагоприятным.

Относительная частота события А (Р^*(А)) - это отношение числа благоприятных исходов к числу испытаний, т.е.

Учитывая, что 0 £ m £ n, для относительной частоты случайного события запишем: 0 £ Р*(А) £ 1.

Статистическое определение вероятности. Вероятность случайного события – это предел, к которому стремится относительная частота этого события при неограниченном увеличении числа испытаний.

Если в результате испытания могут наблюдаться различные исходы, причем нет оснований считать, что какой-то из этих исходов может наблюдаться чаще или реже, чем другие, то такие исходы называют равновозможными.

Классическое определение вероятности. Вероятность случайного события - это отношение числа благоприятных исходов к общему числу всех равновозможных исходов, т.е.

,

где Р(А) - вероятность события А, m - число благоприятных исходов, n - число всех равновозможных исходов.

Свойства вероятности:

1. 0 £ Р(А) £ 1,

2. Событие, которое не может не произойти при испытании (т.е. m=n), называется достоверным. P(A)=1.

3. Событие, которое не может произойти при испытании (т.е. m = 0, а n ¹ 0), называется невозможным. P(A)=0

События А и В называются несовместными, если появление события А исключает возможность появления события В.

Если несовместные события А₁, А₂, А₃, …, А_n образуют такую группу событий, что в результате испытания обязательно происходит одно из этих событий и не может произойти никакое другое событие, не входящее в эту группу, то говорят, что события А₁, А_2,, А₃, …, А_n образуют полную группу событий.

События А и В являются противоположными, если из того факта, что при испытании не произошло одно из них, вытекает факт, что при этом обязательно произошло другое.

Если два несовместных события образуют полную группу событий, они являются противоположными. Событие, противоположное событию А, часто обозначают .

События А и В называются независимыми (зависимыми), если вероятность одного из них не зависит (зависит) от того, произошло или не произошло другое.

Если вероятность события В зависит от того, произошло или не произошло событие А, говорят об условной вероятности события В, для которой используется обозначение Р(В/А).

Теорема сложения вероятностей для несовместных событий. Если имеется несколько несовместных событий А₁, А₂, …, А_n, то вероятность сложного события, состоящего в том, что произойдет одно из этих событий (то есть произойдет или событие А₁, или событие А₂, … или событие А_n), равна сумме вероятностей этих событий, т.е.

Р(А₁ или А₂ … или А_n) = Р(А₁) + Р(А₂) + … + Р(А_n).

Следствия теоремы сложения вероятностей:

1. Если несовместные события А₁, А₂, …, А_n образуют полную группу событий, то

Р(А₁) + Р(А₂) + Р(А₃) + … + Р(А_n) = 1.

2. Если события А и В являются противоположными, то

Р(А) + Р(В) = 1 или Р(А) = 1 – Р(В).

Теорема умножения вероятностей для независимых событий. Если события А₁, А₂, …, А_n – независимые, то вероятность сложного события, состоящего в том, что произошли все эти события (то есть произошло и событие А₁, и событие А₂, …, и событие А_n), равна произведению вероятностей этих событий, т.е.

Р(А₁ и А₂ … и А_n) = .

Теорема умножения вероятностей для зависимых событий. Если события А₁ и А₂ - зависимые, то вероятность сложного события, состоящего в том, что произошли оба эти события (и событие А₁, и событие А₂), равна произведению вероятности одного из этих событий на условную вероятность другого, т.е.

Р(А₁ и А₂) = Р(А₁) × Р(А₂ /А₁) = Р(А₂) × Р(А₁ /А₂).

Формула Бернулли. Пусть вероятность одного из двух противоположных событий равна р, а вероятность второго равна q, причем q = 1 – p. Если в этой ситуации производится n испытаний, причем вероятность появления первого события при каждом очередном испытании не зависит от того, какое из этих двух событий появлялось в предыдущих испытаниях, то вероятность того, что первое событие при этом появится m раз (Р(m из n)), может быть вычислена по формуле Бернулли

Р(m из n)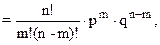

где n! = 1 × 2 × 3 ×... × n. 0! = 1.

Формулы полной вероятности и Байеса используются в ситуации, в которой событие А может появляться только одновременно с одним из несовместных событий В_i (i = 1, 2,..., n), образующих полную группу событий. Пусть вероятность события В_i равна Р(В_i), а вероятность события А при условии, что произошло событие В_i, равна Р(А/В_i). Тогда безусловная вероятность события А может быть вычислена по формуле полной вероятности:

В частном случае, когда n = 2, события В₁ и В₂ являются противоположными. Если при этом их обозначить В и 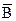, то в этом случае формула полной вероятности имеет вид:

.

Пусть теперь вероятность события Вj при условии, что событие А уже произошло, равна Р(Вj/А). Тогда эта вероятность может быть вычислена по формуле Байеса

При применении формулы Байеса вероятности Р(В_i) называют априорными, а вероятности Р(В_j/А) – апостериорными.

Пример 1. В ящике находятся шары белого, черного и красного цвета. Всего в ящике 20 шаров. Из ящика, не глядя, достают один шар. Вероятность того, что этот шар белый (Р(б)), равна 0,5, а вероятность того, что он красный (Р(к)), равна 0,2. Сколько в ящике черных шаров?

Решение

Пусть m – искомое число черных шаров, а Р(ч) – вероятность того, что вынутый шар – черный. Тогда Р(ч) . С другой стороны, события, состоящие в том, что вынутый шар является белым, черным или красным составляют полную группу несовместных событий. Поэтому

Р(б) + Р(ч) + Р(к) = 1 или Р(ч) = 1 – Р(б) – Р(к) = 1 – 0,5 - 0,2 = 0,3.

Тогда и .

Пример 2. Вероятность рождения мальчика (Р(м)) равна 0,52. В семье трое детей. Какова вероятность того, что а) в семье три мальчика; б) в семье один мальчик; в) в семье есть хотя бы одна девочка?

Решение

Рождения мальчика и девочки – это противоположные события. Поэтому вероятность рождения девочки (Р(д)) равна

Р(д) = 1 – Р(м) = 1 – 0,52 = 0,48.

а) В соответствии с теоремой умножения вероятностей для независимых событий

Р(3 м) 0,14.

б) В соответствии с теоремами сложения и умножения вероятностей

Р(1 м) = Р((м и д и д) или (д и м и д) или (д и д и м)) =

.

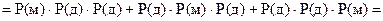
в) Событие, состоящее в том, что в семье есть хотя бы одна девочка, и событие, состоящее в том, что в семье нет ни одной девочки (т.е. в семье три мальчика), являются противоположными. Поэтому для искомой вероятности можно записать

Р(хотя бы одна девочка) = 1 – Р(3 м) = 1 – 0,14 = 0,86.

Пример 3. В ящике находятся 5 белых, 3 черных и 2 красных шара. Не глядя, из ящика вынимают два шара. Какова вероятность того, что оба шара черные, если: а) первый вынутый шар возвращается обратно в ящик до того, как будет вынут второй шар; б) первый вынутый шар обратно не возвращается?

Решение

Для решения задачи используем теорему умножения вероятностей, учитывая, что в первом случае события являются независимыми, а во втором – зависимыми.

а) Р(черный и черный) = Р(черный) × Р(черный) = = = 0,09;

б) Р(черный и черный) = Р(черный) × Р(черный /черный) = .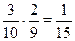

Пример 4. В условии предыдущей задачи вычислить вероятность того, что вынуты белый и черный шары.

Решение

В этом случае необходимо использовать и теорему сложения вероятностей, и теорему умножения вероятностей.

Учитывая, что возможна ситуация, когда сначала будет вынут белый, а затем черный шары, и ситуация, когда сначала будет вынут черный, а затем – белый шары, для искомой вероятности (Р) можно записать:

а) Р = Р((б и ч) или (ч и б)) = Р(б и ч) + Р(ч и б) = Р(б) × Р(ч) + Р(ч) × Р(б) =

=0,5 × 0,3 + 0,3 × 0,5 = 0,3;

б) Р = Р((б и ч) или (ч и б)) = Р(б и ч) + Р(ч и б) = Р(б) × Р(ч/б) + Р(ч) × Р(б/ч) =

= .

Пример 5. Студент знает 96 из 100 вопросов, вынесенных на экзамен. Какова вероятность того, что из трех вопросов, содержащихся в билете он: а) знает все три вопроса; б) знает один вопрос; в) знает не более двух вопросов?

Решение

Пусть событие з – студент знает вопрос, событие н - студент не знает вопрос.

а) Р(3 з) = Р(з) × Р(з /з) × Р(з /(з и з)) = ;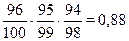

б) Р(1 з) = Р(з) × Р(н /з) × Р(н /(з и н)) + Р(н) × Р(з /н) × Р(н /(н и з)) +

+ Р(н) × Р(н/н) × Р(з/(н и н)) = ;

в) Р(з ≤ 2в) = 1 – Р(3 з) = 1 – 0,88 = 0,12.

Пример 6. Стрелок при одном выстреле попадает в цель с вероятностью 0,8. Определить вероятность семи попаданий в серии из десяти выстрелов.

Решение

Для решения используем формулу Бернулли. Здесь m = 7;

n = 10; p = 0,8; q = 0,2. Следовательно,

Р(7 из 10) =

Пример 7. Четыре завода выпускают одинаковые изделия, причем их производительности в год составляют: I завод - 500 шт., II завод - 1000 шт., III завод - 200 шт., IV завод - 1000 шт. Известно, что вероятность выпуска бракованного изделия составляет: на I заводе - 0,01, на II заводе - 0,01, на III заводе - 0,005, на IV заводе - 0,004. Определить вероятность того, что наугад выбранное из годовой продукции этих заводов изделие является бракованным.

Решение

Обозначим событие, состоящее в том, что изделие выпущено I заводом - В₁, II заводом - В₂, III заводом - В₃, IV заводом - В₄. Тогда

;

; ; .

Обозначим событие, состоящее в том, что изделие бракованное, А. По условию ; ; 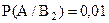; . В соответствии с формулой полной вероятности

.

Пример 8. Отделение больницы специализируется на лечении трех заболеваний, причем количества больных I, II и III заболеваниями соотносятся как 1:5:3. Известно, что некоторый комплекс симптомов встречается при I заболевании с вероятностью 0,7; при II - с вероятностью 0,3; при III - с вероятностью 0,2. Определить: а) вероятность наличия указанного комплекса симптомов у наугад выбранного пациента этого отделения; б) вероятность того, что у наугад выбранного пациента отделения имеется первое заболевание, если у него обнаружено наличие указанного комплекса симптомов.

Решение

Обозначим события, состоящие в том, что у пациента имеется I, II или III заболевание, В₁, В₂, и В₃ соответственно. Очевидно, что

; ; .

Обозначим событие, состоящее в том, что у больного есть указанный комплекс симптомов, А. Тогда Р(А /В₁) = 0,7; Р(А /В₂) = 0,3; Р(А /В₃) = 0,2.

В соответствии с формулой полной вероятности

.

После этого, в соответствии с формулой Байеса

.

Не нашли, что искали? Воспользуйтесь поиском: