Камеральные работы при обработке результатов измерений

а) Обработка журналов. Составление схемы теодолитных ходов

Камеральные работы начинают с проверки полевых журналов. Затем на бумаге по средним значениям углов и длинам линий составляют схему теодолитных ходов. На схеме показывают твердые пункты.

б) Уравнивание теодолитного хода

Уравнивание углов

Рис. 8.22. Разомкнутый ход

Рис. 8.23. Замкнутый ход

1) Подсчет суммы измеренных углов по формуле

Sb_изм = b₁ + b₂ +…. (8.12)

2) Вычисление теоретической суммы углов для разомкнутого хода по формулам

Sb_теор = (a_кон - a_н) + 180°· n (если измерены левые углы),

Sb_теор = (a_н - a_кон) + 180°· n (если измерены правые углы), (8.13)

для замкнутого хода:

Sb_теор = 180°· (n - 2) (для внутренних углов). (8.14)

3) Вычисление угловой невязки хода по формуле

f_b = Sb_изм - Sb_теор. (8.15)

4) Вычисление допустимой угловой невязки хода

f_bдоп = ± 1¢Ön. (8.16)

Если f_b £ f_bдоп, угловые измерения признаны доброкачественными.

5) Вычисление поправок в измеренные углы

. (8.17)

6) Вычисление уравненных углов b_ур

b_ур = b_изм + v_b. (8.18)

Контролем правильности вычисления поправок является выполнение условия

Sv_b = - f_b, (8.19)

а правильности их введения в углы – условие

Sb_ур = Sb_теор. (8.20)

7) Вычисление дирекционных углов всех линий хода

a₁ = a_н + 180° + - для левых углов,

a₁ = a_н + 180° - - для правых углов. (8.21)

Контролем правильности вычисления дирекционных углов является получение конечного дирекционного угла a_кон – для разомкнутого хода и a_н – для замкнутого хода.

Вычисление координат пунктов

1) Вычисление приращений координат по уравненным дирекционным углам и горизонтальным проложениям линий

Dх = d cos a,

Dу = d sin a. (8.22)

2) Вычисление суммы вычисленных приращений координат по осям х и у:

SDх _выч = Dх₁ + Dх₂ +…+Dх_n,

SDу _выч = Dу₁ + Dу₂ +…+Dу_n. (8.23)

3) Вычисление теоретической суммы приращений координат для разомкнутого хода:

SDх _теор = х_кон - х_нач,

SDу _теор = у_кон - у_нач; (8.24)

для замкнутого хода SDх _теор = 0,

SDу _теор = 0. (8.25)

4) Вычисление невязок по осям координат для разомкнутого хода

f_х = SDх _выч - SDх _теор,

f_у = SDу _выч - SDу _теор; (8.26)

для замкнутого хода f_х = SDх _выч,

f_у = SDу _выч. (8.27)

5) Вычисление абсолютной невязки хода

f_S = (8.28)

и относительной невязки хода

(8.29)

характеризующей качество полевых измерений. Должно выполняться условие:

.

6) Уравнивание хода состоит в распределении невязок f_х и f_У с их обратным знаком на все вычисленные приращения координат пропорционально длинам сторон хода. Поправки v_х и v_у вычисляют по формулам:

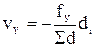, . (8.30)

7) Исправленные приращения координат получают как алгебраическую сумму вычисленных приращений и соответствующих поправок к ним, т.е.:

Dх _испр = Dх _выч + v_X,

Dу _испр = Dу _выч + v_у. (8.31)

Контролем правильности вычисления поправок является выполнение условий:

Sv_X = - f_х, Sv_у = - f_у, (8.32)

а правильности вычисления исправленных приращений координат - условий

SDх _испр = SDх _теор,

SDу _испр = SDу _теор. (8.33)

8) Вычисление координат точек хода производится по формулам:

х_n+1 = х_n + Dх _испр,

у_n+1 = у_n + Dу _испр. (8.34)

Контролем вычислений является получение координат конечного пункта, если ход разомкнутый, и координат начального пункта, если ход замкнутый.

Не нашли, что искали? Воспользуйтесь поиском: