Лабораторная работа № 2

С целью исследования закона распределения ошибки измерения концентрации кислорода газоанализатором было выполнено 315 измерений. Совокупность погрешностей представлена в виде статистического ряда (табл.№2).

Таблица №2

∆С,%		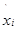ni	pi	∆С,%		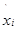ni	pi
-0,50 ÷ -0,45	-0,475		0,0381	0 – 0,05	0,025		0,05714
-0,45 ÷ -0,40	-0,425		0,06032	0,05 – 0,10	0,75		0,06032
-0,40 ÷ -0,35	-0,375		0,05397	0,10 – 0,15	0,125		0,04762
-0,35 ÷ -0,30	-0,325		0,04762	0,15 – 0,20	0,175		0,05079
-0,30 ÷ -0,25	-0,275		0,05079	0,20 – 0,25	0,225		0,04127
-0,25 ÷ -0,20	-0,225		0,04444	0,25 – 0,30	0,275		0,05397
-0,20 ÷ -0,15	-0,175		0,05714	0,30 – 0,35	0,325		0,05079
-0,15 ÷ -0,10	-0,125		0,0381	0,35 – 0,40	0,375		0,05079
-0,10 ÷ -0,05	-0,075		0,05079	0,40 – 0,45	0,425		0,04444
-0,05 ÷ -0	0,025		0,04127	0,45 – 0,50	0,475		0,06032

Производите выравнивание с помощью закона равномерной плотности и проверьте согласованность теоретического и статистического распределений с помощью критерия χ². Доверительную вероятность того, что значения χ², полученное по опытным данным, будет меньше соответствующего значения (χ*)² теоретического распределения, принять равной p=0,05. Для этой вероятности при k=17

,

при k=18

,

при k=19

,

где k-число степеней свободы.

Закон равномерной плотности определяются выражением

где .

Математическое ожидание и дисперсия подсчитываются по формулам

; .

При выравнивании следует выбрать α и β таким образом, чтобы х₀ и D были равны статистическому среднему и статистической дисперсии . В нашем случае

;

.

Следовательно, ; , откуда

α = - 0,5415 и β=0,05515.

Таким образом, .

На рис.№2 представлена гистограмма и выравнивающий её закон равномерной поверхности f(x).

Для поверки соответствия опытного распределения теоретическому используем критерий χ².

Для этого вычисляем значение критерия χ². По формуле

,

где h - число интервалов; n_i – число наблюдений в i -ом интервале; n – общее число наблюдений; - теоретическая (т.е. в соответствии с выбранным теоретическим законом распределения) вероятность попадания в i -ый интервал.

Рис. 2

Для закона равномерной плотности при одинаковой плотности при одинаковых интервалах вероятность попадания будет одинакова для всех интервалов:

Определим число степеней свободы s. Оно определяется как число интервалов минус число наложенных связей. В нашем случае число наложенных связей равно трем.

Первая – сумма частот равна единице:

,

вторая – теоретическое и статистическое (экспериментальное) среднее значения должны быть равны:

;

третья – теоретическая и статистическая дисперсия должны быть равны:

.

Следовательно, в нашем случае число степеней свободы s = 20 – 3 = 17.

Вычисляем . Так как , то гипотеза о согласовании теоретического и экспериментального распределений считается правдоподобной.

Не нашли, что искали? Воспользуйтесь поиском: