Для специальности «Строительство и эксплуатация зданий и сооружений»

Задание №5

Для расчетно-графической работы.

«Графический расчёт ферм с помощью диаграммы Максвелла-Кремоны»

Для специальности «Строительство и эксплуатация зданий и сооружений»

(Пример расчёта)

Преподаватель: Фофанова В.В.

К выполнению задания рекомендуется приступить после изучения тем:

- плоская система сходящихся сил; условия равновесия;

- статически, определимые фермы; графический и аналитический расчёт.

Задание: Определить усилия в стержнях фермы путём построения диаграммы Максвелла-Кремоны. Указать растянутые, сжатые, нулевые стержни. Выполнить проверку 2 ^х сил аналитическим способом.

1) Определяем опорные реакции фермы R_а и R_в . Т.к. нагрузка приложена симметрично относительно вертикальной оси, то реакции R_а и R_в будут равны половине нагрузки: R_а = R_в = = = 2F = 20 (кН).

2) Обозначим внешние и внутренние поля, т.е зоны между внешними и внутренними силами. При этом обходим ферму по часовой стрелке. Внешние поля обозначим: а, в, с, с́, в́, а́, d.

Внутренние поля: 1, 2, 3, 4, 4́, 3́, 2́, 1́.

Присвоим силам индексы зон между которыми они лежат, обходя ферму по часовой стрелке: aв, F_вс, F_cć, F_ćв́, в́á, R_ád(R_в), R_da (R_a) схема фермы должна быть вычерчена в масштабе (на рис. 1м – 1см).

3) Выберем масштаб сил (1см = = 5 кН). Строим вертикальную силовую линию а – в – с - с́ - в́ - а́ (в масштабе её длина 8 см). На ней приложены внешние силы: ав; F_вс ; F_cć ; F_ćв́ ; в́а́.

Разделим её пополам точкой d. Из т.d влево проведём горизонталь. Эта силовая линия, представляет собой замкнутый силовой многоугольник внешних сил и опорных реакций.

4) Приступим к построению диаграммы т.к. каждый узел фермы представляет собой плоскую систему сходящихся сил и находится в равновесии, то для каждого узла можно построить замкнутый силовой многоугольник.

Объединённые на одном чертеже замкнутые силовые многоугольники и представляют собой диаграмму Максвелла – Кремоны.

Начинаем с узла, где сходятся 2 стержня – это узел Д. В нём сходятся стержни в – 1 и 1 – а. Наименования стержня – зоны, между которыми он лежит, при обходе узла по часовой стрелке.

Узел Д. Стержни в – 1 и 1 – а – общая зона – 1. Точку 1 надо построить на диаграмме. Узел Д представляет собой частный случай 2 (см. частные случаи равновесия узлов – приложение).

N_в-1 = 0 – точки в и 1 совпадают

N_1-а = = 5(кН)

Сила N_1-a направлена от т. 1 к т. а, т.е. снизу вверх. Мысленно переносим это движение на схему фермы и видим, что сила N_1-а направлена вверх, т.е. к узлу Д (сжатие), т.е. N_1-a = - 5(кН).

Узел А. Неизвестные стержни в этом узле: 1 – 2 и 2 – d (обход узла по час. стрелке). Общая зона – 2 (точку 2 надо построить)

Из точек 1 и d проводим линии, параллельные стержням 1 – 2 и 2 – d до их пересечения в т.2.

Измеряем длины отрезков:

N_1-2 = 4,4 см * 5 = 22 (кН) (- 22 кН) – направлена к узлу А (сжатие)

N_2-d = 3,3 см * 5 = 16,5 (кН) – направлена от узла А (растяжение)/

Узел Н: Стержни 2 – 3 и 3 – d – общая зона 3:

Узел Н представляет собой частный случай 2 (см. приложение частные случаи равновесия узлов)

N_2-3 = 0 – точки 2 и 3 совпадают.

N_3-d= N_d-2(2-d) = 3,3 * 5 = 16,5 (кН) – направлена от Н(растяжение)

Узел Е: Неизвестные стержни: с – 4 и 4 – 3. Общая зона – 4. Из точек с и 3 проводим линии, параллельные стержням с – 4 и 4 – 3 до их пересечения в т.4.

N_c-4 = 3,5 см * 5 = 17,5 (кН) (- 17,5 кН) – направлена к узлу Е(сжатие).

N_4-3 = 0,2 см * 5 = 1 (кН) направлена от Е (растяжение).

Узел К: Неизвестные стержни: с ́ - 4́ ́ и 4́ ́ - 4. Общая зона – 4 ́. Из точек с ́ и 4 проводим линии, параллельные стержням с ́ - 4́ ́ и 4́ ́- 4 до их пересечения в т. 4 ́.

N_{́ с ́ - 4́ ́} = 3,5 см * 5 = 17,5 (кН)(- 17,5 кН) – направлена к узлу К(сжатие) (=N_c-4)

N_{4́ ́- 4} = 0,3 см * 5 = 1,5(кН) (- 1,5 кН) – направлена к узлу К (сжатие).

Далее строим диаграмму для правой половины фермы симметрично вниз относительно горизонтали d. Обозначаем на схеме фермы и на диаграмме растянутые, сжатые и нулевые стержни.

5) Выполним проверку 2^х сил аналитическим способом – способом моментных точек. Проверим силы N_c-4 и N_{3 – d}.

Для этого проверим сечение I – I, перерезав указанные стержни. Оставим одну часть фермы (левую), отбросив другую.

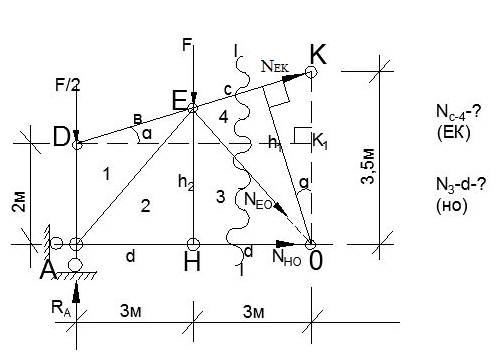
Моментная точка для определения силы N_EK – узел 0 – т. пересечения 2^х других перерезанных сил N_EO и N_HO.

Составим сумму моментов сил для оставленной части фермы относительно т.О:

∑ М₀^ост = R_А*6 - * 6 – F * 3 + N_EK * h₁ = 0

h₁ = |Ko| *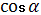

Из ∆ - ка ДКК₁: = = 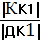= 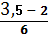0,25. = 14°.

h₁ = 3,5 * 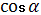= 3,5 * 0,9703 = 3,396 ≈ 3,4 (м).

N_EK = 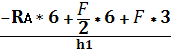= = 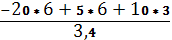- 17,6(кН) (сжатие).

Из диаграммы N_c-4 = - 17,5 (кН) (сжатие).

Погрешность: 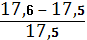* 100% = 0,6% 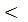1% (допустимо).

Моментная точка для определения N_HO – узел Е – на пересечении 2^х других перерезанных сил N_EK и N_EO.

∑ M_E^ост = R_А * 3 - * 3 – N_НО * h₂ = 0.

h₂ = |EH| = = 2,75 (м) – средняя линия трапеции.

N_НО = = = 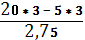16,4 (кН) (растяжение).

Из диаграммы: N_3-d = 16,5 (кН) (растяжение).

Погрешность: 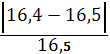* 100% = 0,6% 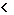1% (допустимо).

Приложение.

Не нашли, что искали? Воспользуйтесь поиском: