Смешанное соединение резисторов

Смешанным соединением называют сочетание последовательного и парал­лельного соединений резисторов. Большое разнообразие этих соединений не позволяет вывести общую формулу для определения эквивалентного сопро­тивления цепи. Поэтому в каждом конкретном случае, используя методы расчета при последовательном и параллельном соединениях, можно рассчитать эквива­лентное сопротивление при смешанном соединении. Поясним это на конкретном примере расчета электрической цепи (рис. 1.20 а).

Электрическую цепь постепенно упрощают и приводят к простейшему виду (рис. 1.20 б, в)

; ; ;

.

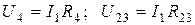Рис. 1.20

Проверка: 1) 2) .

1.8.4. Метод преобразований треугольника резисторов
в эквивалентную звезду и наоборот

Рассмотрим две электрические цепи (рис. 1.21). Одна из них имеет вид тре­угольника, другая – трехлучевой звезды. В дальнейшем такие соединения будем называть соответственно соединением в треугольник и соединением звездой.

Рис. 1.21

Соединения такого вида очень распространены в трехфазных цепях, в кото­рых часто возникает необходимость перехода от одного вида соединения к другому (эквивалентному). Эквивалентность треугольника и звезды резисторов заключается в том, что их замена не изменяет потенциалов узловых точек (φ_а, φ_b и φ_с), являющихся вершинами треугольника и эквивалентной звезды. Не изме­няются также токи, напряжения и мощности в остальной части схемы, не затро­нутой преобразованием.

Формулы пересчета без вывода сопротивлений ветвей треугольника 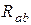, , 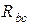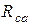в эквивалентную звезду , , имеют вид

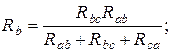
(1.39)

При переходе от звезды к треугольнику можно воспользоваться следую­щими формулами

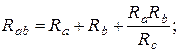
(1.40)

Если сопротивления всех ветвей цепи по схеме треугольник одинаковы, т.е. , сопротивления эквивалентной звезды будут также одина­ковые: , причем

.

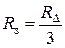1.8.5. Последовательное соединение источников
энергии

В практике последовательное и согласное включение источников приме­няют для увеличения напряжения. Рассмотрим схему с двумя согласно и одним встречно включенными источниками (рис. 1.22).

Рис. 1.22

По второму закону Кирхгофа запишем

. (1.41)

Отсюда

, (1.42)

где .

Напряжения на зажимах источников и приемника

.

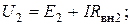
При последовательном соединении 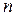источников с одинаковыми парамет­рами

. (1.43)

Не нашли, что искали? Воспользуйтесь поиском: