Синусоїдного струму.

Обсяг завдання. У відповідності до вихідних даних, вибраних із табл.5.3 згідно вказівок до вибору варіанта, провести аналіз електричного кола синусоїдного змінного струму зі змішаним з’єднанням елементів (рис. 5.11) наступним чином:

1) спростити електричну схему кола та визначити еквівалентний опір кола відносно затискачів джерела синусоїдного струму частотою f=50 Гц;

2) визначити струми та спади напруг усіх ділянок кола;

3) скласти баланс потужності джерела та споживачів, порівнявши окремо активні та реактивні потужності;

4) на комплексній площині побудувати суміщену векторну діаграми струмів і напруг.

Методичні рекомендації до розрахунків. На відміну від кіл постійного струму, де наявний тільки омічний опір R, в колах змінного струму розрізняють активний r (аналог омічного), реактивний х (індуктивний – та ємнісний – ) і повний Z опори. Разом з тим, методики розрахунків кіл змінного і постійного струму по суті аналогічні.

За послідовного з’єднання n активних r, індуктивних х _L та ємнісних х _C опорів, повний опір кола (ділянки кола) розраховують за формулою:

У розрахунках паралельного з’єднання використовують поняття провідності, якою є величина обернена до опору. Розрізняють провідності:

активна – реактивна – повна –

Струми та спади напруг на ділянках кола розраховують за законом Ома або з використанням законів Кірхгофа. Проте у разі застосування законів Кірхгофа діючі значення струмів і напруг, на відміну від кіл постійного струму, додають не алгебраїчно, а геометрично. Щоб зменшити похибку, геометричні дії з векторами електричних величин часто замінюють алгебраїчними операціями з комплексами цих величин. Звідси поділ методів розрахунку розгалужених кіл змінного струму на класичний (провідностей) та символічний (комплексних чисел).

Застосування комплексних чисел для розрахунків кіл синусоїдного струму дає можливість замінити диференційні рівняння, якими описуються процеси у цих колах, алгебраїчними рівняннями.

З курсу математики відомо, що синусоїдну функцію, зокрема обертовий

вектор (рис. 7.4), можна записати комплексним числом.

Відомо, що комплексне число може бути записано у алгебраїчній, показниковій та тригонометричній формах, відповідно:

; ; ,

де a та b – відповідно, дійсна та уявна складові комплексного числа (проекції вектора на вісі, відповідно, дійсних та уявних чисел); А – модуль комплексного числа (довжина вектора); y – аргумент комплексного числа (кут нахилу вектора до вісі дійсних чисел); – уявне число; е – основа натурального логарифму.

Для переходу від однієї форми запису комплексного числа до іншої використовують співвідношення:

, , , .

Комплекс діючого значення електричної величини, що змінюється у часі за синусоїдою, виділяють крапкою над символом, який відображає цю величину. Наприклад: – комплекс діючого значення струму; – комплекс діючого значення напруги тощо. Якщо електрична величина не є синусоїдною, то комплекс її значення виділяють рискою під символом, який відображає цю величину. Наприклад: Z – комплекс повного опору; S – комплекс повної потужності.

Додавати або віднімати комплексні числа зручніше, коли вони надані в алгебраїчній формі запису:

Множення або ділення цих чисел виконувати зручніше, коли воні надані у показниковій формі:

Комплекси величини, які відрізняються тільки за знаком аргументу, називають спряженими комплексами. В електротехніці спряжений комплекс звичайно виділяють «зірочкою» над символом величини. Так, якщо маємо

,

то спряжений комплекс буде:

Зазначимо, що при множенні комплексу величини на спряжений комплекс, в результаті одержимо квадрат модуля цієї величини –

.

Отже, використання символічного методу дає можливість суттєво скоротити розрахунок кола та одержувати результати у формі, більш прийнятній для аналізу процесів, які відбуваються у колі.

Методику використання методу для аналізу розгалуженого кола змінного струму покажемо на прикладі розрахунку схеми, утвореної шляхом спрощення (у розрахункову схему входять тільки ті елементи, значення яких в завданні не дорівнює нулю) загальної схеми (рис. 5.11).

Приклад.7.2. Розрахувати розгалужене коло змінного струму, схема якого має вигляд, показаний на рис.7.5., за наступних вихідних даних: U_АВ = 127 B, f = 50 Гц, r₀ = 2 Ом, r₂ = 18 Ом, r₃ = 17 Ом, L₀ = 16 мГн, L₁ = 24 мГн, L₂ = 32 мГн, С₁ = 300 мкФ, С₂ = 350 мкФ, С₃ = 400 мкФ.

Хід рішення:

За значеннями індуктивності L та ємності C розраховують реактивні опори ділянок кола, Ом:

;

;

;

;

;

і визначають комплекси повних опорів відповідних ділянок кола, Ом:

;

;

;

.

Подання опорів ділянок у вигляді комплексів повного опору дає підстави привести розрахункову схему до вигляду, зображеного на рис.7.6. Тут опори Z ₂ і Z ₃ ввімкнені паралельно. Врахувавши, що провідність даної ділянки -

знаходять її еквівалентний опір, Ом:

Тепер схема набуває вигляду, поданого на рис.7.7.

Подальша заміна ввімкнених послідовно опорів Z ₁, Z ₂₃ і Z ₀ еквівалентним опором кола Z _к, Ом:

^,

дає підстави спростити розрахункову схему до вигляду, зображеного на рис.7.8.

Якщо прийняти, що вектор спаду напруги кола АD спрямовано по осі дійсних чисел комплексної площини, то комплексна напруга (В) цієї ділянки буде:

Комплексний струму кола (А) та комплекси спадів напруг Ů_AB, Ů_BC та Ů_CD (В) на окремих ділянках кола розраховують за законом Ома:

;

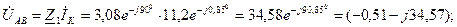
Правильність обчислення напруг Ů_AB, Ů_BC та Ů_CD перевіряють за другим законом Кірхгофа:

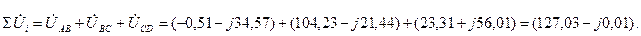
Для цього розраховують відносні розбіжності активних і реактивної складових ΣŮ _і та Ů_К:

Якщо виконуються умови Δ_а ≤ |1|% та Δ_р ≤ |1|%, то розрахунок кола можна продовжувати, а якщо ні - то слід зробити перевірку виконаних обчислень, починаючи з розрахунку комплексів повного опору ділянок кола.

Далі записують комплекс струму ділянок кола, А:

.

Враховуючи, що на ділянці ВС (рис. 7.6) вітки 2 і 3 ввімкнені паралельно та знаходяться під однаковою напругою, визначають струми віток так, А:

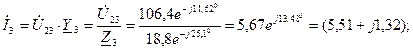
Правильність обчислення струмів перевіряють за І законом Кірхгофа:

.

Якщо відносні розбіжності активних і реактивних складових і не перебільшують ±1,0 %, то розрахунок кола можна продовжувати далі. У іншому випадку слід зробити перевірку виконаного розрахунку струмів віток 2 та 3.

Комплекс повної потужності S _дж (В А) джерела, його активну Р_дж та реактивну Q_дж складові визначаємо за формулою:

тут відповідно Р_дж = 3958,56 Вт та Q_дж = 2294,69 Вар.

Комплекс повної потужності S _сп (ВА) кола, тобто суму повних потужностей всіх споживачів, визначаємо шляхом додаванням їх активних Р_сп (Вт) та реактивних Q_сп (Вар) складових:

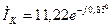Зверніть увагу: обчислюючи S _дж, використовують спряжений комплекс від струму кола , а, обчислюючи S _сп, до квадрату беруть тільки модуль комплексу струму кола, наприклад модуль комплексу струму I₁=11,22 від струму

Задачу вважають розв’язаною правильно, якщо для відносних розбіжностей активних і реактивних складових S _дж та S _сп виконуються умови:

За результатами розрахунків, на комплексній площині будують суміщену діаграму струмів та напруг кола (рис. 7.9). Методика побудови векторів діаграми така:

спочатку обирають зручні масштаби побудови векторів струму М_і (А/мм) і напруги М_u (В/мм) та вказують їх на комплексній площині;

далі необхідно:

1) з початку координат по осі дійсних чисел (y_uк=0) відкласти відрізок завдовжки 110/М_u ;

2) з початку координат, під кутом y_u1= - 14,9^° до осі дійсних чисел відкласти відрізок довжиною 294,06/М_u;

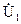3) з кінця під кутом y_u23= - 23,46^° до осі дійсних чисел відкласти відрізок довжиною 189,83/ М_u;

4) з початку координат, під кутом y_ік=y_і1= - 45^° до осі дійсних чисел відкласти відрізок довжиною 15,56/ М_і;

5) з початку координат під кутом y_і2= - 82,49^° до осі дійсних чисел відкласти відрізок довжиною 16,28/М_і ;

6) з кінця під кутом y_і3= 30,29^° до осі дійсних чисел відкласти відрізок довжиною 10,21/М_і.

Зверніть увагу: за правильного виконання дій в загальному випадку на суміщеній діаграмі отримують два замкнених багатокутника, один з яких складений з векторів напруг, а другий – з векторів струмів (у даному випадку маємо трикутник струмів та трикутник напруг).Суміщена векторна діаграма дає можливість наочно аналізувати характери навантажень ділянок кола. Так, в даному разі, розрахункова схема в цілому має активно-індуктивний характер навантаження, оскільки вектор струму кола відстає від вектора напруги кола на кут:

Перша ділянка схеми, де включені активний опір r₁, індуктивність L₁ та ємність C₁, також має активно-індуктивний характер навантаження, оскільки вектор діючого тут струму відстає від вектора напруги на кут

Одна з паралельних віток (Z ₂) кола має активно-індуктивний характер навантаження. Тут кут зсуву фаз між векторами і додатний:

В іншій паралельній вітці (Z ₃) характер навантаження активно-ємнісний і кут зсуву фаз між 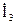та є від’ємний:

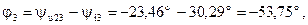
У сукупності ж ділянка кола, що складається з двох паралельних віток 2 і 3, має активно-індуктивний характер навантаження. Тут відстає від на кут

Не нашли, что искали? Воспользуйтесь поиском: