СРЕДНЯЯ КВАДРАТИЧНАЯ ОШИБКА.

При ответственных измерениях, когда необходимо знать надежность полученных результатов, используется средняя квадратичная ошибка s (или стандартное отклонение), которая определяется формулой

(5)

Величина s характеризует отклонение отдельного единичного измерения от истинного значения.

Если мы вычислили по n измерениям среднее значение 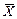по формуле (2), то это значение будет более точным, то есть будет меньше отличаться от истинного, чем каждое отдельное измерение. Средняя квадратичная ошибка среднего значения 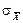равна

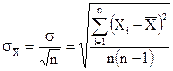(6)

где s - среднеквадратичная ошибка каждого отдельного измерения, n – число измерений.

Таким образом, увеличивая число опытов, можно уменьшить случайную ошибку в величине среднего значения.

В настоящее время результаты научных и технических измерений принято представлять в виде

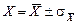(7)

Как показывает теория, при такой записи мы знаем надежность полученного результата, а именно, что истинная величина Х с вероятностью 68% отличается от 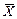не более, чем на .

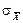При использовании же средней арифметической (абсолютной) ошибки (формула 2) о надежности результата ничего сказать нельзя. Некоторое представление о точности проведенных измерений в этом случае дает относительная ошибка (формула 4).

При выполнении лабораторных работ студенты могут использовать как среднюю абсолютную ошибку, так и среднюю квадратичную. Какую из них применять указывается непосредственно в каждой конкретной работе (или указывается преподавателем).

Обычно если число измерений не превышает 3 – 5, то можно использовать среднюю абсолютную ошибку. Если число измерений порядка 10 и более, то следует использовать более корректную оценку с помощью средней квадратичной ошибки среднего (формулы 5 и 6).

Не нашли, что искали? Воспользуйтесь поиском: