Расчетное задание № 2 «Расчет характеристик случайных сигналов при их оптимальной обработке».

Расчетное задание № 1 «Расчет характеристик случайных величин и процессов».

Задача №1

Дискретная случайная величина задана плотностью распределения вероятности

,

где , а - дельта-функция Дирака.

Непрерывная случайная величина задана гауссовской плотностью распределения вероятности

.

Случайные величины и независимы.

Найти плотность распределения вероятности суммы этих случайных величин . Вычислить и представить в виде таблицы математические ожидания и дисперсии всех трех случайных величин .

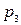
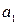
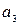
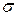
0,4	0,25	–			–7	–3

Решение

=

=

= = +

=

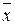X и Y- независимые некоррелированные

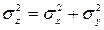
Подставляя численные значения, получим:

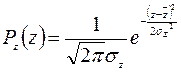
Сведем полученные значения в таблицу:

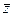
0,6	–3	–2,4	63,64		38,64

Задача № 2

Непрерывные случайные величины и заданы плотностями распределения вероятности

,

.

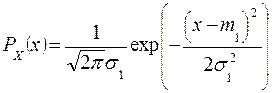Случайные величины и независимы.

Найти плотность распределения линейной комбинации этих случайных величин . Вычислить и представить в виде таблицы математические ожидания и дисперсии всех трех случайных величин .

–1					–4

Решение

,

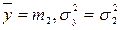
X и Y- независимые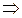

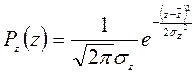
Подставим численные значения:

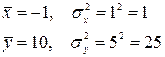
Сведем полученные значения в таблицу:

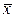
–1		–42

Задача № 3

Реализация квазидетерминированного случайного процесса определяется следующим выражением

.

Комплексная огибающая любой реализации .

Cовместная плотность распределения вероятности синфазной 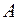и квадратурной компонент этого процесса является гауссовской и определяется выраженим

.

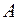Здесь – корреляционная матрица распределения синфазной и квадратурной компонент, а .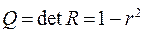

Комплексная огибающая реализации преобразуется по правилу , – фиксированная фаза. Тем самым образуется новый квазидетерминированный случайный процесс, реализация которого определяется следующим выражением

.

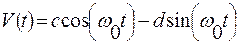Для исходного и полученного случайных процессов вычислить и свести в таблицу математические ожидания и дисперсии синфазной и квадратурной составляющих и корреляционные моменты между синфазной и квадратурной составляющими:

.

Записать выражение для совместной плотности распределения синфазной и квадратурной компонент нового процесса. Подставить в это выражение

Вычислить математические ожидания и дисперсии исходного и полученного процессов:

.

Вычислить авто- и взаимнокорреляционные функции исходного и полученного процессов:

Записать корреляционные функции в виде формул. Подставить численные значения.

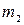
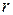
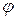
–1				0,6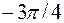

Решение

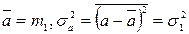
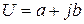
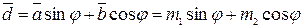
Подставим численные значения:

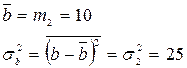
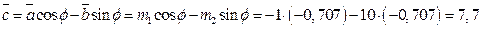
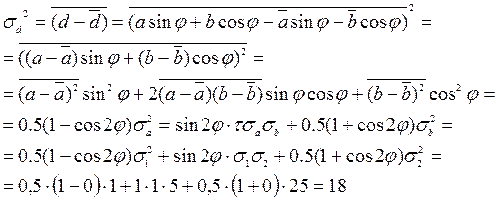
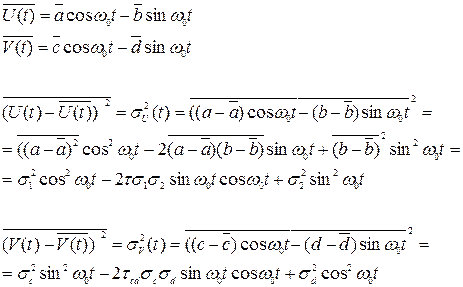
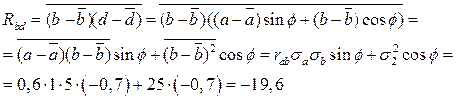
Сведем полученные значения в таблицы:

-1

7,7	–6,3	9,8		–12

Расчетное задание № 2 «Расчет характеристик случайных сигналов при их оптимальной обработке».

Задача №1

1.1 Помехоустойчивость сигналов при когерентном приеме определяется следующими выражениями

,

,

.

В последних выражениях означают фазовую, частотную и амплитудную манипуляцию соответственно.

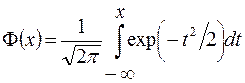- функция ошибок,

, ,

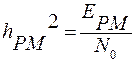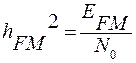Считая, что 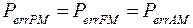, а также известным одно из значений , найти две неизвестные из величин .

1.2 Помехоустойчивость сигналов при некогерентном приеме определяется следующими выражениями

, .

Считая, что , а также известным 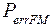найти .

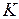
–	–			–3

Решение

1.1

отсюда

1.2

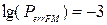
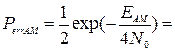
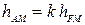
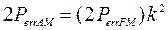
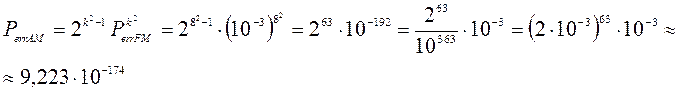
Сведем полученные значения в таблицу:

Задача №2

Рассматривается задача обнаружения сигнала как задача проверки простой гипотезы против простой альтернативы 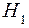. Гипотеза соответствует случаю отсутствия сигнала. Гипотеза 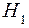соответствует случаю наличия сигнала. В приемнике измеряется только одно отсчетное значение напряжения 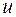. Считается, что шум является гауссовским. Поэтому соответствующие условные плотности распределения задаются выражениями:

,

.

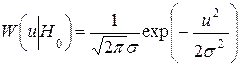Вероятность ложной тревоги определяется выражением

.

Вероятность пропуска определяется выражением

.

Области интегрирования в обоих случаях определяются порогом напряжения и знаком напряжения .

Представить вероятности ложной тревоги и пропуска сигнала в виде формул с явным заданием пределов интегрирования, вычислить в среде Матлаб и представить в виде графиков в диапазоне порогов .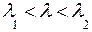

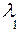
–3	0,6	–2	–1

Решение

Представить и построить график.

– интеграл вероятности

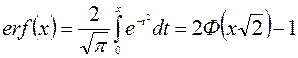– функция ошибки

– остаточная функция ошибки

Так как , то

Получаем следующий график:

Код программы:

>> clear all;

>> m = -3;

>> sigma = 0.6;

>> lambdad = [-2 -1];

>> lamin = lambdad(1);

>> lamax = lambdad(2);

>> lams = (lamax - lamin)/500;

>> la = lamin:lams:lamax;

>> sq = sqrt(2);

>> arg1 = la/sigma;

>> fla1 =.5 +.5*erf(arg1/sq);

>> arg2 = (la - m)/sigma;

>> fla2 =.5 +.5*erf(arg2/sq);

>> if(m>0)alp = 1 - fla1;

bet = fla2;

end;

>> if(m<0)alp = fla1;

bet = 1 - fla2;

end;

>> figure(1);

>> hold on;

>> plot(la, alp, 'r', 'LineWidth', 3);

>> plot(la, bet, 'g', 'LineWidth', 3);

>> grid on;

>> hold off;

Задача №3

Cлучайный процесс (полезный сигнал) характеризуется односторонним спектром мощности следующего вида:

.

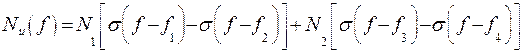Cлучайный процесс (помеха) характеризуется односторонним спектром мощности следующего вида:

.

В двух последних выражениях - функция Хевисайда. Частотный коэффициент передачи линейной системы, минимизирующей дисперсию ощибки, имеет тождественно равную нулю ФЧХ. АЧХ этой системы задается выражением:

.

При этом предельно допустимая дисперсия ошибки определяется выражением:

.

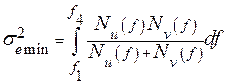Представить в виде формулы с явным заданием его значений в разных частотных диапазонах. Вычислить соответствующее значение .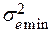

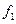
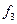
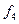
Решение

Итак,

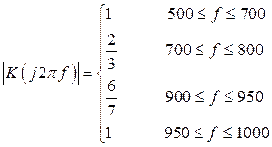
Получаем следующий график:

Код программы:

>> clear all;

>> nuU = [10 30 5];

>> fuU = [500 800 900 1000 700 950];

>> delf = max(fuU) - min(fuU);

>> fmin = min(fuU) -.2*delf;

>> fmax = max(fuU) +.2*delf;

>> hf = (fmax - fmin)/5000;

>> f = fmin:hf:fmax;

>> nu1 =.5*nuU(1)*(sign(f-fuU(1)) - sign(f-fuU(2)));

>> nu2 =.5*nuU(2)*(sign(f-fuU(3)) - sign(f-fuU(4)));

>> nu = nu1 + nu2; % signal

>> nU =.5*nuU(3)*(sign(f-fuU(5)) - sign(f-fuU(6)));

>> figure (2);

>> hold on;

>> plot(f, nu, 'k', 'LineWidth', 2);

>> plot(f, nU, 'k', 'LineWidth', 2);

>> hold off;

Список литературы

1. В.А. Борисов. Радиотехнические системы передачи информации: учебное пособие для вузов / Борисов В.А., Калмыков В.В., Ковальчук В.М., Себекин Ю.Н., Сенин А.И., Федоров И.Б., Цикин И.А. – М.: Радио и связь, 1990. – 304 с.

2. Л.А. Мироновский. Введение в Matlab: учебное пособие / Мироновский Л.А., Петрова К.Ю. – СПб.: СПбГУАП, 2005. – 122 с.

3. С.И. Баскаков. Радиотехнические цепи и сигналы / Баскаков С.И. – М.: Высшая школа, 2000. – 462 с.

Не нашли, что искали? Воспользуйтесь поиском: