
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Краткий справочник по Си
Алфавит языка Си составляют 52 (заглавные и прописные) латинские буквы, 10 арабских цифр, 30 знаков и символов:
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | |||
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z | |||
| + | плюс; | _ | пробел; | |||||||||||||||||||||||||
| - | минус; | ( | левая круглая скобка; | |||||||||||||||||||||||||
| * | звездочка; | ) | правая круглая скобка; | |||||||||||||||||||||||||
| / | косая черта; | [ | левая квадратная скобка; | |||||||||||||||||||||||||
| \ | обратная косая черта; | ] | правая квадратная скобка; | |||||||||||||||||||||||||
| < | меньше; | { | левая фигурная скобка; | |||||||||||||||||||||||||
| > | больше; | } | правая фигурная скобка; | |||||||||||||||||||||||||
| = | равно; | ? | знак вопроса; | |||||||||||||||||||||||||
| . | точка; | ! | восклицательный знак; | |||||||||||||||||||||||||
| , | запятая; | | | вертикальная черта; | |||||||||||||||||||||||||
| ; | точка с запятой; | ~ | волнистая черта; | |||||||||||||||||||||||||
| : | двоеточие; | ^ | угол вверх; | |||||||||||||||||||||||||
| ' | апостроф; | # | решетка; | |||||||||||||||||||||||||
| " | кавычки; | & | амперсант; | |||||||||||||||||||||||||
| _ | подчеркивание; | % | процент. | |||||||||||||||||||||||||
К основным ключевым слова м относятся:
| auto | автоматический | if | если |
| break | завершить | int | целое |
| case | вариант | long | длинное |
| char | символьный | register | регистровый |
| continue | продолжить | return | возврат |
| default | по умолчанию | short | короткий |
| do | выполнять | sizeof | размер |
| double | двойной точности | static | статический |
| else | иначе | struct | структура |
| entry | вход | switch | переключатель |
| extern | внешний | typedef | определение типа |
| for | для | union | объединение |
| float | плавающий | unsigned | без знака |
| goto | перейти | while | пока |
Типы переменных определяют размеры ячеек для хранения их значений.
| Описатель | Наименование типа | Число байт (бит) |
| short int | Короткий целый | 2 (16) |
| int | Целый | 2 (16) |
| long int | Длинный целый | 4 (32) |
| float | Плавающая точка | 4 (32) |
| double | Двойная точность | 8 (64) |
| char | Символьный | 1 (8) |
Библиотека системных функций языка Си
| Математическая запись | Вызов функции | Наименование функции |
| ln x | log(x) | Натуральный логарифм |

| log10(а) | Десятичный логарифм |
| e0.5 | exp(0.5) | Экспонента |
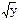
| sqrt(y) | Корень квадратный |
| sin x | sin(х) | Синус |
| cos в | cos(в) | Косинус |
| tg(x+с) | tan(x+с) | Тангенс |
| arcsin x | asin(x) | Арксинус |
| arccos в | acos(в) | Арккосинус |
| arctg с | atan(c) | Арктангенс |
| xy | pow(x,y) | Возведение в степень |
| | x | | fabs(x) | Нахождение абсолютного значения х |
Правила записи и вычисления арифметических выражений
1. Арифметические выражения записываются одноэтажно. Например, 0.35+а*2-cos(b)/(PI+2).
2. Все знаки арифметических операций указываются явно. Например, А+В+С не равно АВ+С, так как во втором случае подразумевается переменная с именем АВ, а не две переменные.
3. Запись подряд двух знаков операций, как правило, запрещается (исключение см. разд. 6.2.1). Обойти это правило можно с помощью круглых скобок. Например, a*(-b).
4. Арифметическое выражение может быть любой сложности. Минимально может состоять из одного операнда. Реально определяется математической моделью задачи. Если зависимости математической модели относительно громоздки, рекомендуется представлять одну сложную зависимость несколькими простыми, – содержащими не более 5 – 7 операций в каждой.
5. Последовательность выполнения операций в арифметическом выражении соответствует принятой в математике:
· выражения в скобках;
· вычисления функций;
· умножения, деления;
· сложения, вычитания.
Например, выражение 0.2-cos(0.5)*pow(v,3) выполняется в следующем порядке: вычисление косинуса, возведение v в куб, умножение первого результата на второй и, наконец, вычитание из константы 0.2 константы, полученной после умножения.
6. Одноранговые операции выполняются слева направо. Например, выражение А*В/С*3 будет выполняться в порядке записи.
7. При необходимости нарушить последовательность выполнения действий используют скобки. Например, А+В/(С+D) или (0.2-v)*cos(0.5).
8. При делении целого операнда на целый от частного используется только целая часть. Так, результатом вычисления 5/2 будет целая константа 2, а выражения 2/5 – ноль. Для получения истинного результата необходимо сделать вещественными оба операнда или один из них. Например, 5./2. или 5./2 (5/2.).
9. Возведение в степень (pow(a,x)), если показатель (х) целочисленный, выполняется методом последовательного умножения. Если показатель степени вещественный, возведение осуществляется по формуле ax = еxlna. Использование функций (экспоненты и логарифма) приводит к получению приближенного значения результата.
10.В арифметическом выражении желательно использовать операнды одного типа. Например, i+23*k, если переменные i, k – целые или x*2.-0.36/cos(y), если переменные x, y – вещественные. В первом случае результатом будет целая константа, во втором – вещественная константа двойной точности (перед использованием автоматически все вещественные операнды приводятся к типу double).
11.Допускается применение смешанных арифметических выражений. При этом наличие хотя бы одного вещественного операнда приводит к получению результата (константы) с двойной точностью. Например, при вычислении выражения 4/z+i*k-0.07*sin(3./b) результатом будет вещественная константа двойной точности, если переменные i, k – целые, а z, b – вещественные. Аналогично, возможно получение дробного результата деления целых переменных использованием дополнительного операнда в виде вещественной константы (1.). Так, если переменные i и k описаны как целые, то результат выражения i/k есть целая константа (целая часть частного), а результат выражения i*1./k есть вещественная константа двойной точности. Следует помнить, что наличие операции деления двух целых операндов в смешанном выражении может привести к неверному результату. Например, вычисление выражения 0.02 + 3/5 - 0.01 дает неверный результат (0.01) т.к. второе слагаемое (частное от деления целой константы 3 на целую константу 5) – равно нулю.
12.Деление по модулю % используют в целочисленной арифметике. Результат операции– остаток от деления целого операнда, записанного слева от знака операции на операнд справа от него. Например, выражение 13%5 дает результат 3, поскольку 13=5*2+3, где 3 – остаток от деления.
13.Вычисление корня n-ой степени при n>2 требует предварительного преобразования его к виду  , а затем использование функции возведения в степень. Например, зависимость
, а затем использование функции возведения в степень. Например, зависимость 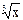 должна быть преобразована к виду
должна быть преобразована к виду  , а затем сформирована как вызов функции pow(x,1./3.) Попытка вычисления функции вида pow(x,1/3) приведет к получению неверного результата – единицы т.к. показатель степени (1/3) после деления станет равен нулю.
, а затем сформирована как вызов функции pow(x,1./3.) Попытка вычисления функции вида pow(x,1/3) приведет к получению неверного результата – единицы т.к. показатель степени (1/3) после деления станет равен нулю.
Оператор присваивания
Структура оператора:
П=А; (П=L;)
где П – имя переменной;
А (L) – арифметическое (логическое) выражение;
= – символ операции присваивания;
; – символ оператора.
Оператор ввода
Структура оператора:
scanf(“управляющая строка”, АП1 [, АП2,., АПn]);
, где scanf – имя функции (считать);
“управляющая строка” – список спецификаторов вводимых переменных, оформленный в виде символьной строки;
АП1 АП2 АПn – список адресов вводимых переменных;
,, – разделители списка;
() – ограничители аргументов функции scanf;
[ ] – признак необязательности содержимого;
; – символ оператора.
Простейший спецификатор ввода точность не учитывает и имеет вид:
%[длина]тип
, где % – признак спецификатора;
длина – целая константа без знака, определяющая количество считываемых символов численного значения;
тип – буквенное обозначение типа переменной;
[ ] – признак необязательности содержимого.
| Тип переменной | Обозначение типа | Формат ввода |
| int | d | Целое десятичное |
| long | ld | Длинное целое десятичное |
| float | f (e) | Вещественное десятичное с обычной точностью |
| double | lf | Вещественное десятичное с двойной точностью |
Оператор вывода на дисплей
Структура оператора:
printf(“управляющая строка” [, П1,..., Пn]);
, где printf – имя функции (“напечатать”);
“управляющая строка” – список спецификаторов выводимых переменных, оформленный в виде символьной строки;
П1...Пn – список идентификаторов выводимых переменных;
,, – разделители идентификаторов в списке;
() – ограничители аргументов функции printf;
[ ] – признак необязательности содержимого;
; – символ оператора.
Структура спецификатора вывода (упрощённая):
%[длина][.точность]тип,
, где % – признак спецификатора;
длина – целая константа без знака, определяющая общий размер поля выводимой переменной (количество разрядов численного значения с учетом разделителя, знаков  и буквы Е (е), если они имеются);
и буквы Е (е), если они имеются);
точность – целая константа без знака, определяющая число разрядов дробной части мантиссы численного значения переменной;
. – разделитель длины и точности;
тип – буквенное обозначение типа переменной;
[ ] – признак необязательности содержимого.
При выводе часто используют следующие обозначения типа
Не нашли, что искали? Воспользуйтесь поиском: