Черт. 27. К примеру расчета 16

Пример 16. Дано: железобетонная балка моно­литного перекрытия с размерами поперечного сечения по черт. 27, а; расположение отогнутых стержней — по черт. 27, б; временная эквивалент­ная нагрузка на балку v = 96 кН/м, постоянная — g = 45 кН/м; поперечная сила на опоре Q_max = 380 кН; бетон тяжелый класса В15 (R_bt = 0,67 МПа при g _{b 2} = 0,9); хомуты двухветвевые диаметром 6 мм (A_sw = 57 мм ²) из арматуры клас­са А- I (R_sw = 175 МПа), шагом s = 150 мм; отогну­тые стержни класса А-II (R_sw = 225 МПа), пло­щадью сечения: первой плоскости А _{s,inc 1} = 628 мм ² (2 Æ 20), второй — А _{s,inc 2} = 402 мм ² (2 Æ 16).

Требуется проверить прочность наклонных сече­ний по поперечной силе.

Расчет. h ₀ = 600 – 40 = 560 мм. Согласно п. 3.31 находим значения M_b и q_sw:

(см. табл. 21);

мм;

Н/мм.

Согласно п. 3.32 находим q ₁ = g + v /2 = 45 + 96/2 = 93 кН/м.

Проверим из условия (50) с учетом формулы (65) наклонное сечение с длиной проекции, равной расстоянию от опоры до конца второй плоскости отгибов, т. е. при с = 50 + 520 + 300 = 870 мм = 0,87 м.

Поперечная сила на расстоянии с = 0,87 м от опо­ры равна:

кН.

Определим проекцию опасной наклонной тре­щины c ₀ согласно п. 3.35.

Сначала определим максимальное значение c ₀ по формуле (56):

принимаем c _{0, max} = 1,12 м. Поскольку с = 0,87 м < c _{0 ,max} = 1,12 м, принимаем для этого наклонного сечения c ₀ = с = 0,87 м. Наклонную тре­щину, расположенную между концом второй и нача­лом первой плоскостей отгибов, т. е. не пересека­ющую отгибы, в расчете не рассматриваем, так как для нее c ₀ = 0, 30 м < c _{0 ,max} .

Для первой плоскости отгибов

Тогда

т. е. прочность данного наклонного сечения обес­печена.

Проверим наклонное сечение, оканчивающееся на расстоянии c ₀ = 1,12 м от начала первой плоско­сти отгибов, т.е. при с = 0,05 + 0,52 + 1,12 = 1,69 м.

Поперечная сила на расстоянии с = 1,69 м от опо­ры равна Q = 380 – 93 · 1,69 = 222,8 кН.

Для второй плоскости отгиба

Для этого сечения принимаем наклонную трещи­ну, проведенную от конца наклонного сечения до начала первой плоскости отгибов, т.е. c ₀ = c _{0 ,max} = 1,12 м. Наклонные трещины, проведен­ные от конца наклонного сечения до опоры и до на­чала второй плоскости отгибов, не рассматриваем, так как в первом случае c ₀ = с = 1,69 м > c _{0 ,max} = 1,12 м, а во втором — трещина не пересекает отги­бы при c ₀ < c _{0 ,max} .

Тогда

т. е. прочность данного наклонного сечения обеспе­чена.

Проверим наклонное сечение, оканчивающееся на расстоянии c _{0 ,max} = 1,12 м от начала второй плоскости отгибов, т. е. при с = 0,05 + 0,52 + 0,30 + 0,52 + 1,12 = 2,51 м.

Поперечная сила на расстоянии с = 2,51 м от опо­ры равна Q = 380 – 93 · 2,51 = 146,6 кН.

Для этого сечения, очевидно, c ₀ = c _{0 ,max} = 1,12 м и наклонная трещина отгибы не пересекает, т. е. Q_s,inc = 0. Поскольку c = 2,51 м 1,87 м, принимаем Q_b = Q_b,min = 7 6,5 кН

Тогда Q_b + q_swc ₀ + Q_s,inc = 76,5 + 66,5 · 1,12 + 0 = 151 кН > Q = 146,6 кН, т. е. прочность любых наклонных сечений обеспечена.

Согласно п. 3.29 проверим расстояние между началом первой плоскости отгибов и концом второй плоскости, принимая поперечную силу у конца второй плоскости отгибов Q = 299,1 кН и j _{b 4} = 1,5:

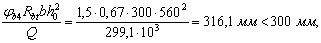
т. е. требование п. 3.29 выполнено.

Пример 17. Дано: железобетонная двускатная бал­ка покрытия пролетом 8,8 м; сплошная равномерно распределенная нагрузка на балку q = 46 кН/м (черт. 28, a); размеры поперечного сечения — по черт. 28, б; бетон тяжелый класса В25 (R_bt = 0,95 МПа при g _{b 2} = 0,9); хомуты из арматуры класса А- I (R_sw = 175 МПа), диаметром 8 мм (A_sw = 50,3 мм ²), шагом s = 150 мм.

Требуется проверить прочность наклонных сече­ний по поперечной силе.

Не нашли, что искали? Воспользуйтесь поиском: