Черт. 55. Расположение расчетных пространственных сечений

Й схемы в балке, нагруженной сосредоточенными

Силами

1, 2 ¾ расчетные пространственные сечения; M ₁, T ₁, Q ₁ ¾

расчетные усилия для пространственного сечения 1;

М ₂, Т ₂, Q ₂ ¾ то же, для пространственного сечения 2

б) для элементов, нагруженных только равномерно распределенной нагрузкой q, если в пролетном сечении с наибольшим изгибающим моментом M_max имеет место крутящий момент Т ₀, ¾ из условия

(174)

где t ¾ равномерно распределенный крутящий момент на единицу длины элемента.

Прочность по продольной арматуре, расположенной у сжатой от изгиба грани, рекомендуется проверять для свободно опертых балок из условия (173), принимая усилия Т и Q в опорном сечении при M_max = 0.

Если на рассматриваемых участках выполняется условие

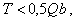(175)

продольную арматуру можно проверить только из условия чистого изгиба (см. п. 3.15).

Прочность по поперечной арматуре, расположенной у любой грани шириной b, рекомендуется проверять из условия

(176)

Примечание. Подобранную из условия (173) продольную арматуру можно несколько уменьшить, если невыгоднейшее пространственное сечение длиной проекции с ₁, равной:

(177)

выходит за пределы длины элемента или его участка с однозначными и ненулевыми значениями Т. В этом случае расчет производится общим методом согласно п. 3.84 при соответственно уменьшенной длине проекции с ₁.

3.86. Расчет пространственного сечения по 2-й схеме (см. черт. 53) производится из условия

(178)

при этом значение R_sA_{s 2} принимается не более 2 q_{sw 2} h, а значение q_{sw 2} ¾ не более

В условии (178):

A_{s 2} ¾ площадь сечения всех растянутых продольных стержней, расположенных у грани шириной h, параллельной плоскости изгиба;

с ₂ ¾ длина проекции на продольную ось элемента линии, ограничивающей сжатую зону пространственного сечения; невыгоднейшее значение с ₂определяется по формуле

(179)

и принимается не более 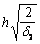и не более 2 b + h, при этом пространственное сечение не должно выходить за пределы элемента и его участка с однозначными и ненулевыми значениями Т;

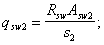(180)

где A_{sw 2} ¾ площадь сечения одного поперечного стержня, расположенного у грани шириной h;

s ₂ ¾ расстояние между поперечными стержнями, расположенными у грани шириной h;

(181)

а ₂ ¾ расстояние от грани шириной h до оси продольных стержней, расположенных у этой грани.

Крутящийся момент Т и поперечная сила Q принимаются в поперечном сечении, проходящем через середину пространственного сечения (см. черт. 54, б).

В случае, когда удовлетворяется условие (175), расчет пространственного сечения по 2-й схеме не производится. Вместо него производится расчет наклонных сечений согласно пп. 3.31 ¾3.38 без учета отогнутых стержней. При этом в соответствующих формулах к поперечной силе Q добавляется величина (где Т ¾ крутящийся момент в том же поперечном сечении, что и Q), а величина q ₁ умножается на коэффициент 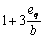(где e_q ¾ эксцентриситет попереч­ной равномерно распределенной нагрузки q, вызывающий кручение элемента). В случае, если Т < 0,25 Qb, при расчете наклонных сечений можно учитывать наличие отогнутых стержней.

3.87. Необходимую из расчета пространственного сечения по 2-й схеме интенсивность хомутов допускается определять по формулам:

при

(182)

при 1,75 ³ j _t > 1

(183)

где T, Q ¾ максимальные значения соответственно крутящего момента и поперечной силы на рассматриваемом участке.

При j _t > 1б75 следует увеличить площадь сечения арматуры A_{s 2} или размер сечения b так, чтобы было выполнено условие j _t £ 1,75.

Если поперечная нагрузка приложена в пределах высоты сечения и действует в сторону растянутой зоны, интенсивность вертикальных хомутов должна быть увеличена по сравнению с вычисленной по формулам (182) и (183) в соответствии с расчетом на отрыв согласно п. 3.97.

Не нашли, что искали? Воспользуйтесь поиском: