
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Формальная постановка задачи.
Дано у-ние:
Первая производная f(x)=x+3lgx-5+0, в интервале [1;5]
x=3,404_022_669_1
Уточнение корня методом касательных (метод Ньютона).
 Метод касательных, связанный с именем И.Ньютона, является одним из наиболее эффективных численных методов решения уравнений. Идея метода очень проста. Предположим, что функция f(x), имеющая корень на отрезке [a; b], дифференцируема на этом отрезке и ее производная f¢(x) не обращается на нем в нуль. Возьмем произвольную точку х0 проведем касательную к графику функции f(x) в этой точке и запишем уравнение касательной:
Метод касательных, связанный с именем И.Ньютона, является одним из наиболее эффективных численных методов решения уравнений. Идея метода очень проста. Предположим, что функция f(x), имеющая корень на отрезке [a; b], дифференцируема на этом отрезке и ее производная f¢(x) не обращается на нем в нуль. Возьмем произвольную точку х0 проведем касательную к графику функции f(x) в этой точке и запишем уравнение касательной:
y=f(x0)+f¢(x0)(x-x0) (7)



 |
Найдем точку пересечения касательной с осью абсцисс – х1. Для определения координаты этой точки можем использовать уравнение
f(x0)+f¢(x0)(x-x0)=0
Таким образом,
x1=x0-  (8).
(8).
Повторим проделанную процедуру: напишем уравнение касательной к графику функции в точке х1 и найдем точку пересечения этой касательной с осью Ох (см. рис.1):
х2=x1- 
Продолжая этот процесс, получим последовательность {хn}, определенную с помощью рекуррентной формулы:
xn+1=xn- 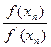 , n=0,1,2,… (9).
, n=0,1,2,… (9).
3.Данные
| Обозначение | Структурный тип | Назначение |
| Х0 | Вещественное число | Вводимая переменная. |
| eps | Вещественное число | Машинный ноль |
| X1 | Вещественное число | Вспомогательная переменная |
| X2 | Вещественное число | Вспомогательная переменная |
| Proverka | Вещественное число | Проверка приближения |
4.Алгоритмизация
5.Программирование
uses Crt;
Var xn,xn1,a,b,c: real;
function f1(x:Real):Real; {Функция}
begin
f1:=x+3*ln(x)/ln(10)-5;
end;
function f2(x:Real):Real; {Производная функция}
begin
f2:=1+3/(x*ln(10));
end;
begin
a:=1;
b:=5;
c:=0.00000001;
writeln(' A=',a,' B=',b);
writeln (Точность вычислений c=',c);
xn:=a;
xn1:=xn-f1(xn)/f2(xn);
Writeln('xn=',xn,' f(xn)=',f1(xn));
while (ABS (f1(xn))>c) and (xn<=b) do
begin
xn:=xn1;
xn1:=xn-f1(xn)/f2(xn);
Writeln('xn=',xn,' f(xn)=',f1(xn));
end;
writeln ('xn+1=',xn1,' f(xn+1)=',f1(xn1));
Readln;
end.
6.Испытание программы
1)eps=0.000001 xn+1=3.40402266915563 f(xn+1)=0
2)eps=0.1 f(xn+1)=-2.89425316459813E-5
7.Заключение
Программа отлажена и работает без сбоев.
| <== предыдущая лекция | | | следующая лекция ==> |
| Система Турбо-Паскаль. | | | Функциональная схема ЭВМ. |
Не нашли, что искали? Воспользуйтесь поиском: