
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Одномерная кривая в пространстве
plot3(x,y,z) или comet3(x,y,z)
Пример
t=0:0.1:30; x=0.1*t.*cos(t); y=0.1*t.*sin(t); z=0.05*t; hl=plot3(x,y,z); grid on; axis square;

Рис. 17. plot3(x,y,z)

Рис. 18. comet3(x,y,z)
Сеточные поверхности
Функция изображения поверхности: mesh(z)
Необходимо знать разбиение x и y. Т.е. в начале делаем [xx, yy]=meshgrid(x, y), потом рассчитывается z=f(x, y).
Meshgrid
Синтаксис:
[X, Y] = meshgrid(x, y)
[X, Y] = meshgrid(x)
[X, Y, Z] = meshgrid(x, y, z)
Описание:
Функция [X, Y] = meshgrid(x, y) формирует двумерные массивы X и Y, которые определяют координаты узлов прямоугольника, задаваемого векторами x и y. Этот прямоугольник задает область определения функции от двух переменных, которую можно построить в виде 3D-поверхности.
Функция [X, Y] = meshgrid(x) является сокращенной формой записи функции [X, Y] = meshgrid(x, x).
Функция [X, Y, Z] = meshgrid(x, y, z) формирует массивы X, Y и Z, которые определяют координаты узлов параллелепипеда, задаваемого векторами x, y и z. Этот параллелепипед задает область определения для вычисления функции от трех переменных и построения 3D-параметрических поверхностей.
Пример:
Вычисление функции в области -2 < x < 2, -2 < y < 2:
[X, Y] = meshgrid(-2:.2:2, -2:.2:2);
Z = X.*exp(-X.^2 - Y.^2);
mesh(Z)

Рис. 20.
x=-2:0.1:2; y=x; [xx, yy]=meshgrid(x,y); z=exp(-xx.^2-yy.^2); subplot(2,2,1); mesh(z);
subplot(2,2,2); surf(z);
subplot(2,2,3); surf(z); shading flat;
subplot(2,2,4); surf(z); shading interp;

Рис. 21.
[X,Y] = meshgrid(-3:.125:3);
Z = peaks(X,Y);
meshc(X,Y,Z);
axis([-3 3 -3 3 -10 5])
meshc - в дополнение к трехмерным поверхностям строит проекцию линий постоянного уровня

Рис. 22.
Изолинии
Для отрисовки изолиний используются contour(z); contour(z,N); contour(z,value);
value - вектор значений
[x,y]=meshgrid(linspace(0,2*pi,30),linspace(0,pi,30)); z=sin(x).*cos(y+pi/2);
contour(x,y,z,[-1:0.1:-0.1 0.1:0.1:1]);
xlabel('x');
ylabel('y');
title('Contour of z = sin(x).*cos(y+pi/2)');
linspace - формирование линейного массива равноотстоящих узлов
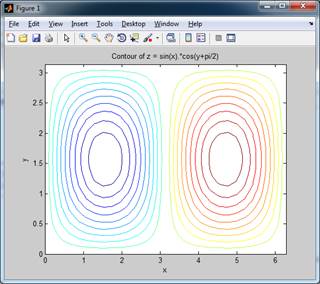
Рис. 23.
Векторные поля
Для отрисовки векторных полей используется специальная функция quiver(x,y,ux,uy,s)
Для построения этой функции необходимо задать обязательные параметры: матрицы x, y, ux, uy.
x, y - матрицы координат сетки, ux, uy - компоненты векторного поля
Необязательный параметр s - масштаб выводимых векторов
[X,Y] = meshgrid(-2:.2:2);
Z = X.*exp(-X.^2 - Y.^2);
[DX,DY] = gradient(Z,.2,.2);
contour(X,Y,Z)
hold on
quiver(X,Y,DX,DY)
colormap hsv
grid off
hold off

Рис. 23.
contour – изображение линий уровня для трехмерной поверхности
[X,Y] = meshgrid(-2:.2:2,-2:.2:3);
Z = X.*exp(-X.^2-Y.^2);
[C,h] = contour(X,Y,Z);
clabel(C,h) % маркировка линий уровня
colormap cool

Рис. 24.
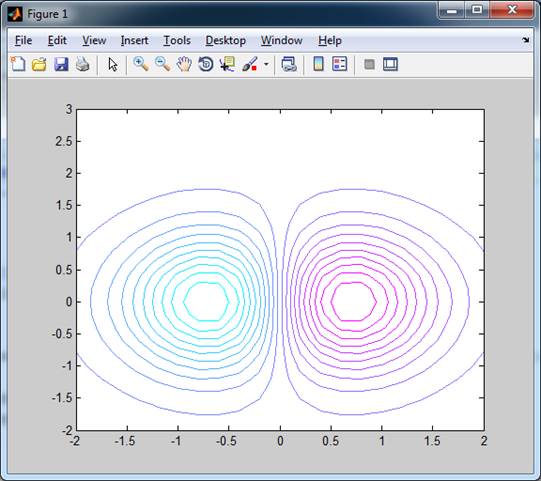
Рис. 25. contour(X,Y,Z,20) % 20 – количество линий уровня
Фигуры Лиссажу
a1=1.2; a2=1.0;w1=1.1;w2=1.0;
t=0:0.1:125;
x=a1*cos(w1*t);
y=a2*cos(w2*t);
plot(x,y);
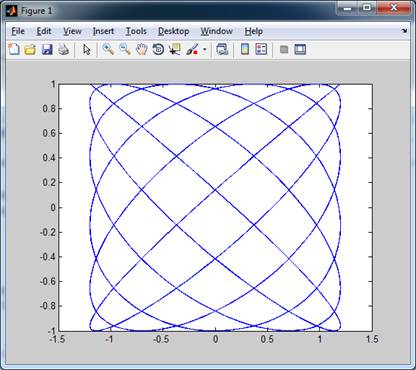
Рис. 26.
stem -дискретные графики
y = linspace(0,2*pi,10);
h = stem(cos(y),'fill','-.');
set(h,'Color','r','LineWidth',2) % Set line properties
axis ([0 11 -1 1])

Рис 27.
Круговая диаграмма (рис. 28). Она формируется функцией: pie(x). Расчет секторов диаграммы осуществляется путем сложения всех элементов вектора x и вычисление процента занимаемого элемента от этой суммы.
x = [1 3 0.5 2.5 2];
explode = [0 1 0 0 0];
pie(x, explode)
colormap jet

Рис. 28. Круговая диаграмма
Создание анимации
clear all % Очистка
t=0:0.1:100; x=0:0.3:30;
k=1.3;w=0.9;n=length(t);
y=cos(k*x-w*t(1))+cos(x-t(1));
h=line(x,y); set(h,'color','r');%Создание линии и ее свойства
axis([0 30 -3 3]); grid on
set(h,'EraseMode','xor');
pause;
for i=2:n;
y=cos(k*x-w*t(i))+cos(x-t(i));
pause(0.01);
set(h,'XData',x,'YData',y);
drawnow
end;

Рис. 29.
| Таблица 1 Функции для построения графиков | |
| Функция и ее синтаксис | Описание |
| plot(x1, y1, s1… xn, yn, sn) | Функция строит график функций y1… yn на их соответственно областях определения x1… xn и используя маркеры оформления s1… sn (они могут отсутствовать) Маркеры указываются как строки, т.е. в апострофах (см. таблицу 2). Повторный вызов этой функции, но уже с другими параметрами приведет к перерисовки полотна. Вывод последующих функциональных зависимостей происходит с изменением цвета линий графика. |
| figure | Процедура позволяющая вызвать другое окно с новым полотном для графопостроения, старое окно с графиком сохраняется и не перерисовывается. |
| polar(fi, r) | Построения функции в полярной системе координат. |
| axis([xmin xmax ymin ymax]) | Функция для увеличения области графика. Задается массив соответствующий оставляемым параметрам осей, т.е. их минимальные и максимальные значения. |
| xlabel(sx), ylabel(sy) | Вывод подписей осей. Параметр имеет строковый тип и поэтому если передается не переменная, а сам текст напрямую, то он должен быть заключен в апострофы. |
| text(x, y, 'text') | Вывод текста в любую область окна. Задаются нижние левые координаты угла начиная с которых будет выводится текст, текст заключается в апострофы. |
| title('text') | Вывод заголовка графика. |
| grid, grid on | Функция выводит координатную сетку под и на график соответственно. |
| subplot(m, n, p) | Функция создает несколько полей для вывод графика в пределах одного окна. При этом: m – сколько полей по вертикале; n – по горизонтали; p – номер поля где будет выводится график. После указания этой функции следует указание функции с помощью которой происходит построение графика. |
| hold on | Происходит «удержание графика» для вывода на его поверхность еще одного графика без перерисовки, но с сохранением цветов линий, если иного не оговорено. |
Вернемся к маркерам оформления. Они используются для придания графика большей наглядности и выразительности. При передачи стиль имеет три параметра, которые отвечают за тип линии, ее цвет и изображение точки на графике. Любой из приведенных параметров может отсутствовать, из-за этого каждый маркер имеет свой тип обозначения и расценивается средой как один символ (хотя их может быть два). При отсутствии какого-либо маркера среда считает его заданным по умолчанию. Для типа линии это сплошная; цвет – голубой, фиолетовый и т.п. (по порядку в таблице); точку система никак не выделяет.
| Таблица 2 Типы маркеров | |
| Маркер типа линии | |
| Маркер | Тип линии |
| - | Непрерывная |
| -- | Штриховая |
| : | Пунктирная (точками) |
| -. | Штрихпунктирная |
| Маркер цвета графика | |
| Маркер | Цвет графика |
| c | Голубой |
| m | Фиолетовый |
| y | Желтый |
| r | Красный |
| g | Зеленый |
| b | Синий |
| w | Белый |
| k | Черный |
| Тип проставляемой точки | |
| Маркер | Тип точки |
| . | Точка |
| + | Плюс |
| * | Звездочкой |
| о | Кружком (указывается латинская буква о) |
| х | Крестиком (указывается латинская буква х) |
Порядок указания маркеров не имеет значение, но главное, что они указываются в апострофах, как строка.
Настроить график можно через основное меню фигуры. Например, выбрав все пункты меню View для графика на рис. 2 получим рис. 30.

Рис. 30
Для построения трехмерного изображения линии можно использовать функцию plot3(x,y,z), которая произведет построение кривой линии в трехмерном пространстве, при этом входные координаты имеют вид одномерных матриц (векторов) одинаковых объемов элементов. При таком построении функция строится методом сопоставления первого элемента одного массива, второму массиву и третьему и получается точка с соответствующими координатами и т.д.
Для построения поверхности необходимо подать в функция plot3 три двумерных массива одинаковой размерности:
x=0:0.1:10;
y=0:0.1:10;
[X,Y]=meshgrid(x,y);
Z=X.^6-Y.^5+3;
plot3(X,Y,Z);
grid on
Данный код производит построение поверхности изображенной на рис. 31. Как видно, график состоит из кривых, окрашенных в разные цвета.
Для построения графика в виде каркасной поверхности используют функцию mesh(X,Y,Z). Для более насыщенного окраса графика применяется функция surf(X,Y,Z), а для более естественного окраса - surfl(X,Y,Z). При этом входные параметры остаются также двумерными матрицами одинаковой размерности.
Также существует суффиксы для вышеперечисленных функций. Суффикс добавляется в конец имени функции. Суффикс с приведет к формированию самого графика и формированию под ним линий уровня. Так же сохраняет свою работы функция subplot и функции вывода подписей графика.

Рис. 31
Не нашли, что искали? Воспользуйтесь поиском: