Выражение мощности в комплексной форме

Широкое применение комплексного представления тока и напряжения в процессе анализа электрических цепей предполагает найти комплексное представление для активной, реактивной и полной мощности. На первый взгляд эта задача не должна вызывать затруднений. Достаточно в выражение для мощности подставить комплексные ток и напряжение. Посмотрим, так ли это?

Пусть заданы комплексные ток и напряжение .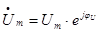

Тогда их произведение должно представлять полную мощность цепи:

Правая часть полученного выражения должна определять активную (действительную часть) и реактивную (мнимая часть) мощности. Но слагаемые правой части не соответствуют выражениям (4.16) и (4.21), так как в последних сдвиг фаз определяется разностью

Чтобы устранить такое несоответствие пользуются искусственным приемом. Под комплексным изображением полной мощности понимают произведение комплексного напряжения на комплексно-сопряженный ток. Напомним, что два комплексных числа 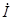и называются взаимно сопряженными, если их действительные части равны, а мнимые отличаются только знаком:

При таком определении комплексная мощность цепи определится выражением:

т.е.

(4.27)

Знак «тильда» означает комплекс полной мощности, составленный при участии сопряженного комплекса тока. Действительная часть комплексной мощности есть активная мощность, а мнимая часть - реактивная мощность. Модуль комплексного представления - полная мощность.

Рассмотрим пример. Пусть в схеме рис. (4.6) заданы ЭДС - [B] и параметры элементов: R₁=3[Ом]; R₂=2[Ом]; L=0,0095[Г]; . Определить активную, реактивную и полную мощности цепи.

Решение:

Комплекс действующего значения напряжения на входе всей схемы равен

Комплексное сопротивление цепи:

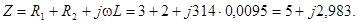
Переходим к показательной форме комплексного сопротивления. Для этого находим модуль:

и фазу:

Отсюда:

Комплекс действующего значения тока:

Сопряженный комплекс тока:

Комплекс мощности:

Отсюда:

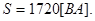
Не нашли, что искали? Воспользуйтесь поиском: