Анализ магнитных цепей постоянного тока

Суть анализа сводится к определению основных параметров магнитных цепей: магнитного потока Ф, напряженности магнитного поля Н, магнитной индукции В, сечения магнитопровода S, тока катушки I и др. При этом пользуются понятиями магнитодвижущей силы, закона полного тока, магнитного напряжения 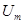и магнитного сопротивления .

Если по намагничивающей обмотке протекает ток I, то магнитодвижущей силой обмотки F называют произведение величины тока на число витков:

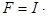v. (8.7)

Связь между магнитодвижущей силой F и напряженностью магнитного поля Н устанавливает закон полного тока:

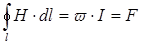(8.8)

При анализе магнитных цепей пользуются значением средней линии магнитопровода, поэтому:

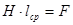. (8.9)

Выделим в магнитопроводе рис. 8.5 участок длиной «аб».

Произведение:

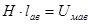(8.10)

называют магнитным напряжением.

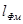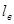Если магнитная цепь содержит два неоднородных участка длиной и , то:

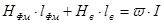
или:

. (8.11)

Таким образом алгебраическая сумма магнитных напряжений на участках цепи равна магнитодвижущей силе обмотки. Выражение (8.11) представляет собой второй закон Кирхгофа для магнитной цепи.

Аналогом первого закона Кирхгофа является теорема Гауса: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:

. (8.12)

Рассмотрим выражение для магнитного напряжения:

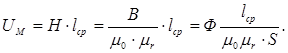
Обозначим выражение:

,

где - магнитное сопротивление.

Тогда:

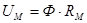. (8.13)

Равенство (8.13) представляет собой закон Ома для магнитной цепи.

Если основной характеристикой электрической цепи является вольт-амперная характеристика, то для магнитной цепи - это ампер-веберная характеристика - зависимость между магнитным потоком и намагничивающим током, т.е. (рис.8.6). Ампер – выборные характеристики часто применяют для анализа сложных магнитных цепей. На рис. 8.6 - поток в ферромагнитном материале, - поток в воздушном зазоре, _å - результирующий поток.

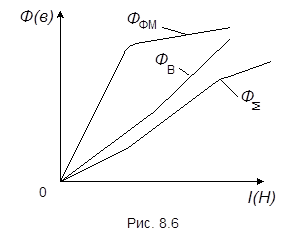Вебер-амперные характеристики адекватны гистерезисным , так как магнитный поток Ф прямопропорционален магнитной индукции (8.3), а ток намагничивающей катушки I – напряженности магнитного поля Н:

.

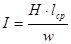Не нашли, что искали? Воспользуйтесь поиском: