Формула классической вероятности

АУДИТОРНАЯ САМОСТОЯТЕЛЬНАЯ РАБОТА №2

Если пространство элементарных событий некоторого случайного эксперимента конечно, т.е. , а все исходы (элементарные события) , 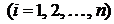— равновозможные, то вероятность появления случайного события можно определить по формуле классической вероятности

, (1)

где — множество всех исходов данного эксперимента, — множество исходов, благоприятствующих наступлению события (входящих в событие ).

Замечание

При подсчете вероятностей с помощью классического определения часто оказываются полезными сведения из комбинаторики, приведенные в предыдущей работе.

Задача 1. Монета бросается два раза. Какова вероятность того, что один раз выпадет герб, а другой раз — решетка?

Решение: Рассматриваемый эксперимент имеет четыре равновозможных исхода: . Это позволяет нам воспользоваться формулой классической вероятности (1). Наступлению интересующего нас события благоприятствуют два исхода и . Полагая в формуле , , получим .

Задача 2. На одиннадцати картонных карточках написаны буквы В Е Р О Я Т Н О С Т Ь. Случайным образом берут шесть карточек и из них составляют слово. Какова вероятность, что из букв, написанных на выбранных карточках, можно составить слово "ярость".

Решение: Пусть событие — выбранные карточки могут образовать слово "ярость". Используем для вычисления вероятности этого события формулу классической вероятности (1).

Найдем число всех исходов эксперимента, которое равно числу сочетаний из 11 (количество всех карточек) по 6 (количество выбираемых карточек):

.

Число благоприятствующих событию исходов найдем по принципу умножения, учитывая, что в заданном наборе букв буквы о и т повторяются дважды. Поэтому

.

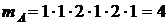Следовательно, .

Задача 3. Из колоды 36 карт наудачу вынимают три карты. Найдите вероятность того, что:

а) все три карты будут красной масти;

б) две карты будут красной масти, а одна – черной;

в) одна карта будет дама, вторая – король, а третья – валет;

г) дама, король и валет будут одной масти.

Решение:

а) Пусть событие — все три вынутые карты красной масти. По формуле классической вероятности (1)

.

Исходом эксперимента служит тройка карт, вынутая из колоды, причем нас интересует только состав этой тройки. Число всех исходов равно числу способов вынуть три карты из 36. Это неупорядоченные выборки. Следовательно, число всех исходов равно числу сочетаний из 36 по 3.

.

Поскольку карт красной масти половина, т.е. 18, то число благоприятствующих событию исходов – это число сочетаний из 18 по 3, т.е.

.

Тогда искомая вероятность равна

.

б) Пусть — событие, состоящее в том, что две вынутые карты красной масти, а одна — черная. Число различных исходов при извлечении неупорядоченной тройки карт из колоды подсчитано на предыдущем шаге и равно . Число способов вынуть две карты красной масти равно числу сочетаний из 18 по 2, а число способов вынуть одну карту черной масти равно 18. Согласно принципу умножения число благоприятных для события исходов равно

.

Тогда по формуле классической вероятности (1)

.

в) Пусть событие — вынуты дама, король и валет (масти их любые, возможно и одинаковые). Число всех исходов, как и в предыдущих случаях, равно . Число возможностей вынуть из колоды в 36 карт одну даму, или одного короля, или одного валета равно 4. Согласно принципу умножения . Тогда

.

г) Пусть событие состоит в том, что три вынутые карты — дама, король и валет одной масти. В каждой масти только одна благоприятная комбинация, а мастей — четыре. Тогда по принципу умножения благоприятных для события исходов столько же, сколько мастей в колоде карт, т.е. . Поэтому

.

Задача 4. Группа из восьми студентов с разными именами рассаживается на скамье, установленной с одной стороны прямоугольного стола. Какова вероятность того, что Маша и Саша окажутся сидящими рядом?

Решение: Обозначим событие, вероятность которого нужно подсчитать, через . Число всех возможных исходов эксперимента равно числу упорядоченных выборок из восьми элементов по восемь, т.е. числу перестановок из восьми студентов:

.

Разобьем подсчет числа благоприятных исходов на несколько простых шагов и воспользуемся принципом умножения. Обозначим белым кружком пару Маша+Саша, а каждого из оставшихся шести студентов — черным кружком и воспользуемся схемой, приведенной на рис. 1. Из рисунка видно, что наша пара может занять место среди шести студентов семью различными способами (действие первое). В самой паре Маша и Саша могут сесть , т.е. двумя способами (действие второе). Кроме того, для остальных шести студентов есть возможностей разместиться за столом при фиксированном положении пары (действие третье).

Рис. 1

Следовательно, по принципу умножения число благоприятных исходов равно произведению этих трех чисел, т.е.

.

Тогда по формуле классической вероятности (1) вероятность события равна:

.

Решение задач 1 —4 показаны на рис. 2. Здесь описана с помощью оператора присваивания функция — вероятность интересующего события, вычисляемая по формуле классической вероятности (1), а затем проводится обращение к этой функции с заданными явно или присвоенными значениями параметров и .

Задача 5. Ребенок играет с шестью буквами азбуки К, А, А, Е, Р, Т. Какова вероятность, что он случайно сложит слово РАКЕТА? Слово РАК?

Ответ: 1) ; 2) .

Задача 6. Туристическая группа из пятнадцати человек заселяется в гостиницу, где есть один четырехместный, три трехместных и один двухместный номер. Какова вероятность, что два определенных человека окажутся в двухместном номере?

Ответ: .

Рис. 2

Решение задач 5 и 6 показаны на рис. 3. Последовательность вычислений проводится так же, как и в предыдущих задачах, решение которых дано на рис. 2.

Рис. 3

Не нашли, что искали? Воспользуйтесь поиском: