Частотный коэффициент передачи, спектральный метод анализа линейных цепей

Свойства линейных четырехполюсников достаточно полно определяются частотным коэффициентом передачи (или сокращенно коэффициентом передачи)

. (1.17)

Модуль коэффициента передачи 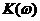называется амплитудно-частотной характеристикой (АЧХ) четырехполюсника, аргумент 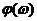– фазо-частотной характеристикой (ФЧХ) четырехполюсника.

а)
б)

Рис. 1.4. Примерный вид характеристик четырехполюсника: а – амплитудно-частотная характеристика; б – фазо-частотная характеристика

Примерный вид характеристик показан на рис. 1.4. На рис. 1.4,а показана полоса пропускания П_0,7 – область частот, в пределах которой нормированная амплитудно-частотная характеристика К_н = К/К_max принимает значения больше 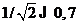. На рис..14,б показана ФЧХ, изменяющаяся в интервале от до .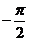

Очевидно, что частотная характеристика линейного четырехполюсника 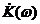не зависит от вида функции воздействия на цепь, то есть от вида входного сигнала, и полностью определяется свойствами самой цепи. Следовательно, для аналитического определения коэффициента передачи можно взять такое простое воздействие, при котором из выражения (1.15) находим коэффициент передачи. Таким воздействием может быть гармоническая функция единичной амплитуды:

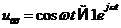. (1.18)

Тогда

. (1.19)

Подставляя (1.18) и (1.19) в (1.15), получаем

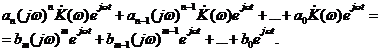
Из последнего выражения находим

. (1.20)

Таким образом, если составлено дифференциальное уравнение (1.15) для линейного четырехполюсника, то коэффициент передачи находится из выражения (1.20).

Пример: найти коэффициент передачи для четырехполюсника, изображенного на рис. 1.3,б.

Решение. Для этого четырехполюсника дифференциальное уравнение представлено выражением (1.14). Используя (1.20), находим

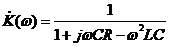. (1.21)

Этот же результат можно получить на основании определения коэффициента передачи:

.

Пусть на вход четырехполюсника поступает периодический сигнал, спектр которого есть сумма бесконечного числа амплитудно-фазовых гармоник:

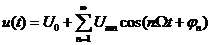, (1.22)

где U₀ – постоянная составляющая входного сигнала

;

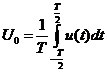U_mn – амплитуда n-ой гармоники

,

,

,

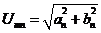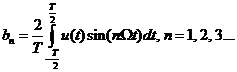– начальная фаза n-ой гармоники

;

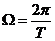, Т – период повторения входного сигнала.

Спектр периодического сигнала (1.22) получен путем преобразования ряда Фурье функции u(t), изменяющейся на интервале , где a_n b_n – коэффициенты Фурье.

Применяя принцип суперпозиции к линейному четырехполюснику, получаем сигнал на его выходе

. (1.23)

Так как коэффициент передачи имеет комплексный характер, то спектр сигнала удобно представлять в комплексной форме записи:

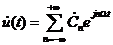, (1.24)

где 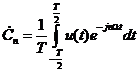. (1.25)

Выражение (1.24) получается из (1.22) применением формулы Эйлера к функции .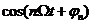

В выражении (1.24) 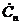есть спектральная составляющая и, как следует из (1.25), зависит только от частоты. . Если в общем случае полагать, что имеет место произвольный сигнал на входе четырехполюсника, в том числе с периодом повторения 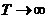, то сумма в (1.24) выродится в интеграл, а выражение (1.24) примет вид:

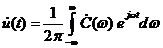, (1.26)

где 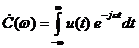. (1.27)

Заметим, что множитель 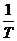в выражении (1.25) следует поставить перед суммой в выражении (1.24), которая вырождается в интеграл. Так как , то умножив и разделив на , получаем 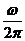. Переменная интегрирования 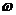уйдет под знак дифференциала, а перед интегралом в выражении (1.26) будет множитель .

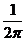Спектральные составляющие выходного сигнала определяются выражением

. (1.28)

Тогда сигнал на выходе

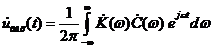. (1.29)

Выражение (1.27) носит название прямое преобразование Фурье, а выражение (1.29) – обратное преобразование Фурье.

Не нашли, что искали? Воспользуйтесь поиском: