Примеры решения задач. • Сила F,действующая на заряд Q, движущийся со скоростью vв магнитном поле с индукцией В(сила Лоренца)

Основные формулы

• Сила F, действующая на заряд Q, движущийся со скоростью v в магнитном поле с индукцией В (сила Лоренца), выражается фор­мулой

F= Q [ v B ] или F=|Q|uB sina,

где a — угол, образованный вектором скорости v движущейся ча­стицы и вектором В индукции магнитного поля.

Примеры решения задач

Пример 1. Электрон, пройдя ускоряющую разность потенциа­лов U =400 В, попал в однородное магнитное поле с индукцией B =1,5 мТл. Определить: 1)радиус R кривизны траектории; 2)ча­стоту п вращения электрона вмагнитном поле. Вектор скорости электрона перпендикулярен линиям индукции.

Решение. 1. Радиус кривизны траектории электрона опре­делим, исходя из следующих соображений: на движущийся в маг­нитном поле электрон действует сила Лоренца F. (Действием силы тяжести можно пренебречь.) Вектор силы Лоренца перпендикуля­рен вектору скорости и, следовательно, по второму закону Ньютона, сообщает электрону нормальное ускорение а_n : F=ma_n. Подставив сюда выражения F и а_n, получим

| e | uB sin a=mu²/R, (1)

где е, u, т — заряд, скорость, масса электрона; В — индукция маг­нитного поля; R — радиус кривизны траектории; a — угол между направлениями векторов скорости v и индукции В (в нашем случае v ^ B и a = 90°, sin a =l).

Из формулы (1) найдем

(2)

Входящий в выражение (2) импульс mu выразим через кинетическую энергию Т электрона:

(3)

Но кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U, определяется равенством Т= | e | U. Подставив это выражение Т в формулу (3), получим

Тогда выражение (2) для радиуса кривизны приобретает вид

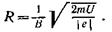
Убедимся в том, что правая часть этого равенства дает единицу длины (м):

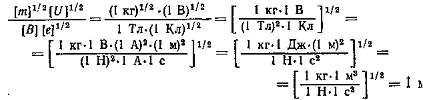
После вычисления по формуле (4) найдем

R =45 мм.

2. Для определения частоты вращения воспользуемся формулой связывающей частоту со скоростью и радиусом кривизны траектории,

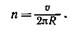
Подставив R из выражения (2) в эту формулу, получим

Произведя вычисления, найдем n =4,20 × 10⁷ c^-1 .

Пример 2. Электрон, имея скорость u =2 Мм/с, влетел воднородное магнитное поле с индукцией В =30 мТл под углом a=30° к направлению линий индукции. Определить радиус R и шаг h винтовой линии, покоторой будет двигаться электрон.

Решение. Известно, что на заряженную частицу, влетевшую в магнитное поле, действует сила Лоренца, перпендикулярная векторам магнитной индукции В и скорости v частицы:

F=QuB sin a, (1)

где Q — заряд частицы.

В случае, если частицей является электрон, формулу (1) можно записать в виде

F= |e| uB sin a.

Так как вектор силы Лоренца перпендикулярен вектору скоро­сти, то модуль скорости не будет изменяться под действием этой силы. Но при постоянной скорости, как это следует из формулы (1), останется постоянным и значение силы Лоренца. Из механики известно, что постоянная си­ла, перпендикулярная скоро­сти, вызывает движение по окружности. Следовательно, электрон, влетевший в маг­нитное поле, будет двигаться по окружности в плоскости, перпендикулярной линиям индукции, со скоростью, рав­ной поперечной составляю­щей u ₁ скорости (рис. 23.1); одновременно он будет дви­гаться и вдоль поля со ско­ростью u _||:

u _|| = u sin a, u _|| = u cos a.

В результате одновременного участия в движениях по окружно­сти и по прямой электрон будет двигаться по винтовой линии.

Радиус окружности, по которой движется электрон, найдем сле­дующим образом. Сила Лоренца F сообщает электрону нормальное ускорение а_п. По второму закону Ньютона, F=ma_n, где F= | e | u ₁ B и a_n=u ² ^ R,. Тогда

| e | u ^ B = mu₂²/R,

откуда после сокращения на u _z находим радиус винтовой линии:

Подставив значения величин т, u, e, В и a и произведя вычисле­ния, получим

R =0,19 мм.

Шаг винтовой линии равен пути, пройденному электроном вдоль поля со скоростью u _x за время, которое понадобится электрону для того, чтобы совершить один оборот,

h = u _|| T (2)

где T=2pR/u _^ — период вращения электрона. Подставив это выра­жение для Т в формулу (2), найдем

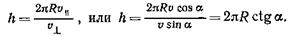
Подставив в эту формулу значения величин p, R и a и вычислив, получим

h =2,06 мм.

Пример 3. Электрон движется воднородном магнитном поле с индукцией В=0,03 Тл поокружности радиусом r=10см. Опреде­лить скорость u электрона.

Решение. Движение электрона по окружности в однородном магнитном поле совершается под действием силы Лоренца (см. примеры 1 и 2). Поэтому можно написать

(1)

откуда найдем импульс электрона:

р=тu= | е | Вr. (2)

Релятивистский импульс выражается формулой

Выполнив преобразования, получим следующую формулу для определения скорости частицы:

(3)

В данном случае р= | e | Br. Следовательно,

В числитель и знаменатель формулы (4) входит выражение |е| В_r(т ₀ с). Вычислим его отдельно:

|е| В_r / (m ₀c) = 1,76.

Подставив найденное значение отношения |е| В_r(т ₀ с) в формулу (4), получим

b = 0,871, или u = с b= 2,61-10⁸ м/с.

Электрон, обладающий такой скоростью, является релятивистским (см. § 5).

Пример 4. Альфа-частица прошла ускоряющую разность потенциалов U =104 В и влетела в скрещенные под прямым углом электрическое (E =10 кВ/м) и магнитное (B =0,1 Тл) поля. Найти отношение заряда альфа-частицы к ее массе, если, двигаясь перпендикулярно обоим полям, частица не испытывает отклонений от прямолинейной траектории.

Решение. Для того чтобы найти отношение заряда Q альфа-частицы к ее массе m, воспользуемся связью между работой сил электрического поля и изменением кинетической энергии частиц:

QU = mu ²/2,

откуда

Q/m=u²/(2U). (1)

Скорость u альфа-частицы найдем из следующих соображений. В скрещенных электрическом и магнитном полях на движущуюся заряженную частицу действуют две силы:

а) сила Лоренца F _л=Q[ vВ ], направленная перпендикулярно скорости v и вектору магнитной индукции В;

б) кулоновская сила F_K =Q E, сонаправленная с вектором напряженности Е электростатического поля (Q >0).

Сделаем рисунок с изображением координатных осей и векторных

величин. Направим вектор магнитной индукции В вдоль оси О_z (рис. 23.2), скорость v—в положительном направлении оси Ох, тогда F _л и F _k будут направлены так, как это указано на ри­сунке.

Альфа-частица не будет испытывать отклонения, если геометри­ческая сумма сил F _л+ F_k будет равна нулю. В проекции на ось

Рис. 23.2

Оу получим следующее равенство (при этом учтено, что вектор ско­рости v перпендикулярен вектору магнитной индукции В и Sin (v ^Ù B)=l):

QE—QuB = O,

откуда

u =E/B.

Подставив это выражение скорости в формулу (1), получим

Q/m=E²(2UB²).

Убедимся в том, что правая часть равенства дает единицу отно­шения заряда к массе (Кл/кг):

Произведем вычисления:

Задачи

Сила Лоренца

23.1. Определить силу Лоренца F, действующую на электрон, влетевший со скоростью u=4 Мм/с в однородное магнитное поле под углом a=30° к линиям индукции. Магнитная индукция В поля равна 0,2 Тл.

23.2. Вычислить радиус R дуги окружности, которую описывает протон в магнитном поле с индукцией В=15 мТл, если скорость u протона равна 2 Мм/с.

23.3. Двукратно ионизированный атом гелия (a-частица) дви­жется в однородном магнитном поле напряженностью H=100 кА/м по окружности радиусом R=\ 0 см. Найти скорость u a -частицы.

23.4. Ион, несущий один элементарный заряд, движется в одно­родном магнитном поле с индукцией B =0,015 Тл по окружности радиусом R=\ 0 см. Определить импульс р иона.

23.5. Частица, несущая один элементарный заряд, влетела в од­нородное магнитное поле с индукцией B =0,5 Тл. Определить момент импульса L, которым обладала частица при движении в магнитном поле, если ее траектория представляла дугу окружности радиусом R =0,2 см.

23.6. Электрон движется в магнитном поле с индукцией B =0,02 Тл по окружности радиусом R= 1 см. Определить кинетиче­скую энергию Т электрона (в джоулях и электрон-вольтах).

23.7. Заряженная частица влетела перпендикулярно линиям ин­дукции в однородное магнитное поле, созданное в среде. В результа­те взаимодействия с веществом частица, находясь в поле, потеряла половину своей первоначальной энергии. Во сколько раз будут от­личаться радиусы кривизны R траектории начала и конца пути?

23.8. Заряженная частица, двигаясь в магнитном поле по дуге окружности радиусом R ₁ =2 см, прошла через свинцовую пластину, расположенную на пути частицы. Вследствие потери энергии части­цей радиус кривизны траектории изменился и стал равным R ₂ =\ см. Определить относительное изменение энергии частицы.

23.9. Протон, прошедший ускоряющую разность потенциалов U =600 В, влетел в однородное магнитное поле с индукцией B =0,3 Тл и начал двигаться по окружности. Вычислить ее радиус R..

23.10. Заряженная частица, обладающая скоростью u=2× 10⁶ м/с, влетела в однородное магнитное поле с индукцией B =0,52 Тл. Най­ти отношение Q/m заряда частицы к ее массе, если частица в поле описала дугу окружности радиусом R =4 см. По этому отношению определить, какая это частица.

23.11. Заряженная частица, прошедшая ускоряющую разность потенциалов U=2 кВ, движется в однородном магнитном поле с ин­дукцией B =15,1 мТл по окружности радиусом R= l см. Определить отношение \е\/ m заряда частицы к ее массе и скорость u частицы.

23.12. Заряженная частица с энергией T = 1 кэВ движется в одно­родном магнитном поле по окружности радиусом R= l мм. Найти силу F, действующую на частицу со стороны поля.

23.13. Электрон движется в однородном магнитном поле с индук­цией B =0,1 Тл перпендикулярно линиям индукции. Определить силу F, действующую на электрон со стороны поля, если радиус R кривизны траектории равен 0,5 см.

23.14. Электрон движется в однородном магнитном поле напря­женностью H=4 кА/м со скоростью u=10 Мм/с. Вектор скорости направлен перпендикулярно линиям напряженности. Найти силу F, с которой поле действует на электрон, и радиус R окружности, по которой он движется.

23.15. Протон с кинетической энергией Т=1 МэВ влетел водно-родное магнитное поле перпендикулярно линиям индукции (B =1 Тл). Какова должна быть минимальная протяженность l поля в направлении, по которому летел протон, когда он находился вне поля, чтобы оно изменило направление движения протона на проти­воположное?

23.16. Электрон движется по окружности в однородном магнит­ном поле напряженностью H =10 кА/м. Вычислить период Т враще­ния электрона.

23.17. Определить частоту п вращения электрона по круговой орбите в магнитном поле, индукция В которого равна 0,2 Тл.

23.18. Электрон в однородном магнитном поле с индукцией B =0,1 Тл движется по окружности. Найти силу I эквивалентного кругового тока, создаваемого движением электрона.

23.19. Электрон, влетев в однородное магнитное поле с индук­цией B =0,2 Тл, стал двигаться по окружности радиусом R =5 см. Определить магнитный момент р _m эквивалентного кругового тока.

23.20. Два однозарядных иона, пройдя одинаковую ускоряющую разность потенциалов, влетели в однородное магнитное поле пер­пендикулярно линиям индукции. Один ион, масса т ₁ которого равна 12 а. е. м. *, описал дугу окружности радиусом R ₁ =4 см. Опреде­лить массу m ₂ другого иона, который описал дугу окружности радиу­сом R ₂ =6 см.

__________________________________{______________________}

*А. е. м.— обозначение атомной единицы массы

23.21. Два иона, имеющие одинаковый заряд, но различные мас­сы, влетели в однородное магнитное поле. Первый ион начал дви­гаться по окружности радиусом R ₁=5 см, второй ион — по окружности радиусом R ₂ =2,5 см. Найти отношение m ₁/ m ₂ масс ионов, если они прошли одинаковую ускоряющую разность потенциалов.

23.22. В однородном магнитном поле с индукцией В =100 мкТл движется электрон по винтовой линии. Определить скорость u электрона, если шаг h винтовой линии равен 20 см, а радиус R =5 см.

23.23. Электрон движется в однородном магнитном поле с индук­цией В =9 мТл по винтовой линии, радиус R которой равен 1 см и шаг h =7,8 см. Определить период Т обращения электрона и его скорость u.

23.24. В однородном магнитном поле с индукцией В =2 Тл дви­жется протон. Траектория его движения представляет собой винто­вую линию с радиусом R =10 см и шагом h =60 см. Определить кине­тическую энергию Т протона.

23.25. Электрон влетает в однородное магнитное поле напря­женностью H =16 кА/м со скоростью u=8 Мм/с. Вектор скорости составляет угол a =60° с направлением линий индукции. Определить радиус R и шаг h винтовой линии, по которой будет двигаться электрон в магнитном поле. Определить также шаг винтовой линии для электрона, летящего под малым углом к линиям индукции.

23.26. Определить энергию e, которую приобретает протон, сде­лав N =40 оборотов в магнитном поле циклотрона, если максималь­ное значение U _max переменной разности потенциалов между дуантами равно 60 кВ. Определить также относительное увеличение D m / m ₀ массы протона в сравнении с массой покоя, а также скорость v про­тона.

23.27. Вычислить скорость v и кинетическую энергию Т a-частиц, выходящих из циклотрона, если, подходя к выходному окну, ионы движутся по окружности радиусом R =50 см. Индукция В магнит­ного поля циклотрона равна 1,7 Тл.

23.28. Индукция В магнитного поля циклотрона равна 1 Тл. Какова частота n ускоряющего поля между дуантами, если в цикло­троне ускоряются дейтоны?

23.29. В циклотроне требуется ускорять ионы гелия (Не⁺⁺). Частота n переменной разности потенциалов, приложенной к дуантам, равна 10 МГц. Какова должна быть индукция В магнитного поля, чтобы период Т обращения ионов совпадал с периодом измене­ния разности потенциалов?

23.30. Определить число N оборотов, которые должен сделать протон в магнитном поле циклотрона, чтобы приобрести кинетиче­скую энергию T =10МэВ, если при каждом обороте протон проходит между дуантами разность потенциалов U =30 кВ.

23.31. Электрон движется по окружности в однородном магнит­ном поле со скоростью u=0,8 с (с — скорость света в вакууме). Маг­нитная индукция В поля равна 0,01 Тл. Определить радиус окруж­ности в двух случаях: 1) не учитывая увеличение массы со скоростью; 2) учитывая это увеличение.

23.32. Электрон движется в магнитном поле по окружности ра­диусом R=2 см. Магнитная индукция В поля равна 0,1 Тл. Опреде­лить кинетическую энергию Т электрона *.

______________

*При решении задач 23.32—23.35 учесть изменение массы частицы от ее скорости.

23.33. Электрон, влетевший в камеру Вильсона, оставил след в виде дуги окружности радиусом R =10 см. Камера находится в однородном магнитном поле с индукцией В= 10 Тл. Определить кинетическую энергию Т электрона *.

23.34. Кинетическая энергия Т a-частицы равна 500 МэВ. Части­ца движется в однородном магнитном поле по окружности радиусом R =80 см. Определить магнитную индукцию В поля *.

23.35. Электрон, имеющий кинетическую энергию Т =1,5 МэВ, движется в однородном магнитном поле по окружности. Магнитная индукция В поля равна 0,02 Тл. Определить период t обращения *.

Движение заряженных частиц в совместных магнитном и электрическом полях

23.36. Перпендикулярно магнитному полю с индукцией В =0,1 Тл возбуждено электрическое поле напряженностью Е = 100 кВ/м. Перпендикулярно обоим полям движется, не отклоняясь от прямолинейной траектории, заряженная частица. Вычислить скорость u частицы.

23.37. Заряженная частица, двигаясь перпендикулярно скрещен­ным под прямым углом электрическому (E =400 кВ/м) и магнитному (В=0,25 Тл) полям, не испытывает отклонения при определенной скорости u. Определить эту скорость и возможные отклонения D u от нее, если значения электрического и магнитного полей могут быть обеспечены с точностью, не превышающей 0,2 %.

23.38. Протон, пройдя ускоряющую разность потенциалов U =800 В, влетает в однородные, скрещенные под прямым углом маг­нитное (В=50 мТл) и электрическое поля. Определить напряжен­ность Е электрического поля, если протон движется в скрещенных полях прямолинейно.

23.39. Заряженная частица движется по окружности радиусом R =1 см в однородном магнитном поле с индукцией В =0,1 Тл. Па­раллельно магнитному полю возбуждено электрическое поле напря­женностью E =100 В/м. Вычислить промежуток времени D t, в те­чение которого должно действовать электрическое поле, для того чтобы кинетическая энергия частицы возросла вдвое.

23.40. Протон влетает со скоростью u=100 км/с в область про­странства, где имеются электрическое (E =210 В/м) и магнитное (В =3,3 мТл) поля. Напряженность Е электрического поля и маг­нитная индукция В совпадают по направлению. Определить ускоре­ние протона для начального момента движения в поле, если направ­ление вектора его скорости u: 1) совпадает с общим направлением векторов Е и В; 2) перпендикулярно этому направлению.

Не нашли, что искали? Воспользуйтесь поиском: