
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Существуют ли пределы познания?
Объяснение всего — даже в ограниченном смысле понимания всех сторон взаимодействий и элементарных составляющих Вселенной — есть одна из величайших задач, с которыми когда-либо сталкивалась наука. И теория струн впервые дает нам достаточно глубокий подход для решения этой задачи. Но сможем ли мы когда-нибудь понять все, на что способна теория, и, например, вычислить массы кварков или константу связи электромагнитного взаимодействия, от точных значений которых так много зависит во Вселенной? Как говорилось выше, на пути к цели стоят многочисленные теоретические преграды; сегодня важнее всего построить законченную формулировку теории струн/М-теории, не опирающуюся на теорию возмущений.
Но может ли случиться так, что даже при полном понимании теории струн/М-теории в рамках новой и более прозрачной формулировки квантовой механики мы окажемся неспособными ответить на вопрос о вычислении масс частиц и констант взаимодействия? Возможно ли, что вместо теоретических вычислений нам опять придется прибегнуть к экспериментальным измерениям для определения этих значений? И, более того, может ли так статься, что причиной этому будет не то, что требуется еще более глубокая теория, а то, что объяснений этим наблюдаемым свойствам реального мира не существует?
На все эти вопросы можно сразу ответить «да». Как в свое время сказал Эйнштейн: «Наиболее необъяснимое во Вселенной — это то, что она объяснима»7).
Удивление нашей способностью понимания Вселенной в целом легко улетучивается в век быстрого и впечатляющего прогресса.
248 Часть V. Единая теория в XXI веке
Возможно, однако, что существует предел познания. И существование этого предела мы будем вынуждены признать после того, как достигнем самого глубокого уровня понимания, который может предложить наука, а некоторые черты Вселенной все же останутся необъясненными. Может быть, нам придется принять, что определенные черты Вселенной таковы, каковы они есть, лишь вследствие стечения обстоятельств, случая или божественного предопределения. Успех научного подхода в прошлом дал нам смелость думать, что, обладая достаточным количеством времени и прилагая достаточные усилия, мы сможем раскрыть загадки природы. Однако столкновение с абсолютным пределом научных объяснений, а не с техническим препятствием или с текущими границами человеческого понимания, которые постепенно расширяются, будет шоком, к которому опыт прошлого не может нас подготовить.
Несмотря на то, что эта проблема непосредственно относится к поискам окончательной теории, разрешить ее мы все еще не в силах; на самом деле, проблема предела научного познания (в приведенном выше широком смысле), возможно, не будет разрешена никогда. Мы видели, например, что даже для гипотезы мульти-вселенной, ограничивающей, на первый взгляд, возможность научного познания, существуют столь же гипотетические теории, в которых возможность познания восстанавливается (по крайней мере, в принципе).
Один из основных вопросов, возникающих при таком анализе — вопрос о роли космологии в установлении проявлений единой теории. Как мы обсуждали, суперструнная космология — это молодая наука, даже по стандартам молодой теории струн. Она, без сомнения, будет объектом пристального внимания исследователей в течение ближайших лет и, вероятно, станет одной из наиболее быстро развивающихся областей теории. По мере того, как мы продолжаем получать новые сведения о свойствах теории струн/М-теории, наша способность оценивать космологические проявления этой впечатляющей попытки построения единой теории станет даже сильнее. Возможно, конечно, что такие исследования однажды убедят нас в том, что предел научному познанию действительно существует. Но возможно и обратное: что они возвестят о новой эре, в которой фундаментальное объяснение Вселенной будет, наконец, найдено.
Достичь звезд
Хотя технологические ограничения привязывают нас к Земле и ее ближайшим спутникам в Солнечной системе, способность мыслить и экспериментировать позволила нам прощупать дальние зоны внутреннего и внешнего космического пространства. За последние сто лет коллективными усилиями многих физиков были раскрыты некоторые из самых глубочайших тайн природы. И эти добытые драгоценные крупицы познания расширили границы мира, который мы считали известным, но великолепие которого мы не могли себе и близко вообразить. Один из критериев глубины физической теории — это степень, в которой она изменяет наше мировоззрение в отношении тех понятий, которые до этого считались незыблемыми. В соответствии с этим критерием, квантовая механика и теория относительности находятся за гранью самых безумных ожиданий. Волновые функции, вероятности, квантовое туннелирование, беспорядочные флуктуации вакуумной энергии, перемешивание пространства и времени, относительность одновременности, искривление пространства, черные дыры, Большой взрыв. Кто мог предположить, что интуитивный, механистический, раз и навсегда заведенный мир Ньютона окажется жалким частным случаем, и что существует целый мир, лежащий прямо за порогом мира обычных вещей?
Но даже эти потрясающие основы открытия — лишь элементы всеобъемлющей схемы. С твердой верой, что законы большого и малого должны сливаться вместе в согласованное целое, физики упорно охотятся за ускользающей единой теорией. Поиск не завершен, но благодаря теории суперструн, обобщенной до М-теории, возникла, в конце концов, убедительная схема для объединения квантовой теории, об-
Глава 15. Перспективы 249
шей теории относительности, а также теорий сильного, слабого и электромагнитного взаимодействий. Изменения наших взглядов на мир, порожденные этими достижениями, фундаментальны: мы представляем себе струнные петли и вибрирующие капли, которые увлекают все элементы мироздания в танец колеблющихся мод, педантично исполняемый во Вселенной с многочисленными скрытыми измерениями, способными претерпевать экстремальные изгибы, при которых структура пространства-времени рвется и затем снова себя восстанавливает. Кто мог подумать, что слияние гравитации и квантовой механики в единую теорию материи и взаимодействий приведет к такой революции в нашем понимании устройства Вселенной?
Без сомнения, поиск законченного и удобного вычислительного формализма теории суперструн сулит еще более грандиозные сюрпризы. Уже сейчас в исследованиях по М-теории мы увидели скрывающуюся за планковской длиной новую область Вселенной, в которой, возможно, нет понятия пространства и времени. И вот противоположная крайность: мы видели, что наша Вселенная может оказаться всего лишь одним из неисчислимых пузырей пены на поверхности широкого и турбулентного космического океана мульти-вселенной. Эти рассуждения сейчас кажутся невероятными, но они могут предвещать следующий скачок в нашем понимании Вселенной.
И в то время как наши взоры обращены в будущее в предвкушении грядущих чудес, мы можем оглянуться назад и изумиться проделанному пути. Поиск фундаментальных законов Вселенной — это определенно человеческая драма, которая укрепила разум и обогатила дух людей. Вот яркое описание Эйнштейна его собственного поиска смысла гравитации: «Годы беспокойного поиска во тьме с огромной жаждой результата, чередованием уверенности и опустошения, и, наконец, прорывом к свету»8'. Без сомнения, эта фраза — свидетельство человеческой борьбы. Мы все, каждый по-своему, искатели истины, и мы все жаждем ответа на вопрос, зачем мы в этом мире. Взбираясь вместе на гору познания, физики следующих поколений крепко стоят на плечах предыдущих, смело устремляясь к вершине. Удастся ли кому-нибудь из наших потомков получить полную картину и увидеть обширную и элегантную Вселенную во всей ее ослепительной красе? Мы не можем этого предсказать. По мере того как каждое новое поколение взбирается немного выше, мы понимаем изречение Якоба Броновски: «В каждом веке есть поворотный момент, новый способ видения и признания согласованности мира»9). И так как наше поколение уже восхищается новым видением Вселенной — нашим новым способом признания согласованности мира, мы выполнили часть задачи, построив свою ступеньку на лестнице, ведущей человека к звездам.
Примечания
Глава 1
1. Таблица справа — расширенный вариант табл. 1.1. В нее входят массы и константы взаимодействия элементарных частиц всех трех семейств. Кварк каждого типа может обладать тремя значениями сильного заряда, которые названы (довольно причудливо) цветами. Приведенные значения константы слабого взаимодействия представляют собой, строго говоря, «третью компоненту» слабого изоспина. (Мы не привели «правосторонние» компоненты частиц — они отличаются отсутствием заряда слабого взаимодействия.)
2. Помимо показанных на рис. 1.1 петель (замкнутых струн), могут также существовать струны со свободными концами (так называемые открытые струны). Чтобы упростить изложение, в большей части книги мы ограничимся замкнутыми струнами, хотя практически все, о чем мы будем говорить, справедливо для струн обоих типов.
3. Из письма Альберта Эйнштейна к другу. Написано в 1942 г., цитируется по книге: Tony Hey, Patrick Wallers, Einstein's Mirror. Cambridge, Eng.: Cambridge University Press, 1997.
4. Steven Weinberg, Dreams of a Final Theory. New York: Pantheon, 1992, p. 52. (Рус. пер.: Вайнберг С. Мечты об окончательной теории. М: УРСС, 2004.)
5. Интервью с Эдвардом Виттеном, 11 мая 1998 г.
Глава 2
1. Присутствие массивных тел, подобных нашей Земле, усложняет картину за счет добавления гравитационных сил. Поскольку мы сфокусируем свое внимание на движении в горизонтальном, а не в вертикальном направлении, можно игнорировать присутствие Земли. В следующей главе мы подробно рассмотрим гравитацию.
2. Если выражаться более точно, 300 000 км/с — это скорость света в вакууме. Когда свет распространяется в какой-либо среде, например в воздухе или стекле, его скорость уменьшается, подобно тому, как камень, брошенный со скалы, замедляет свое движение, войдя в воду. Поскольку замедление скорости света в среде по отношению к его скорости в вакууме не оказывает никакого влияния на рассматриваемые нами релятивистские эффекты, мы будем его в дальнейшем игнорировать.
3. Для читателей, любящих математику, заметим, что эти наблюдения могут быть выражены в количественной форме. Например, если движущиеся световые часы имеют скорость и, а фотон совершает свое движение «туда и обратно» за t секунд
(по показаниям неподвижных часов), то за время, которое потребуется фотону, чтобы вернуться к нижнему зеркалу, световые часы пройдут расстояние vt. Используя теорему Пифагора, можно рассчитать длину пути по диагонали на рис. 2.3.
Она составит  , где Л представляет
, где Л представляет
собой расстояние между зеркалами световых часов (равное 15 см). Суммарная длина двух диагональных отрезков будет равна 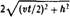 Поскольку скорость света является константой, которая обычно обозначается с, фотону потребуется
Поскольку скорость света является константой, которая обычно обозначается с, фотону потребуется  секунд на то, чтобы пройти оба диагональных отрезка. Таким образом, у нас есть уравнение
секунд на то, чтобы пройти оба диагональных отрезка. Таким образом, у нас есть уравнение  , из которо-
, из которо-
го мы можем найти значение  Чтобы избежать недоразумений, обозначим это
Чтобы избежать недоразумений, обозначим это
значение как  , индекс у t
, индекс у t
в этом выражении указывает на то, что мы измеряем продолжительность одного цикла для движущихся часов. С другой стороны, время цикла для неподвижных часов t неподв можно рассчитать по формуле  . Используя неслож-
. Используя неслож-
ные алгебраические преобразования, получим выражение  , которое непосредственно свидетельствует о том, что продолжительность тика движущихся часов больше, чем у неподвижных. Это означает, что для промежутка времени между двумя выбранными событиями движущиеся часы совершат меньшее число тиков, чем неподвижные, т. е. для движущегося наблюдателя пройдет меньше времени.
, которое непосредственно свидетельствует о том, что продолжительность тика движущихся часов больше, чем у неподвижных. Это означает, что для промежутка времени между двумя выбранными событиями движущиеся часы совершат меньшее число тиков, чем неподвижные, т. е. для движущегося наблюдателя пройдет меньше времени.
4. Если опыт с ускорителем частиц, понятный узкому кругу специалистов, не выглядит для вас очень убедительным, приведем еще один пример. В октябре 1971 г. Дж. С. Хафеле, работавший в то время в университете Вашингтона в Сент-Луисе и Ричард Китинг из Военно-морской лаборатории США провели эксперимент, в ходе которого цезиевые атомные часы провели около 40 часов на борту самолетов, совершавших коммерческие авиарейсы. После того, как был учтен ряд тонких эффектов, связанных с действием гравитации (которая будет обсуждаться в следующей главе), расчеты с использованием специальной теории относительности показали, что показания движущихся часов должны быть меньше показаний неподвижных часов на несколько сотен миллиардных долей секунды. Именно такие данные и получили Хафеле и Китинг: для движущихся часов время действительно замедляет ход.
5. Хотя на рис. 2.4 правильно изображено сжатие тела в направлении движения, этот рисунок не дает представления о том, что мы в действительности
Примечания 251
| Частица | Масса* | Электрический заряд" | Заряд слабого взаимодействия | Заряд сильного взаимодействия |
| Семейство 1 | ||||
| Электрон | 0,00054 | -1 | -1/2 | |
| Электронное нейтрино | <!0"8 | 1/2 | ||
| и -кварк | 0,0047 | 2/3 | 1/2 | красный, зеленый, синий |
| d-кварк | 0,0074 | -1/3 | -1/2 | красный, зеленый, синий |
| Семейство 2 | ||||
| Мюон | 0,11 | -1 | -1/2 | |
| Мюонное нейтрино | < 0,0003 | 1/2 | ||
| с-кварк | 1,6 | 2/3 | 1/2 | красный, зеленый, синий |
| s -кварк | 0,16 | -1/3 | -1/2 | красный, зеленый, синий |
| Семейство 3 | ||||
| Тау-частица | 1,9 | -1 | -1/2 | |
| Тау-нейтрино | < 0,033 | 1/2 | ||
| t -кварк | 189,0 | 2/3 | 1/2 | красный, зеленый, синий |
| b -кварк | 5,2 | -1/3 | -1/2 | красный, зеленый, синий |
* В единицах массы протона. ** В единицах заряда протона.
увидим, если мимо нас пролетит тело, движущееся со световой скоростью (при условии, что наш глаз или фотографическое оборудование, которое мы используем, имеют достаточную разрешающую способность, чтобы вообще хоть что-то увидеть!). Чтобы увидеть что-то, глаз или камера должны получать свет, отраженный от поверхности тела. Однако, поскольку отраженный свет приходит от разных участков тела, тот свет, который мы будем видеть в каждый момент времени, будет проходить по путям различной длины. Результатом явится релятивистская иллюзия — тело будет выглядеть сократившимся по длине и повернутым.
6. Для читателей, имеющих математическую подготовку, заметим, что по 4-вектору положения в пространстве-времени  можно построить 4-вектор скорости
можно построить 4-вектор скорости

где т — собственное время, определяемое соотношением

Тогда «скорость в пространстве-времени» будет представлять собой величину 4-вектора и,

которая равна скорости света с. Теперь уравнение

можно переписать в форме
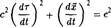
Это показывает, что увеличение скорости тела в пространстве  должно сопровождать-
должно сопровождать-
ся уменьшением величины  , которая пред-
, которая пред-
ставляет собой скорость объекта во времени (скорость, с которой идут его собственные часы  по отношению к скорости наших неподвижных часов dt).
по отношению к скорости наших неподвижных часов dt).
252 Примечания
Глава 3
1. Isaac Newton, Sir Isaac Newton's Mathematical Principle of Natural Philosophy and His System of the World, Irans. A. Motleand Florian Cajori. Berkeley: University of California Press, 1962, v. I, p. 634. (В рус. пер. см.: письмо Ньютона архиепископу Бентли от 25 февраля 1693 г. // Письма Ньютона и Ньютону. М..-ВИЕТ, 1993, №1, с. 33-45.)
2. Если говорить точнее, Эйнштейн осознал, что принцип эквивалентности сохраняется до тех пор, пока наблюдения ограничены достаточно малой областью пространства, т. е. до тех пор, пока ваше «купе» достаточно мало. Причина этого состоит в следующем. Интенсивность (и направление) гравитационных полей могут изменяться от точки к точке. Однако мы считаем, что купе в целом ускоряется как единое тело и, следовательно, это ускорение имитирует действие однородного гравитационного поля. Чем меньше будет купе, тем меньше пространство, в котором гравитационное поле может изменяться и, следовательно, тем более применимым станет принцип эквивалентности. Разность между однородным гравитационным полем, имитируемым ускорением, и возможно неоднородным «реальным» гравитационным полем, созданным совокупностью массивных тел, носит название «приливного» гравитационного поля (поскольку им объясняется влияние тяготения Луны на приливы на Земле). Подытоживая данное примечание, можно сказать, что уменьшая размер купе, можно сделать приливные гравитационные поля менее заметными и добиться того, что ускоренное движение и «реальное» гравитационное поле будут неразличимы.
3. Цитируется по книге: Albrecht Folsing, Albert Einstein. New York: Viking, 1997, p. 315.
4. John Stachel, Einstein and the Rigidly Rotating Disk. Опубликовано в General Relativity and Gravitation, ed. A. Held. New York: Plenum, 1980, p. I.
5. Анализ аттракциона Верхом на торнадо или «жесткого вращающегося диска», как он называется на более профессиональном языке, может легко привести к недоразумениям. Так, например, и по сей день нет общего согласия по ряду деталей этого примера. В тексте мы следовали духу анализа, выполненного самим Эйнштейном; в примечании мы, оставаясь на той же точке зрения, постараемся пояснить некоторые особенности, которые могут привести к недоразумениям. Во-первых, может показаться непонятным, почему длина окружности колеса не испытает лоренцевского сокращения в той же мере, что и линейка: в этом случае результат, полученный Слимом, совпадал бы с первоначальным. Здесь следует иметь в виду, что мы все время считали, что колесо непрерывно вращается и никогда не рассматривали его в состоянии покоя. Таким образом, с точки зрения неподвижных наблюдателей, единственное различие между измерениями длины окружности и измерениями Слима будет состоять в том, что линейка Слима испытала лоренцевское сокращение; колесо вращалось и во время наших измерений, и тогда, когда мы
наблюдали за измерениями Слима. Видя, что линейка Слима испытала сокращение, мы понимали, что ему придется приложить ее большее число раз, чтобы пройти по всей длине окружности и, следовательно, он получит большее значение, чем мы. Лоренцевское сокращение окружности колеса можно установить, только сравнив результаты измерений на покоящемся и вращаюшемся колесе, однако такое сравнение нас не интересовало. Во-вторых, хотя нам и не требовалось анализировать аттракцион в состоянии покоя, у вас может остаться вопрос, а что случится с колесом, когда оно замедлит свое движение и остановится? Может показаться, что в этом случае следует учитывать изменение длины окружности при изменении скорости вращения, вызванное сокращением Лоренца. Но как можно согласовать это с неизменным радиусом? Это тонкая проблема, решение которой опирается на тот факт, что в реальном мире не существует абсолютно жестких тел. Тела могут растягиваться и изгибаться в ответ на испытываемое ими растяжение или сжатие. Если этого не произойдет, то, как указал Эйнштейн, диск, изготовленный путем охлаждения вращающейся отливки, может разрушиться при изменении скорости вращения. Более подробно история с жестким вращающимся диском описана в работе Стахеля4).
6. Искушенный читатель поймет, что в примере с аттракционом Верхом на торнадо, т. е. в случае равномерно вращающейся системы отсчета, искривленные трехмерные пространственные сечения, на которых мы сконцентрировали наше внимание, объединятся в четырехмерное пространство-время с нулевой кривизной.
7. Цитата Германа Минковского взята из работы: Albrecht Folsing, Albert Einstein. New York: Viking, 1997, p. 189.
8. Интервью с Джоном Уилером, 27 января 1998 г.
9. Точность существующих атомных часов достаточна для того, чтобы обнаружить столь малые и даже еще меньшие искривления времени. Например, в 1976 г. Робер Вессо и Мартин Левин из Смитсонианской астрофизической обсерватории Гарвардского университета совместно со своими коллегами из Национального управления по аэронавтике и космическим исследованиям США (NASA) установили на ракете Scout D, стартовавшей с о, Уоллопс в штате Вирджиния, атомные часы, точность которых составляет одну триллионную долю секунды в час. Они надеялись продемонстрировать, что когда ракета достигнет достаточной высоты (в результате чего уменьшится влияние гравитационного притяжения Земли), идентичные часы, расположенные на Земле (которые будут в полной мере подвергаться действию земного тяготения) будут идти медленнее. Благодаря двустороннему обмену микроволновыми сигналами исследователи смогли сравнить показания двух атомных часов и установить, что действительно, на достигнутой ракетой максимальной высоте 10000 км установленные на ней атомные часы обогнали на 4 миллиардных доли секунды часы, оставшиеся на Земле. Расхо-
Примечания 253
ждение экспериментальных данных с результатами теоретических расчетов составило менее 0,01 %.
10. В середине XIX в. французский ученый Урбен Жан-Жозеф Леверье установил, что орбита планеты Меркурий немного отклоняется от орбиты, по которой она должна прашаться вокруг Солнца в соответствии с ньютоновским законом всемирного тяготения. В течение более чем полувека предлагались самые разные объяснения так называемой аномальной прецессии перигелия (на обычном языке, в крайних точках своей орбиты Меркурий оказывался не в том месте, в котором он должен был находиться согласно теории Ньютона). В качестве возможных причин рассматривалось гравитационное влияние неизвестной планеты или пояса астероидов, влияние неизвестного спутника, воздействие межзвездной пыли, сплюснутость Солнца, однако ни одно из этих объяснений не получило общего признания. В 1915 г. Эйнштейн рассчитал прецессию перигелия Меркурия с помощью уравнений только что открытой им общей теории относительности. Он получил результат, который по его собственному свидетельству заставил его сердце учащенно биться: значение, полученное с помощью обшей теории относительности, в точности совпадало с экспериментальными данными. Этот успех, несомненно, был одной из важных причин, заставивших Эйнштейна поверить в свою теорию, но большинство других исследователей ожидало предсказания новых явлений, а не объяснения уже известных аномалий. Более подробно эта история описана в книге: Abraham Pais. Subtle Is the Lord: The Science and the Life of Albert Einstein. New York: Oxford University Press, 1982. (Рус. пер.: Пайс А. Научная деятельность и жизнь Альберта Эйнштейна, М.: Наука, Физматлит, 1989.)
11. Robert P. Crease and Charles C.Mann, The Second Creation. New Brunswick. N. J.: Rutgers University Press, 1996, p. 39.
12. К большому удивлению ученых, недавние тщательные исследования скорости расширения Вселенной показали, что в нее может давать вклад очень небольшая, но ненулевая космологическая постоянная.
Глава 4
1. Richard Feynman, The Character of Physical Lain. Cambridge, Mass.: MIT Press, 1965, p. 129, (Рус. пер.: Феинман P. Характер физических законов. М.: Мир, 1968.)
2. Хотя работа Планка разрешила загадку бесконечной энергии, по всей видимости, не эта загадка была непосредственной причиной, побудившей его к этому исследованию. Планк пытался решить другую, очень близкую проблему, связанную с экспериментальными данными, описывающими распределение энергии в духовке (или. если быть более точным, в «черном теле») по длинам волн. Дополнительные сведения по истории этих работ интересующийся читатель может найти в книге Thomas S. Kuhn, Black-Body Theory and the Quan-
tum Discontinuity, 1894-1912. Oxford. Eng.: Clarendon, 1978.
3. Более точно, Планк показал, что волны, минимальная энергия которых превышает их ожидаемый средний энергетический вклад (согласно термодинамике девятнадцатого века), подавляются по экспоненциальному закону. Степень подавления резко увеличивается с увеличением частоты.
4. Постоянная Планка равна 1,05 х 10"2' (г-см2)/с.
5. Timothy Ferris, Coming of Age in the Milky Way. New York: Anchor, 1989, p. 286.
6. Стивен Хокинг. Доклад на Амстердамском симпозиуме по гравитации, черным дырам и теории струн, 21 июня 1997 г.
7. Следует отметить, что с помошью фейнмановского подхода к квантовой механике можно вывести подход, основанный на волновых функциях, и наоборот; следовательно, эти два подхода полностью эквивалентны. Однако концепции, терминология и интерпретация, даваемая каждым из этих подходов, различаются очень сильно, несмотря на то, что решения, которые они дают, тождественны.
8. Richard Feynman, QED: The Strange Theory of Light and Matter. Princeton: Princeton University Press, 1988. (Рус. пер.: Феинман Р. Квантовая электродинамика: странная теория света и материи. М.: Наука, 1988 (Библиотечка «Квант». Вып. 66).)
Глава 5
1. Stephen Hawking, A Brief History of Time. New York: Bantam Books, 1988, p. 175. (Рус. пер.: Хокинг С. От Большого взрыва до черных дыр. М.: Мир, 1998.)
2. Цитируется по книге: Timolhy Ferris, The Whole Shebang. New York: Simon & Schuster, 1997, p. 97.
3. Если вы все еще озабочены тем, как вообще что-либо может происходить в пустом пространстве, вы должны понять, что соотношение неопределенностей накладывает ограничения на то, насколько «пустой» может в действительности быть область в пространстве; оно изменяет наше понимание пустого пространства. Например, применительно к волновым возмущениям поля (таким, как электромагнитные волны, распространяющиеся в электромагнитном поле) соотношение неопределенностей утверждает, что амплитуда волны и скорость изменения амплитуды связаны тем же самым отношением обратной пропорциональности, которое выполняется для положения частицы и ее скорости. Чем точнее указана амплитуда, тем менее точно мы знаем скорость, с которой она изменяется. Когда мы говорим, что область в пространстве является пустой, мы обычно имеем в виду, что, помимо всего прочего, в ней не распространяются волны и что все поля имеют нулевую интенсивность. Пользуясь грубым, но очень наглядным языком, можно перефразировать данное выражение, сказав, что амплитуды всех волн, проходящих через данную область, в точности равны нулю. Однако если амплитуды точно известны, то согласно соотношению неопре-
254 Примечания
деленностей это означает, что скорость изменения амплитуды является совершенно неопределенной и может принимать любое значение. Но если амплитуда изменяется, это означает, что в следующий момент она уже не может быть нулевой, даже несмотря на то, что область пространства по-прежнему остается «пустой». Опять же, в среднем поле будет нулевым, поскольку в одних областях оно будет принимать положительные значения, а в других — отрицательные; средняя суммарная энергия области не изменится. Но это верно только в среднем. Квантовая неопределенность предполагает, что энергия поля (даже в пустой области пространства) флуктуирует от больших значений к меньшим. При этом амплитуда флуктуации увеличивается по мере уменьшения расстояний и промежутков времени, и которых исследуется эта область. Согласно формуле Е = тс2 энергия, заключенная в таких кратковременных флуктуациях, может быть преобразована в массу путем мгновенного образования пары, состоящей из частицы и соответствующей античастицы, которые затем быстро аннигилируют, чтобы сохранить средний баланс энергии.
4. Даже несмотря на то. что первоначальное уравнение Шредингера (то, в котором учитывалась специальная теория относительности) не давало точного описания квантово-механических характеристик электронов в атомах водорода, ученые вскоре поняли, что это ценный инструмент при использовании в надлежащем контексте, который и сегодня еще не вышел из употребления. Однако к тому времени, как Шредингер опубликовал свое уравнение, его опередили Оскар Клейн и Уолтер Гордон, поэтому его релятивистское уравнение носит название уравнения «Клейна—Гордона».
5. Для математически подготовленного читателя заметим, что принципы симметрии, используемые в физике элементарных частиц, обычно основаны на группах, чаще всего на группах Ли. Элементарные частицы систематизируются по представлениям различных групп; уравнения, описывающие эволюцию частиц во времени, должны удовлетворять соответствующим преобразованиям симметрии. Для сильного взаимодействия такой группой симметрии является группа SU(3) (аналог обычных трехмерных вращений, но в комплексном пространстве), при этом три цветовых заряда кварка заданного типа преобразуются по трехмерному представлению. Смещение (от красного, зеленого, синего к желтому, индиго и фиолетовому), которое упомянуто в тексте, если быть более точным, представляет собой SU(3) преобразование, примененное к «цветовым координатам» кварка. Калибровочной является симметрия, в которой групповые преобразования могут зависеть от точек пространства-времени: в этом случае «вращение» цветов кварка будет происходить по-разному в различных точках пространства и в различные моменты времени.
6. При разработке квантовых теорий трех негравитационных взаимодействий физики также столкнулись с вычислениями, которые приводили к бесконечным результатам. Однако со временем ученые осознали, что от бесконечностей можно из-
бавиться с помощью процедуры, известной как перенормировка. Бесконечности, возникающие при попытках объединить общую теорию относительности и квантовую механику, являются гораздо более серьезными, от них нельзя избавиться с помощью перенормировки. Позднее стало ясно, что бесконечные результаты сигнализируют о том, что теория используется за пределами области своей применимости. Поскольку цель исследований — «окончательная» или «последняя» теория, область применимости которой в принципе не ограничена, физики ищут теорию, в ответах которой не появлялись бы бесконечные величины, независимо от того, насколько экстремальной является анализируемая физическая система.
7. Величину планковской длины можно получить с использованием простых рассуждений, основанных на том, что физики называют размерным анализом. Идея состоит в следующем. Когда та или иная теория формулируется в виде набора уравнений, то чтобы теория приобрела связь с действительностью, абстрактным символам должны быть поставлены в соответствие физические характеристики реального мира. В частности, нужно ввести систему единиц измерения. Например, если мы обозначим некоторую длину символом а, то у нас должна быть шкала для интерпретации этого значения. В конце концов, если уравнение говорит нам, что искомая длина равна 5, мы должны знать, означает ли это 5 см, 5 км или 5 световых лет и т. п. В теории, которая включает в себя обшую теорию относительности и квантовую механику, естественный выбор единиц измерения выглядит следующим образом. В природе есть две константы, которые входят в уравнения общей теории относительности: скорость света с и ньютоновская гравитационная постоянная С Квантовая механика определяется постоянной Планка  . Исследуя единицы, в которых выражены эти константы (например, с представляет собой скорость и поэтому выражается как расстояние, деленное на время, и т.п.), можно заметить, что величина
. Исследуя единицы, в которых выражены эти константы (например, с представляет собой скорость и поэтому выражается как расстояние, деленное на время, и т.п.), можно заметить, что величина  имеет размерность длины; ее значение составляет 1,616 х 10--33 см. Это и есть планковская длина. Поскольку она содержит гравитационный и пространственно-временной параметры (G и с), а также квантово-механическую константу (
имеет размерность длины; ее значение составляет 1,616 х 10--33 см. Это и есть планковская длина. Поскольку она содержит гравитационный и пространственно-временной параметры (G и с), а также квантово-механическую константу ( ), она устанавливает шкалу для измерений (естественную единицу длины) для любой теории, которая пытается объединить обшую теорию относительности и квантовую механику. Когда мы используем в тексте выражение «планковская длина», мы часто имеем в виду приближенное значение, отличающееся от 10--33 см не более чем на несколько порядков.
), она устанавливает шкалу для измерений (естественную единицу длины) для любой теории, которая пытается объединить обшую теорию относительности и квантовую механику. Когда мы используем в тексте выражение «планковская длина», мы часто имеем в виду приближенное значение, отличающееся от 10--33 см не более чем на несколько порядков.
8. В настоящее время, помимо теории струн, активно развиваются два других подхода к объединению общей теории относительности и квантовой механики. Один из них, возглавляемый Роджером Пенроузом из Оксфордского университета, известен под названием теории твисторов. Другой подход, появление которого отчасти было инициировано работами Пенроуза, развивается Абхаем Аштекаром
Примечания 255
из университета штата Пенсильвания, и получил название метода новых переменных. Мы не будем рассматривать эти подходы в данной книге, однако появляются все более обоснованные предположения о том, что они могут иметь глубокую связь с теорией струн, и, возможно, все три подхода ведут к одному и тому же решению проблемы объединения общей теории относительности и квантовой механики.
Глава 6
1. Знающий читатель поймет, что в данной главе рассматривается только пертурбативная теория струн; выходящие за рамки теории возмущений аспекты обсуждаются в главах 12 и 13.
2. Интервью с Джоном Шварцем, 23 декабря 1997 г.
3. Схожие предположения были независимо высказаны Тамиаки Йонея, а также Коркутом Бардакчи и Мартином Гальперном. Значительный вклад в разработку теории струн на ранних этапах ее существования был также сделан шведским физиком Ларсом Бринком.
4. Интервью с Джоном Шварцем. 23 декабря 1997 г.
5. Интервью с Майклом Грином, 20 декабря 1997 г.
6. Стандартная модель предлагает механизм, дающий частицам массу, так называемый механизм Хиггса, получивший свое имя в честь шотландского физика Питера Хиггса. Однако с точки зрения объяснения значений масс частиц, задача здесь просто перекладывается на гипотетическую «частицу, дающую массу» — хиггсовский бозон. В настоящее время ведутся поиски этой частицы, но, опять же, даже если удастся обнаружить ее и определить ее свойства, они будут представлять собой входные данные для стандартной модели, не имеющие никакого теоретического объяснения.
7. Для читателей, имеющих математическую подготовку, укажем, что связь между модами колебаний струны и константами взаимодействия может быть более точно описана следующим образом. При квантовании струны ее возможные состояния, как и состояния любой квантово-механической системы, могут быть представлены векторами в гильбертовом пространстве. Эти векторы могут быть разложены по собственным значениям некоторого набора коммутирующих эрмитовых операторов. Среди этих операторов имеется гамильтониан, собственное значение которого дает энергию и, следовательно, массу этой колебательной моды, а также операторы, генерирующие различные калибровочные симметрии этой теории. Собственные значения этих последних операторов и дают константы взаимодействия, которые несут соответствующие колебательные моды струны.
8. Основываясь на догадках, сделанных в ходе второй революции в теории суперструн (обсуждаемой в главе 12), Виттен и Джо Ликкен (из Национальной лаборатории высокоэнергетических исследований) нашли маленькую, но возможную лазейку
в этом заключении. Используя ее, Ликкен предположил, что струны могут находиться под гораздо меньшим натяжением, и, следовательно, иметь гораздо больший размер, чем считалось первоначально. В действительности они могут оказаться столь большими, что могут быть обнаружены с помощью ускорителей частиц следующего поколения. Если эта маловероятная возможность окажется реальностью, открываются волнующие перспективы того, что многие замечательные следствия теории струн, обсуждаемые в этой и в последующих главах, смогут быть экспериментально проверены в течение ближайшего десятилетия. Но, как мы увидим в главе 9, даже в случае более «традиционного» сценария, разделяемого специалистами по теории струн, согласно которому струны обычно имеют длину порядка I0--33 см, остаются косвенные методы экспериментальной проверки. 9. Знающий читатель поймет, что фотон, образовавшийся при столкновении электрона и позитрона, является виртуальным и, следовательно, должен быстро высвободить свою энергию путем образования пары частица-античастица. 10. Конечно, камера работает, улавливая отражающиеся от интересующих нас объектов фотоны и регистрируя их на фотопленке. Использование камеры в этом примере является символическим, поскольку мы не представляем себе фотонов, отражающихся от сталкивающихся струн. Мы просто хотим зарегистрировать на рис. 6.7 в всю историю взаимодействия. Сказав это, мы должны обратить ваше внимание на один тонкий момент, о котором умалчивает обсуждение в основном тексте. В главе 4 мы узнали, что квантовая механика может быть сформулирована с использованием фейнмановского метода суммирования по траекториям, в котором движение объектов анализируется путем суммирования вклада всех возможных траекторий, ведущих от выбранной начальной точки к некоторой конечной (каждой траектории в методе Фейнмана сопоставляется статистический вес). На рис. 6.6 и 6.7 мы показали вклад бесконечного числа возможных траекторий, по которым точечные частицы (рис. 6.6) или струны (рис. 6.7) следуют от начальной точки к пункту назначения. Однако приводимое в разделе обсуждение в равной мере применимо и к любой другой возможной траектории, а значит и ко всему квантово-механическому процессу в целом. (Фейнмановская формулировка квантовой механики точечных частиц с использованием подхода, основанного на суммировании по траекториям, была обобщена на случай теории струн в работах Стэнли Мандельстама из университета штата Калифорния в Беркли и Александра Полякова, в настоящее время работающего на физическом факультете Принстонского университета.)
Глава 7
1. Цитируется по книге R. Clark, Einstein: The Life and Times. New York: Avon Books, 1984, p. 287.
256 Примечания
2. Если говорить более точно, спин, равный 1/2, означает, что момент импульса электрона, связанный с его спином, составляет 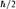
3. Открытие и развитие понятия суперсимметрии имеет непростую историю. В дополнение к тем, кто указан в тексте, основополагающий вклад внесли Р. Хааг, М. Сониус, Дж. Т. Лопушанский, Ю. А. Гольфанд, Е. П. Лихтман, Дж. Л. Шервэ, Б.Сакита, В. П. Акулов, Д. В. Волков и В. А. Сорока. Некоторые из их работ вошли в обзор Rosanne Di Stefano, Notes on the Conceptual Development of Supersymmetry. Institute for Theoretical Physics, State University of New York at Stony Brook, preprint ITP-SB-887S.
4. Для читателя, имеющего математическую подготовку, заметим, что это расширение включает дополнение обычных декартовых координат в пространстве-времени новыми, квантовыми координатами, скажем и и v, которые антикоммутируют: и х v — —v x и. Это позволяет рассматривать суперсимметрию как симметрию относительно трансляций в кванюво-механическом расширении пространства-времени.
5. Для читателя, интересующегося деталями этого технического вопроса, заметим следующее. В примечании 6 к главе 6 мы упоминали, что стандартная модель вводит «частицу, даюшую массу», хиггсовский бозон, которая генерирует измеряемые экспериментально массы элементарных частиц, перечисленных в табл. 1.1 и 1.2. Для того чтобы эта процедура работала, хиггеовская частица сама по себе не должна быть слишком тяжелой: проведенные исследования показывают, что ее масса, во всяком случае, не должна превышать примерно I 000 масс протона. Однако окаилось, что квантовые флуктуации могут вносить значительный вклад в массу хиггеовской частицы: это, в принципе, может приводить к массам, близким к планковской. Тем не менее теоретикам удалось установить, что можно избежать этого результата, указывающего на серьезный дефект стандартной модели, путем тонкой настройки некоторых параметров стандартной модели (прежде всего так называемой голой массы хиггеовской частицы) с точностью порядка 10--15. что позволяет нейтрализовать влияние квантовых флуктуации па массу хиггсовской частицы.
6. Один тонкий момент, относящийся к рис. 7.1, состоит в том, что на этом рисунке интенсивность слабого взаимодействия занимает промежуточное положение между интенсивностью сильного и электромагнитного взаимодействия, хотя ранее говорилось, что она слабее всех. Объяснение этому можно найти в табл. 1.2, из которой видно, что частицы-переносчики слабого взаимодействия являются достаточно массивными, тогда как частицы, передающие сильное и электромагнитное взаимодействие, являются безмассовыми. В действительности интенсивность слабого взаимодействия (определяемая соответствующей константой — идея, с которой мы столкнемся в главе 12) является такой, как показано на рис. 7.1, но массивная частица, передающая это взаимодействие, довольно пассивно выполняет свои функции, что приводит
к уменьшению интенсивности этого вида взаимодействия. В главе 14 мы увидим, как вписывается в картину рис. 7.1 гравитационное взаимодействие.
7. Эдвард Виттен, из цикла лекций в память Хайнца Пагельса. г. Аспен, Колорадо, 1997 год.
8. Углубленное обсуждение этой и ряда других смежных идей приведено в книге Steven Weinberg, Dreams of a Final Theory. (Рус. пер.: Вайнберг С. Мечты об окончательной теории. М.: УРСС. 2004.)
Глава 8
1. Эго простая идея, однако, поскольку несовершенство нашего обычного языка приводит иногда к недопониманию, приведем два пояснения. Во-первых, мы считаем, что муравей живет на поверхности Садового шланга. Если бы муравей мог зарываться вглубь шланга, т. е. если бы он мог проникать внутрь резины, из которой сделан шланг, нам бы потребовалось три числа, чтобы указать его местоположение, поскольку нужно было бы указать, как глубоко он закопался. Однако если муравей живет только на поверхности шланга, то чтобы указать его положение, достаточно двух чисел. Отсюда следует необходимость второго пояснения. Даже тогда, когда муравей живет на поверхности шланга, мы можем, если захотим, указывать его положение с помощью трех чисел: обычных положений в направлениях влево-вправо, вперед-назад и вверх-вниз в нашем привычном трехмерном пространстве. Однако когда известно, что муравей живет на поверхности шланга, два числа, упомянутые в тексте, представляют собой минимальный набор величин, однозначно определяющих положение муравья. Именно это имелось в виду, когда мы говорили, что поверхность шланга двумерна.
2. Как ни удивительно, физики Савас Димопулос, Нима Аркани-Хамед и Гия Двали, основываясь на более ранних догадках Игнатиоса Антониадиса и Джозефа Ликкена, смогли показать, что даже если бы свернутые дополнительные измерения были столь велики, что достигали размера в один миллиметр, они могли бы оставаться необнаруженными экспериментально. Причина состоит в том, что ускорители частиц исследуют микромир с помощью сильного, слабого и электромагнитного взаимодействий. Гравитационное взаимодействие, которое при технологически достижимых энергиях остается чрезвычайно слабым, обычно игнорируется. Однако Димопулос с коллегами показали, что свернутые измерения оказывают влияние преимущественно на гравитационное взаимодействие (что выглядит вполне правдоподобно в теории струн); этот эффект вполне мог быть пропущен во всех экспериментах, выполненных до настоящего времени. В ближайшем будущем с использованием высокоточной аппаратуры будут проведены новые эксперименты по изучению гравитационных эффектов, предназначенные для поиска таких «крупных» свернутых измерений. Положительный результат будет означать одно из величайших открытий в истории человечества.
Примечания 257
3. Edwin Abbott, Flatland, Princeton: Princeton University Press, 1991. (Рус. пер.: Эббот Э. Флатляндия. М.: Амфора, 2001.)
4. Письмо А. Эйнштейна к Т. Калуце. Цитируется по книге: Abraham Pais, Subtle Is the Lord. New York: Oxford University Press, 1982, p. 330. (Рус. пер.: Пайс А. Научная деятельность и жизнь Альберта Эйнштейна. М.: Наука, Физматлит, 1989.)
5. Письмо А.Эйнштейна к Т. Калуце. Цитируется по статье: D. Freedman and P. van Nieuwenhuizen, The Hidden Dimensions of Spacetime, Scientific American, 252(1985), 62.
6. Там же.
7. Физики установили, что в многомерную формулировку труднее всего включить такое понятие стандартной модели как киральность. Поэтому, чтобы не перегружать обсуждение, мы не стали рассматривать это понятие в основном тексте. Для читателей, интересующихся этим вопросом, дадим здесь его краткое описание. Представьте, что кто-то показывает вам фильм, демонстрирующий некоторый научный эксперимент, и предлагает необычное задание — определить, показывает ли фильм сам эксперимент или его отражение в зеркале. Поскольку оператор был очень опытным, никаких признаков наличия зеркала на ленте не видно. Можете ли вы решить эту задачу? В середине 1950-х гг. теоретические работы Т. Д. Ли и Ч. Н.Янга, а также экспериментальные результаты Ц. С. By и ее коллег показали, что вы можете решить эту задачу, если на пленке снят подходящий эксперимент. А именно, их работы доказали, что законы мироздания не обладают полной зеркальной симметрией в том смысле, что зеркальные аналоги некоторых процессов, определяемых слабым взаимодействием, не могут существовать в нашем мире, даже если исходные процессы существуют. Таким образом, если, просматривая фильм, вы увидите, что он демонстрирует один из таких запрещенных процессов, вы будете знать, что наблюдаете зеркальное отражение, а не сам эксперимент. Поскольку зеркальное отражение меняет местами левое и правое, работы Ли, Янга и By показали, что Вселенная не обладает полной симметрией левого и правого, или, используя специальную терминологию, что Вселенная является киральной. Именно это свойство стандартной модели (в частности, слабого взаимодействия) физики считали почти невозможным включить в теорию супергравитации высших размерностей. Чтобы избежать недоразумений, отметим, что в главе 10 мы будем обсуждать концепцию теории струн, известную под названием «зеркальной симметрии», но там слово «зеркальная» будет использоваться в совершенно ином смысле.
8. Для читателя, имеющего математическую подготовку, отметим, что многообразие Калаби—Яу представляет собой комплексное кэлерово многообразие с нулевым первым классом Черна. В 1957 г. Калаби высказал предположение, что каждое такое многообразие допускает Риччи-плоскую метрику, а в 1977 г. Яу доказал справедливость этого предположения.
9. Эта иллюстрация была любезно предоставлена Эндрю Хэнсоном из университета штата Индиана, она была создана с использованием графического пакета Mathematica 3-D.
10. Для читателя, имеющего математическую подготовку, заметим, что это конкретное пространство Калаби—Яу представляет собой действительное трехмерное сечение гиперповерхности пятого порядка в комплексном проективном четырехмерном пространстве.
Глава 9
1. Edward Witten, Reflections on the Fate of Spacetime, Physics Today, April 1996, p. 24.
2. Интервью с Эдвардом Виттеном, 11 мая 1998 г.
3. Sheldon Glashow and Paul Ginsparg, Desperately Seeking Superstrings? Physics Today, May 1986, p. 7.
4. Sheldon Glashow. Опубликовано в The Supervorld I, ed. A. Zichichi, New York: Plenum, 1990, p. 250.
5. Sheldon Glashow, Interactions, New York: Warner Books, 1988, p. 335.
6. Richard Feynman. Опубликовано в Superstrings: A Theory of Everything? ed. Paul Davies and Julian Brown, Cambridge, Eng: Cambridge University Press, 1988.
7. Howard Georgi. Опубликовано в The New Physics, ed. Paul Davies, Cambridge: Cambridge University Press 1989, p. 446.
8. Интервью с Эдвардом Виттеном, 4 мая 1998 г.
9. Интервью с Кумруном Вафой, 12 января 1998 г.
10. Цитируется по книге: Robert P. Crease and Charles С. Mann, The Second Creation. New Brunswick, N. J.: Rutgers University Press, 1996, p. 414.
11. Интервью с Шелдоном Глэшоу, 28 декабря 1997 г.
12. Там же.
13. Интервью с Говардом Джорджи, 28 декабря 1997 г. Во время интервью Джорджи также отметил, что экспериментальное опровержение предсказанного распада протонов, которое следовало из предложенной им и Глэшоу первой теории великого объединения (см. главу 7), сыграло существенную роль в его нежелании принять теорию суперструн. Он горько заметил, что его теория великого объединения требует намного больших энергий, чем любая другая теория, когда-либо выносившаяся на суд, и когда его предсказание оказалось неверным, когда «он был нокаутирован природой», его отношение к изучению физики чрезвычайно высоких энергий резко изменилось. Когда я спросил его, не будет ли для него экспериментальное подтверждение теории великого объединения стимулом включиться в наступление на область планковских масштабов, он ответил: «Да, очень может быть»,
14. David Gross, Superstrings and Unification. Опубликовано в Proceedings of the XXIV International Conference on High Energy Physics, ed. R. Kotthaus and J. Kuhn. Berlin: Springer-Verlag, 1988, p. 329.
258 Примечания
15. Сказав это, следует помнить о возможности, указанной в примечании 8 к главе 6, что струны могут иметь значительно больший размер, чем считалось первоначально, и, следовательно, могут стать объектом прямого экспериментального изучения на ускорителях в течение ближайших десятилетий.
16. Для читателя, имеющего математическую подготовку, заметим, что согласно более точной математической формулировке число семейств равно половине абсолютного значения числа Эйлера для пространства Калаби—Яу. Число Эйлера представляет собой сумму размерностей групп гомологий многообразия, где группы гомологии это то, что мы на нашем нестрогом языке назвали многомерными отверстиями. Таким образом, количество семейств, равное трем, следует из того, что число Эйлера для этих пространств Калаби—Яу равно ±6.
17. Интервью с Джоном Шварцем, 23 декабря 1997 г.
18. Для читателя, имеющего математическую подготовку, заметим, что мы ставим в соответствие многообразию Калаби—Яу конечную нетривиальную фундаментальную группу, порядок которой в некоторых случаях определяет знаменатель дробного заряда.
19. Интервью с Эдвардом Виттеном, 4 марта 1998 г.
20. Для читателей, хорошо знакомых с рассматриваемыми вопросами, заметим, что некоторые из этих процессов нарушают закон сохранения лептонного числа, а также СРТ-симметрию (инвариантность относительно изменения знака заряда, четности и направления времени).
Глава 10
1. Отметим для полноты, что хотя большая часть приведенных выше аргументов в равной степени справедлива как для открытых струн (струн со свободными концами), так и для замкнутых струн (которым мы уделяли основное внимание), в рассматриваемом вопросе два типа струн могут, кажется, проявлять различные свойства. Действительно, открытая струна не может быть «насажена» на циклическое измерение. Тем не менее, в результате исследований, сыгравших в конце концов ключевую роль во второй революции суперструн, Джо Польчински из Калифорнийского университета в городе Санта-Барбара и двое его студентов, Джиан-Хюи Дай и Роберт Лей, в 1989 г. продемонстрировали, что открытые струны прекрасно вписываются в схему, которая будет описана в данной главе.
2. Чтобы ответить на вопрос о том, почему возможные энергии однородных колебаний равны целым кратным 1/R, достаточно лишь вспомнить обсуждение квантовой механики (в частности, примера с ангаром) в главе 4. Там мы узнали о том, что согласно квантовой механике энергия, как и деньги, существуют в виде дискретных порций, т. е. в виде целых кратных различных энергетических единиц. В случае однородного колебательного
движения струны во вселенной Садового шланга эта энергетическая единица в точности равна 1/R, как объясняется в основном тексте на основе соотношения неопределенностей. Таким образом, энергия однородных колебаний равна произведению целых чисел на 1 /R.
3. Математически равенство энергий струн во вселенной с радиусом циклического измерения R или 1 /R есть следствие формулы для энергии v/R+wR, где v — колебательное число, а w - топологическое число. Данное уравнение инвариантно относительно одновременных взаимных замен v на w и R на 1/R, т. е. при перестановке колебательных и топологических чисел с одновременной инверсией радиуса. Мы используем планковские единицы, но можно работать и в более привычных единицах, если переписать формулу для энергии через так называемую струнную шкалу 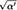 , значение которого примерно равно планковской длине, т.е. 10~33 сантиметра. В результате энергия записывается в виде выражения v/R + wR/', инвариантного относительно взаимной замены v на w и R на '/R, где последние две величины выражены в стандартных единицах расстояния.
, значение которого примерно равно планковской длине, т.е. 10~33 сантиметра. В результате энергия записывается в виде выражения v/R + wR/', инвариантного относительно взаимной замены v на w и R на '/R, где последние две величины выражены в стандартных единицах расстояния.
4. У читателя может возникнуть вопрос, каким образом с помощью струны, намотанной вокруг циклического измерения радиусом Я, можно измерить значение радиуса 1/R. Хотя этот вопрос совершенно правомерен, ответ на него, в действительности, заключается в том, что сам вопрос сформулирован некорректно. Когда мы говорим, что струна намотана на окружность радиуса R, мы с необходимостью используем определение расстояния (чтобы фраза «радиус R» имела смысл). Однако это определение расстояния относится к модам ненамотанной струны, т. е. к колебательным модам. С точки зрения этого определения расстояния (и только этого!) конфигурация намотанной струны выглядит так, что струна обернута вокруг циклической компоненты пространства. Однако с точки зрения другого определения расстояния, соответствующего конфигурациям намотанных струн, топологические моды точно так же локализованы в пространстве, как и колебательные моды с точки зрения первого определения, и радиус, который они «видят», равен 1/ R, что и отмечено в тексте.
Эти пояснения дают некоторое представление о том, почему расстояния, измеренные с помощью намотанных и ненамотанных струн, обратно пропорциональны друг другу. Однако, так как данный момент достаточно тонкий, возможно, имеет смысл привести технические подробности для читателя, склонного к математическому образу мышления. В обычной квантовой механике точечных частиц расстояние и импульс (по существу, энергия) связаны преобразованием Фурье. Иными словами, собственный вектор оператора координаты \х) на окружности радиусом R можно определить как  , где р = v/R, а \р) есть собственный вектор оператора импульса (прямой аналог того, что мы называли общей колебательной модой струны — движение без изменения формы). В теории струн, однако, есть еще один собственный
, где р = v/R, а \р) есть собственный вектор оператора импульса (прямой аналог того, что мы называли общей колебательной модой струны — движение без изменения формы). В теории струн, однако, есть еще один собственный
Примечания 259
вектор оператора координаты  , определяемый состояниями намотанной струны:
, определяемый состояниями намотанной струны:  ,
,
где  — собственный вектор для намотанной струны с
— собственный вектор для намотанной струны с  . Из этих определений немед-
. Из этих определений немед-
ленно следует, что х периодична с периодом 2R, а х периодична с периодом 2 /R, так что х есть координата на окружности радиусом R, а  — координата на окружности радиусом 1 /R. Более конкретно, можно рассмотреть два волновых пакета
— координата на окружности радиусом 1 /R. Более конкретно, можно рассмотреть два волновых пакета  , распространяющихся из начала координат и эволюционирующих во времени, с помощью которых можно дать практическое определение расстояния. Радиус окружности, измеренный с помощью каждого из пакетов, будет пропорционален времени возвращения пакета в исходную точку. Так как состояние с энергией Е эволюционирует с фазовым множителем, пропорциональным Et, видно, что время, а, следовательно и радиус, равны t ~ 1 /Е ~ R для колебательных мод и t ~ 1 /Е ~ 1/R для топологических мод.
, распространяющихся из начала координат и эволюционирующих во времени, с помощью которых можно дать практическое определение расстояния. Радиус окружности, измеренный с помощью каждого из пакетов, будет пропорционален времени возвращения пакета в исходную точку. Так как состояние с энергией Е эволюционирует с фазовым множителем, пропорциональным Et, видно, что время, а, следовательно и радиус, равны t ~ 1 /Е ~ R для колебательных мод и t ~ 1 /Е ~ 1/R для топологических мод.
5. Для читателя, сведущего в математике, отметим, что число семейств колебательных мод струны равно половине абсолютного значения эйлеровой характеристики многообразия Калаби—Яу, как указано в примечании 16 к главе 9. Эта величина равна абсолютному значению разности 
где  обозначает число Ходжа (p,q). С точ-
обозначает число Ходжа (p,q). С точ-
ностью до константы эти значения равны числу нетривиальных гомологии 3-циклов (трехмерных отверстий) и числу гомологии 2-циклов (двумерных отверстий). Таким образом, хотя в основном содержании говорится о полном числе отверстий, более точный анализ показывает, что число семейств зависит от абсолютного значения разности между числами четномерных и нечетномерных отверстий. Выводы, однако, те же самые. Например, если два пространства Калаби—Яу отличаются перестановкой соответствующих чисел Ходжа  и
и  , то число семейств частиц — полное число отверстий — не изменится.
, то число семейств частиц — полное число отверстий — не изменится.
6. Название объясняется тем, что «ромбы Ходжа», математические выражения чисел отверстий различных размерностей для пространств Калаби—Яу, являются зеркальными отражениями друг друга для каждой зеркальной пары.
7. Термин зеркальная симметрия используется в физике и в других контекстах, совершенно не связанных с данным, например, в связи с понятием киральности, т. е. в связи с вопросом о том, является ли Вселенная инвариантной относительно замены правого на левое (см. примечание 7 к главе 8).
Глава 11
1. Для читателя, склонного к математической строгости рассуждений, будет понятно, что вопрос состоит в том, является ли топология пространства динамической, т. е. может ли она меняться во времени. Отметим, что хотя представление о динамических изменениях топологии часто используется в этой книге, на практике обычно рассматривается
однопараметрическое семейство пространственно-временных многообразий, чья топология меняется при изменении параметра семейства. Формально этот параметр не является временем, но в определенном контексте может с ним отождествляться.
2. Для математически подкованного читателя отметим, что процедура включает сдутие рациональных кривых на многообразии Калаби—Яу. Далее используется тот факт, что при определенных условиях образовавшаяся сингулярность может быть устранена серией последовательных раздутий.
3. К. С. Cole, New York Times Magazine, October 18, 1987, p. 20.
Глава 12
1. Цитируется по книге: John D. Barrow, Theories of Everything. New York: Fawcett-Columbine, 1992, p. 13. (В рус. пер. цитата есть в книге: Кузнецов Б. Г. Эйнштейн: Жизнь. Смерть. Бессмертие. М: Наука, 1980, с. 363.)
2. Кратко поясним различия между пятью теориями струн. Для этого отметим, что колебательные возбуждения вдоль струнной петли могут распространяться по часовой стрелке и против нее. Теории струн типов IIА и IIB отличаются тем, что в последней теории колебания в обоих направлениях идентичны, а в первой теории противоположны по форме. Противоположность в данном контексте имеет точный математический смысл, но нагляднее всего ее можно представлять в терминах вращений колебательных мод в каждой теории. В теории типа IIВ оказывается, что все частицы вращаются в одном направлении (у них одна и та же киральность), а в теории типа IIА — в разных направлениях (у них разная киральность). Тем не менее, в каждой теории реализуется суперсимметрия. Две гетеротические теории имеют аналогичные, но более эффектные отличия. Все моды колебаний по часовой стрелке выглядят так же, как и моды струн типа II (если рассматривать только колебания по часовой стрелке, то теории струн типов ПА и IIB идентичны), но колебания против часовой стрелки совпадают с колебаниями исходной теории бозонных струн. Хотя в бозонных струнах возникают неразрешимые проблемы, если рассматривать их колебания в обоих направлениях, в 1985 г. Дэвид Росс, Джеффри Харви, Эмиль Мартинек и Райан Ром (все они в то время работали в Принстонском университете и их прозвали «Принстонский струнный квартет») показали, что при использовании этих струн в комбинации со струнами типа II получается вполне согласованная теория. Однако в этом союзе была странная особенность, известная со времен работ Клода Лавлейса из университета Ратчерса 1971 г. и Ричарда Броуэра из Бостонского университета, Питера Годдарда из Кембриджского университета и Чарльза Торна из Гейнсвилльского университета (штат Флорида) 1972 г. А именно, для
260 Примечания
бозонной струны требовалось 26 пространственно-временных измерений, а для суперструны, как обсуждалось, требовалось 10. Так что гетеротические струны (от греческого  , т. е. разный)
, т. е. разный)
Не нашли, что искали? Воспользуйтесь поиском: