Построение и обозначение уклонов и конусности

Уклон – величина, характеризующая наклон одной прямой линии к другой прямой. Уклон i отрезка ВС относительно отрезка ВА определяют отношением катетов прямоугольного треугольника АВС, т.е.: i = АС/АВ = tg a. Уклон выражают дробью или в процентах. По ГОСТ 2.307-68 перед числом, определяющим уклон, наносят условный знак в виде острого угла, направленного в сторону уклона

Конусность с – отношение диаметра основания конуса D к его высоте L. Для усеченного конуса конусность определяют по формуле с = (D – d)/ L, где d – диаметр усеченного конуса. По ГОСТ 2.307-68 перед числом, характеризующим конусность, находится условный знак конусности в виде равнобедренного треугольника с вершиной, направленной в сторону вершины конуса

Сопряжение линий

Сопряжением называют плавный переход прямой в дугу окружности (рисунок 9) или одной дуги в другую. Для построения сопряжений надо знать величину радиуса сопряжений, найти центры, из которых проводят дуги, т.е. центры сопряжений. Затем нужно найти точки, в которых одна линия переходит в другую, т.е. точки сопряжений.

При построении чертежа сопрягающиеся линии нужно доводить точно до этих точек. Точка сопряжения дуги окружности и прямой лежит на перпендикуляре, опущенном из центра дуги на сопрягаемую прямую, или на линии, соединяющей центры сопрягаемых дуг. Следовательно, для построения любого сопряжения дугой заданного радиуса нужно найти центр сопряжения и точку (точки) сопряжения.

Сопряжение дуги и прямой дугой заданного радиуса

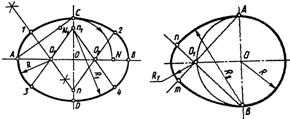
Сопряжение двух пересекающихся прямых дугой заданного радиуса	Построение овала и овоида
Построение эллипса
Сопряжение двух дуг дугой заданного радиуса   Для внешнего касания «+» Для внутреннего касания «-»   Для смешанного касания «+» и «-»

Не нашли, что искали? Воспользуйтесь поиском: