ОПРЕДЕЛЕНИЕ РАДИУСОВ КРИВИЗНЫ. Цель работы: изучить конструкцию сферометра и методику определения с его помощью радиусов кривизны выпуклых и вогнутых поверхностей

СФЕРИЧЕСКИХ ПОВЕРХНОСТЕЙ

Цель работы: изучить конструкцию сферометра и методику определения с его помощью радиусов кривизны выпуклых и вогнутых поверхностей, измерить радиус кривизны исследуемой поверхности.

Приборы и принадлежности: сферометр ИЗС-8, измеряемая сферическая поверхность, эталонная плоскость.

Теория работы

Во многих отраслях промышленности используются сферические поверхности, радиусы кривизны которых необходимо измерять и контролировать с высокой точностью. Одним из основных методов измерения параметров сферических поверхностей является оптический. Оптические контрольно-измерительные приборы позволяют измерять объекты с радиусами кривизны от долей миллиметра до нескольких тысяч метров. Например, при применении автоколлимационного метода для измерений радиусов кривизны сферических поверхностей от 0,5 мм до 100 мм используются автоколлимационные микроскопы, от 50 до 500 мм – длиннофокусные микроскопы, от 500 до 5000 мм - длиномерные измерительные машины, от 1500 до 2000 мм – зрительные трубы с длиннофокусными объективами. Для измерений в диапазоне от 8 до 330 мм используется интерферометрический метод, от 5000 мм – метод колец Ньютона. Точность оптических методов доходит до 0,001 %.

Особенно актуальны высокоточные измерения параметров поверхностей в оптической промышленности, где измерение радиусов кривизны сферических поверхностей и проверка их формы – важная и обязательная контрольная операция при изготовлении оптических деталей. Отклонение поверхностей от заданной кривизны приводит к нарушению конструктивных характеристик оптических систем и к ухудшению качества изображения. Не менее важен контроль сферических поверхностей и в точном машиностроении.

Для измерения радиусов кривизны выпуклых и вогнутых сферических поверхностей изделий больших размеров и большого веса в диапазоне от 80 до 40000 мм применяется сферометр ИЗС-8 c набором измерительных колец разного диаметра (рис. 1). Внутри литого металлического корпуса 1 находится измерительный стержень со стеклянной миллиметровой шкалой длиной 30 см – пиноль. Пиноль подвешена на капроновой нити и перемещается вдоль своей оси в подшипниках качения. Подъем пиноли осуществляется путем накручивания нити на валик при вращении маховичка 2, опускание до соприкосновения с измеряемой поверхностью – путем раскручивания нити.

Отсчет по миллиметровой шкале производится с помощью микроскопа 3 со спиральным окулярным микрометром 4 с ценой деления 0,001 мм. Увеличение микроскопа 62^х. Измерительная шкала освещается с помощью зеркала 5. Сферометр снабжен набором сменных измерительных колец 6. Каждое кольцо имеет три опорных стальных шарика 7, которыми сферометр устанавливают на измеряемую поверхность. Шарики расположены относительно друг друга под углом 120⁰.

Рис. 1 Рис. 2

Измерительное кольцо надевается на посадочную поверхность и закрепляется гайкой 8. Выбор нужного измерительного кольца осуществляется по принципу наименьшего отличия диаметров кольца и измеряемого изделия.

Для определения радиуса кривизны поверхности сферометр с измерительным кольцом осторожно ставят на измеряемую поверхность, опускают пиноль до соприкосновения с ней и измеряют стрелку прогиба h.

Найдем связь стрелки прогиба с радиусом кривизны измеряемой выпуклой поверхности (рис. 2). Стрелка прогиба h = АD. Радиус измерительного кольца r =

= ВО – радиус окружности, проходящей через центры всех трех шариков кольца. Радиус кривизны измеряемой поверхности R - отрезок СD. Из рисунка видно, что CG = R + r, где r - радиус шарика кольца.

По известной из геометрии теореме (перпендикуляр ОВ, опущенный из любой точки окружности на диаметр 2СG, есть среднее пропорциональное между отрезками диаметра ВG и 2СG – bG), имеем:

(1)

Отрезки АD и ВС равны, т. к. точка А расположена ниже точки В на величину r, а точка D расположена ниже точки G также на величину r, поэтому ВG = h. Тогда формула (1) примет вид: откуда

(2)

Для вогнутой поверхности (3)

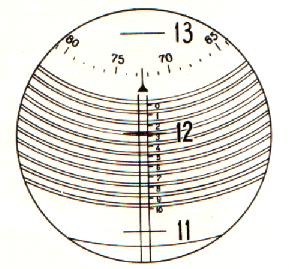
Рис. 3

Не нашли, что искали? Воспользуйтесь поиском: