Свойства взаимности

Саратовский государственный технический университет

Имени Гагарина Ю.А

Исследование линейной электрической цепи постоянного тока

Методические указания

к выполнению лабораторной работы

по курсу «Теоретические основы электротехники»

для студентов специальностей

200300, 200500 (направление 654100), 210300 (направление 652000),

210100 (направление 651900), 100400 (направление 650900), 180500 (направление 654500),

120200 (направление 651400), 120100 (направление 657800), 200700 (направление 654200)

Одобрено

редакционно-издательским отделом

Саратовского государственного технического университета

имени Гагарина Ю.А.

Саратов 2014

Цель работы: экспериментально исследовать основные законы, принципы, теоремы, эквивалентные преобразования, которым подчиняются линейные электрические цепи постоянного тока.

Основные понятия

Законы Кирхгофа

Электрическая цепь называется линейной, если она состоит из линейных элементов. Линейным элементом называется такой элемент электрической цепи, вольт-амперная характеристика (ВАХ) которого линейна, то есть сопротивление его постоянно и не зависит от величины протекающего по нему тока. Все электрические цепи подчиняются первому и второму законам Кирхгофа [1], [2], [3], [4]. Расчет цепей на основании непосредственного применения законов Кирхгофа сводится к определению токов схемы по известным ЭДС и сопротивлениям. На заданной схеме выбирают произвольное направление всех токов ветвей (желательно выбрать направление тока по направлению ЭДС, действующей в этой ветви, если ЭДС в ветви есть). Нумеруют все узлы схемы. Узлом называется точка, в которой соединяются три и более ветвей (проводников). Ветвь - это участок цепи с последовательным соединением элементов, через которые протекает один и тот же ток. Количество уравнений по первому закону Кирхгофа (узловых уравнений) будет на единицу меньше числа узлов:

N₁=У-1,

где У- количество узлов в исходной схеме.

Чтобы определить количество уравнений по второму закону Кирхгофа нужно вычесть из числа неизвестных (совпадает с числом ветвей схемы, без ветвей с источниками тока, так как в последних ток будет равен току источника), число уравнений, составленных по первому закону Кирхгофа:

N₂=В-(У-1),

где В- количество ветвей без источников тока в исходной схеме. Столько же неизвестных токов, которые нужно определить.

Первый закон Кирхгофа гласит: Алгебраическая сумма токов в любом узле равна нулю, то есть, сколько тока вошло в узел - столько и выйдет. Если ток входит в узел, то он берется со знаком "+", а если выходит, то со знаком "-". (Можно использовать обратное правило знаков: если ток входит в узел, то он берется со знаком "-", а если выходит, то со знаком "+"). Правило знаков определяется перед началом решения задачи и в процессе решения не меняется. Математически первый закон Кирхгофа записывается так:

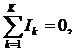
где k — номер ветви, K — число ветвей, соединенных в узле.

Второй закон Кирхгофа гласит: В любом замкнутом контуре алгебраическая сумма напряжений на ветвях (или элементах, входящих в контур), равна нулю:

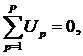
где p — номер ветви (или элемента), P — число ветвей (или элементов), входящих в контур.

В потенциальном поле напряжение между двумя любыми точками равно разности потенциалов между ними: 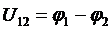, причем U₁₂ > 0 если φ₁ > φ₂.

Если напряжение источников выразить через ЭДС и перенести в правую часть уравнения второго закона Кирхгофа, то оно примет вид:

или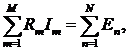

где m — номер сопротивления, входящего в данный контр, M — общее число сопротивлений, входящих в контур, n — номер ЭДС, входящей в данный контр, N — общее число ЭДС, входящих в контур.

Отсюда вытекает вторая формулировка второго закона Кирхгофа: Алгебраическая сумма падений напряжений на сопротивлениях, входящих в любой замкнутый контур равна алгебраической сумме ЭДС, действующих в этом контуре. Если напряжение или ЭДС совпадают с направлением обхода контура (выбирается произвольно), то берется знак "+", в противном случае - знак "-". Математически второй закон Кирхгофа записывается так:

Для каждого контура можно составить уравнение по второму закону Кирхгофа, однако для решения задачи требуются не все контура, а только независимые, которыми называют такие контура, в которые входит хотя бы одна ветвь, не вошедшая ни в один другой контур. Эта ветвь называется внешней ветвью контура и ток в этой ветви равен контурному току (см. метод контурных токов).

Второй закон Кирхгофа справедлив для любого замкнутого пути, проходящего через любые точки схемы (мысленного контура), даже если между этими точками разрыв цепи, который считается бесконечным сопротивлением. Например, для контура «54135» схемы рис. 1 уравнение II закона Кирхгофа может быть записано:

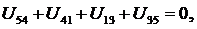
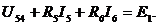
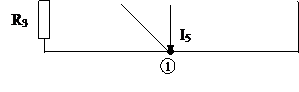
Рис. 1

Число уравнений, составленных по I и II законам Кирхгофа, равно числу неизвестных токов в ветвях схемы N = N₁+N₂ и совпадает с количеством ветвей, не содержащих источники тока. Решив систему уравнений, определяют токи в ветвях схемы.

Принцип наложения

В любой линейной электрической цепи с несколькими источниками энергии, ток (напряжение) любой ветви равен алгебраической сумме частичных токов (напряжений) этой ветви вызванных действием каждого из источников в отдельности [1], [2].

где I_k -ток ветви «k»; I_k(En) I_{k(Jm) —} частичные токи ветви «k» вызванные действием источника ЭДС E_n и источника тока J_m соответственно; g_kn — взаимная проводимость ветвей «k» и «n»; h_km – коэффициент передачи тока источника тока J_m в ветвь «k»; U_k — напряжение на сопротивлении R_k, включенного в ветвь «k» и через которое протекает ток I_k; U_k(En), U_k(Jm) - частичные напряжения на сопротивлении R_k, вызванные действием источника ЭДС E_n и источником тока J_m соответственно; N – полное количество источников ЭДС, действующих в цепи; M - полное количество источников тока, действующих в цепи.

Примечание: надо понимать, что источник ЭДС Е₁ включен в первую ветвь, источник ЭДС Е₂ включен во вторую ветвь и т.д., однако источник тока J₁ в первую ветвь не входит, источник тока J₂ во вторую ветвь не входит, источники тока находятся в своих собственных ветвях, токи которых совпадают с величиной соответствующего источника тока.

Правило знаков: частичный ток или напряжение входит в выражение полного тока I_k или напряжения U_k с положительным (отрицательным) знаком, если его направление совпадает (противоположно) с выбранным направлением тока I_k или напряжения U_k.

При расчете частичного тока от действия какой-либо ЭДС, например, E_n, или тока источника тока J_m, все остальные источники энергии удаляются из схемы, но остаются включенными их внутренние сопротивления. Если источник ЭДС идеальный, его внутреннее сопротивление R_вн = 0. Если источник тока идеальный, то R_вн = ∞.

Принцип наложения вытекает из общего физического принципа независимости действия сил в линейных системах (принципа суперпозиции), согласно которому реакция от совокупного действия нескольких сил равна сумме реакций от действия каждой из сил в отдельности.

Принцип наложения несправедлив для мощностей, т.к. мощность — квадратичная функция тока или напряжения.

Свойства взаимности

Для любой линейной электрической цепи справедливо свойство взаимности:

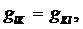
где g_lk — взаимная проводимость «l» и «k» ветвей, R_lk — взаимное сопротивление «l» и «k» узлов.

Если в схеме (рис. 2,а) действует, например, единственный источник ЭДС E_k, в ветви «k», и вызывает ток в ветви «l» I_l, то, будучи перенесенным в ветвь «l» и действуя в направлении тока I_l (рис. 2,б), он вызовет в ветви «k» ток I_k, направленный в ту же сторону, что и E_k, и равный току I_l в схеме (рис. 2,а) [2], [3].

Рис. 2

Ток любой ветви схемы можно найти, пользуясь принципом наложения через ЭДС и взаимную проводимость. В схеме (рис. 2,а) I_l=g_lkE_k, в схеме (рис. 2,б) I_k=g_klE_l. Так как E_k=E_l и g_lk=g_kl, то I_k=I_l. Это равенство называют свойством взаимности (обратимости) для источника ЭДС и тока в пассивной ветви.

Пользуясь методом узловых потенциалов и принципом наложения для напряжений можно обосновать свойство взаимности для источника тока и напряжения пассивной ветви.

(а) (б)

Рис. 3

Если в схеме (рис. 3,а) действует единственный источник энергии (источник тока J_l), подключенный к узлам «l» и «0», и вызывает между узлами «k» и «0» напряжение U_k0 , то тот же источник тока, будучи подключенным к узлам «k» и «0», вызовет между узлами «l» и «0» в схеме (рис. 3,б) напряжение U_l0 , равное напряжению U_k0 в схеме (рис. 3,а), то есть J_l=J_k , U_l0=U_k0 [3], [4].

Не нашли, что искали? Воспользуйтесь поиском: