
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Обзор методов цифровой обработки изображений 1 страница
Все основное множество методов, которые решают данные задачи, делится на методы обработки в частотной и пространственной областях. Для обработки изображений в пространственной области наибольшее распространение получили методы:
· Ранговые алгоритмы
· Разностные методы
· Гистограммные методы
· Метод локальных контрастов
· Координатный метод анализа изображения
· Спектральный метод анализа изображения.
К преимуществам методов обработки изображений в пространственной области относится возможность быстрой обработки в масштабе реального времени, а к недостаткам - ограниченность функциональных возможностей и недостаточная эффективность. При рассмотрении методов обработки изображений всегда остро стоит вопрос выбора критериев оценки качества их преобразования. Хотя способы обработки изображений в частотной области и достаточно развиты, но требуют значительных вычислительных затрат и для решения практических задач применяются реже.
1.6 Ранговые алгоритмы
Существующие методы цифровой обработки изображений с позиций использования вычислительных средств можно разделить на две категории - структурированные и неструктурированные методы.
Структурированные методы – такие, которые построены на использовании крупных вычислительных (программных) блоков, оперирующих векторами отсчетов, а не отдельными отсчетами изображений. Cреда MATLAB позволяет реализовывать методы обработки изображений, оперирующие не только с векторами, но и с массивами отсчетов.
Неструктурированные методыте, которые нельзя представить более крупными стандартными блоками, чем обычные для существующих цифровых вычислительных машин арифметико-логические операции над отдельными отсчетами сигналов. Неструктурированные методы, как правило, возникают на начальной стадии поиска решения содержательных задач обработки изображений и по мере нахождения решения перерастают в структурированные.
Рассмотрим класс структурированных нелинейных алгоритмов, которые осуществляют преобразование вида:
| )], |
| ( |
| [ |
| ) |
| ( |
| ] |
| [ |
| k |
| k |
| k |
| x |
| F |
| x |
| F |
| y |
| y |
| = |
| = |
| = |
где  - нелинейная функция, которая определяется некоторым подмножеством рангов и (или) порядковых статистик выборки, образованной отсчетами сигнала из некоторой окрестности данного элемента, в последовательности упорядоченных отсчетов сигнала. Поэтому класс алгоритмов называется ранговыми алгоритмами.
- нелинейная функция, которая определяется некоторым подмножеством рангов и (или) порядковых статистик выборки, образованной отсчетами сигнала из некоторой окрестности данного элемента, в последовательности упорядоченных отсчетов сигнала. Поэтому класс алгоритмов называется ранговыми алгоритмами.
Преимуществом ранговых алгоритмов является их отличие от методов линейной фильтрации, они лишены такого характерного недостатка как пространственная инерционность, которая заключается в том, что при использовании линейных фильтров влияние отдельных деталей изображения проявляется на результирующем изображении на расстоянии порядка размеров апертуры фильтра. Это заметно в частности в размывании границ деталей при сглаживании изображений, в искажении формы деталей при их выделении из фона и т.п.
На первый взгляд может показаться, что вследствие переупорядочивания данных в вариационный ряд ранговые алгоритмы не используют пространственных связей между элементами изображений, и это является принципиальным недостатком. Действительно, ранговые алгоритмы инвариантны к пространственным связям и даже к размерности сигнала. Однако, как ни удивительно, это свойство является не недостатком, а преимуществом ранговых алгоритмов, еще одной стороной их адаптивного характера.
Пространственные связи между элементами изображения, определяемые, например, принадлежностью их к одной детали, проявляют себя в вариационном ряду через параметры условной гистограммы распределения значений сигнала в окрестности данного элемента.
Ранговые алгоритмы могут использоваться во всех процедурах обработки изображений – стандартизации, сглаживания, усиления детальности, выделения объектов из фоновой части, выделения границ, определения статистических характеристик и т.д.
Ранговые алгоритмы локально-адаптивны по своей сути, поскольку их параметры являются функциями локальной характеристики изображений - локальной гистограммы. Термин "ранговые алгоритмы" в обработке изображений появился относительно недавно, когда множество алгоритмов, которые фактически относятся к классу ранговых, были уже достаточно известны. Для фильтрации импульсных помех и сглаживания изображений давно используется предложенный Тьюки алгоритм медианной фильтрации. Известны также алгоритмы экстремальной фильтрации, которые используют значения минимума и максимума в окрестности. Все эти алгоритмы можно рассматривать как частные случаи широкого класса ранговых алгоритмов.
Методы ранговых преобразований позволяют осуществить нелинейное усиление высокочастотной составляющей изображения. Это приводит к повышению детальности изображений, однако сопровождается уменьшением контрастности тонкоструктурных объектов. Возможным вариантом устранения этого недостатка является использование взвешенных ранговых преобразований.
Кроме применений для сглаживания, усиления детальности, выделения деталей изображений и границ деталей, ранговые алгоритмы можно употреблять для решения многих других задач обработки изображений, в частности, для диагностики статистических характеристик искажений видеосигнала, стандартизации изображений, определения статистических характеристик видеосигнала и измерения текстурных признаков.
Одним из наиболее простых примеров ранговой обработки изображений является медианная фильтрация. Преимуществом данного алгоритма является простота его реализации. К недостаткам же относится то, что сглаживание изображений с помощью медианной фильтрации приводит к устранению границ деталей изображения [3].
1.7 Разностные методы
Психофизические эксперименты показывают, что фотографическое или телевизионное изображение с подчеркнутыми границами часто воспринимается субъективно лучше, чем фотометрически совершенная продукция. Процедуру подчеркивания границ реализуют с использованием методов нечеткого маскирования (разностных методов).
Суть этих методов состоит в следующем. Исходное изображение сканируют двумя апертурами с различной разрешающей способностью. В одной апертуре разрешающая способность отвечает норме, а во второй - ниже нормы. В результате образуются два массива: массив элементов изображения  и массив элементов нечеткого изображения
и массив элементов нечеткого изображения  . Результат формируется путем вычитания изображений по алгоритму:
. Результат формируется путем вычитания изображений по алгоритму:
 (1.4)
(1.4)
где  - коэффициент пропорциональности. Оставляющей риантом этого метода является выражение:
- коэффициент пропорциональности. Оставляющей риантом этого метода является выражение:
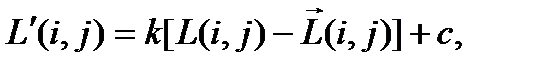 (1.5)
(1.5)
где  - коэффициент усиления контрастности;
- коэффициент усиления контрастности; 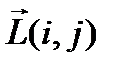 - среднеарифметическое значение яркостей элементов скользящей апертуры с центром в элементе с координатами
- среднеарифметическое значение яркостей элементов скользящей апертуры с центром в элементе с координатами  размером
размером  элементов. В зависимости от размеров апертуры скользящего окна результат действия разностных методов находится в пределах от локального усиления контуров до выравнивания общего фона на изображении. Существуют другие, более сложные модификации метода нечеткого маскирования. К таким методам можно отнести методы коррекции фоновой составляющей, на которую накладывается высокочастотная текстура объектов и деталей изображения. Использование этого подхода приводит к усилению локальных контрастов деталей различных размеров и улучшению визуального восприятия изображений. Известны также методы представления детальной с изображения через локальный контраст. Они позволяют создавать новые классы методов нечеткого маскирования, базирующиеся на нелинейных преобразованиях локальных контрастов. Это в свою очередь говорит об общности различных методов преобразования контрастности изображений.
элементов. В зависимости от размеров апертуры скользящего окна результат действия разностных методов находится в пределах от локального усиления контуров до выравнивания общего фона на изображении. Существуют другие, более сложные модификации метода нечеткого маскирования. К таким методам можно отнести методы коррекции фоновой составляющей, на которую накладывается высокочастотная текстура объектов и деталей изображения. Использование этого подхода приводит к усилению локальных контрастов деталей различных размеров и улучшению визуального восприятия изображений. Известны также методы представления детальной с изображения через локальный контраст. Они позволяют создавать новые классы методов нечеткого маскирования, базирующиеся на нелинейных преобразованиях локальных контрастов. Это в свою очередь говорит об общности различных методов преобразования контрастности изображений.
Изображения, которые формируются во время различных исследований, часто не используют весь диапазон возможных градаций яркостей. Это предопределяет их низкую информативность. Контрастность изображения, яркости элементов которого расположены в узком промежутке возможных значений, низкая. Один из методов повышения качества таких изображений состоит в нелинейном преобразовании значений видеосигнала, в частности, в расширении области используемых значений градаций яркости на максимально возможный диапазон. Часто в основе таких преобразований лежит линейное растяжение или гамма-коррекция. Благодаря простой программной реализации и относительно высокому быстродействию, этот метод получил широкое применение. Преобразование, реализующее растяжение (рисунок 1.5):
 , (1.6)
, (1.6)
где  , - соответственно минимальная и максимальная яркости элементов изображения;
, - соответственно минимальная и максимальная яркости элементов изображения;  - элемент изображения с координатами
- элемент изображения с координатами  ;
;
R - максимальное значение яркости элементов изображения.
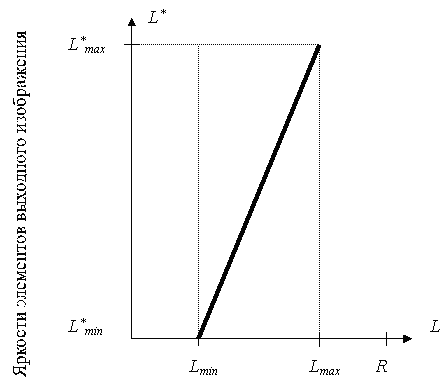
Рисунок 1.5 - Линейное растяжение яркостей элементов изображения
Выражение (1.6) осуществляет одинаковое растяжение для элементов разной яркости.
Методы линейного растяжения и гамма-коррекции являются базовыми при построении табличных методов. Они имеют ряд недостатков, среди которых слабая адаптация к характеристикам конкретного изображения, поскольку в качестве характеристик изображения они используют лишь минимальное  и максимальное
и максимальное  значения яркостей его элементов. Вместе с тем никак не учитываются локальные особенности изображения и структура распределения яркостей элементов. С другой стороны, по закону формирования уровня адаптации зрительный механизм человека приспосабливается к определенному уровню яркости объекта. В этом случае уровень яркости отвечает усредненной яркости
значения яркостей его элементов. Вместе с тем никак не учитываются локальные особенности изображения и структура распределения яркостей элементов. С другой стороны, по закону формирования уровня адаптации зрительный механизм человека приспосабливается к определенному уровню яркости объекта. В этом случае уровень яркости отвечает усредненной яркости  всех элементов изображения:
всех элементов изображения:
 , (1.7)
, (1.7)
где  - размеры изображения
- размеры изображения  .
.
Методы линейного растяжения и гамма-коррекции имеют еще один существенный недостаток, который состоит в том, что если яркости элементов изображения занимают максимально допустимый диапазон, а яркости элементов важных деталей – узкий промежуток, то улучшить контраст таких объектов этими методами достаточно тяжело. Использование других методов, которые решили бы эту задачу, связано с увеличением вычислительной сложности.
Итак, если динамический диапазон яркостей элементов изображения в целом приемлем, но значения градаций информативно важных объектов не распределены равномерно во всем промежутке, тогда методы растяжения не дают эффективного усиления контрастности. В качестве решения этой проблемы предложен метод кусочного растяжения с фиксацией узловой точки. Этот метод является обобщением известных методов растяжения и имеет более широкие функциональные возможности относительно улучшения разных классов изображений. Это касается, в первую очередь, изображений, динамический диапазон яркостей которых в общем приемлемый, а диапазон яркостей информативной части - узкий. В целом предложенный подход к преобразованию изображений позволяет существенно повысить эффективность их обработки простыми алгоритмическими средствами. Он служит основой построения быстрых методов повышения контраста изображений.
Экспериментальные исследования предложенного метода показали его преимущества в сравнении с известными методами того же класса.
1.8 Гистограммные методы
Гистограмма распределения яркостей реального изображения, подвергнутого линейному квантированию, имеет ярко выраженный подъем в сторону малых уровней. Поэтому мелкие детали на темных участках видимы плохо, а сами изображения характеризуются низким контрастом. С целью повышения контраста таких изображений используют методы видоизменения гистограммы. Суть этих методов состоит в преобразовании яркостей исходного изображения таким образом, чтобы гистограмма распределения яркостей приобрела желательную форму.
Оптимальным с точки зрения зрительного восприятия человеком является изображение, элементы которого имеют равномерное распределение яркостей. Множество исследователей получили ряд улучшенных изображений путем выравнивания гистограммы, то есть в каждом случае они стремились достичь равномерности распределения яркостей обработанного изображения. Процедура выравнивания гистограммы состоит из следующих действий:
1. Вычисляется гистограмма распределения яркостей элементов изображения;
2. Строится нормированная кумулятивная гистограмма;
3. Формируется новое изображение.
Это преобразование эффективно для улучшения визуального качества низко контрастных деталей. Существует также ряд известных методов видоизменения гистограммы, которые приводят к получению изображений с заранее заданным распределением. Описанные методы преобразования гистограммы могут быть глобальными, то есть использовать информацию обо всем изображении, и скользящими, когда для преобразования используются локальные области изображения. Рассмотренные выше подходы служат основой широкого класса гистограммных методов преобразования изображений.
1.9 Метод локальных контрастов
Одной из наиболее удобных форм представления информации является изображение. Существуют различные подходы к визуализации. Одним из существенных недостатков этих методов является то, что в большинстве своем они обеспечивают формирование слабоконтрастных изображений. Это вызывает необходимость развития методов их обработки. Поэтому основная цель методов улучшения состоит в преобразовании изображений к более контрастному и информативному виду. Довольно часто на изображении присутствуют искажения в определенных локальных областях, которые вызваны дифракцией света, недостатками оптических систем или расфокусировкой. Это порождает необходимость выполнения локальных преобразований изображения.
Рассмотрим известную технологию повышения качества изображений, которая основывается на преобразовании локальных контрастов. Основная ее идея состоит в том, что для каждого элемента изображения сначала определяется локальный контраст, а потом происходит его нелинейное усиление и восстановление яркости данного элемента изображения из уже скорректированного локального контраста.
Рассмотренный метод является классическим примером методов класса преобразования локальных контрастов. Эти методы позволяют решать задачи не только улучшения визуального качества изображений, но и реализовывать как высокочастотную, так и низкочастотную фильтрацию с помощью применения различных функций преобразования локальных контрастов.
Контрастирование может использоваться как для улучшения изображений. Как правило, при контрастировании преобразуется и яркость. Основное правило для оценки применимости контрастирования: монотонно нарастающие характеристики преобразования яркости в основном используются для повышения качества изображений. Контрастирование может применяться как для ахроматических, так и для цветных изображений.
1.10 Координатный метод анализа изображения
Как первичный преобразователь оптической информации фотоприбор с зарядовой связью (ФПЗС) обладают целым рядом положительных свойств, к которым можно отнести: высокую разрешающую способность, малые габариты и стоимость, высокую надежность, а также, что наиболее важно, эти приборы представляют возможность получать обширную информацию о контролируемом объекте.
Отмеченные свойства совместно с использованием современных средств микропроцессорной техники позволят разрабатывать эффективные системы сбора первичной информации. В подобных оптоэлектронных системах выделение интересующей информации об объекте контроля в основном возлагается на математические и алгоритмические методы обработки получаемых от ФПЗС первичных изображений. Это позволяет создавать гибкие автоматизированные системы, способные быстро адаптироваться к изменяющимся условиям современного производства. Использование матричных ФПЗС (по сравнению с линейными) позволяет создавать более универсальную аппаратуру, а так же избежать необходимости решения задачи синхронизации с движущимся полотном ткани, так как матричные ФПЗС предоставляют для анализа целостностное двумерное изображение контролируемого объекта. В качестве аппаратурной части таких систем могут использоваться серийно выпускаемые ФПЗС преобразователи и микроэлектронные средства цифровой обработки сигналов.
На рисунке 1.6 изображена возможная схема системы для обнаружения и устранения дефектов шва с использованием матричных ФПЗС. Отраженный от поверхности ткани световой поток, несущий информацию о структуре ткани, воспринимается матричными ФПЗС преобразователями 1.
Преобразователи формируют электронное изображение исследуемого участка поверхности ткани, которое преобразуется посредством АЦП 2 в цифровую форму в виде матрицы чисел, пропорциональных освещенности элементов матрицы ФПЗС и образующих цифровое изображение участка поверхности ткани. Полученные цифровые изображения поступают на обработку в ЭВМ 3. В ЭВМ с помощью разработанных алгоритмов из полученных цифровых изображений выделяется информация о расположении уточных нитей, а следовательно, и о дефекте шва. Далее на основании данных о величине и знаке перекоса утка формируется управляющее воздействие на механизм правки утка 4. Посредством блока управления осветителями 6 имеется возможность оперативной коррекции режима работы осветителями 5. Результаты дефекта шва могут быть так же выведены на индикатор 7.

(1 - фотоприемники на ФПЗС; 2 - АЦП; 3 - ЭВМ;
4 - механизм правки утка; 5 - осветители; 6 - блок управления осветителями; 7 - индикатор; 8 – ткань)
Рисунок 1.6 - Cхема правки утка и измерения плотности ткани с использованием матричных ФПЗС
Основной исследовательской задачей, возникающей при разработке систем правки перекоса дефектов шва с использованием матричных фотоприборов с зарядовой связью (ФПЗС), является разработка методик анализа первичных цифровых изображений с целью выделения информации о дефекте шва.
Разрабатываемые алгоритмы должны обеспечивать устойчивое и достоверное измерение величины и знака перекоса уточных нитей, а также и плотности ткани для широкого ассортимента тканой продукции, в том числе и для тканей со сложными типами переплетений. Причем, к разрабатываемым алгоритмам анализа цифровых изображений должны быть предъявлены жесткие требования по быстродействию, что необходимо для обеспечения работы системы в реальном масштабе времени с учетом необходимости обработки большого объема информации. Время, затрачиваемое на анализ первичного цифрового изображения для рассматриваемой системы регулирования, является чистым запаздыванием и поэтому оно должно быть минимальным. Отмеченные требования накладывают существенные ограничения на разрабатываемые алгоритмы обработки изображений. Применяемые для анализа изображения алгоритмы должны обеспечивать высокую скорость анализа. При обработке зашумленных цифровых изображений, а так же при работе на тканях со сложными типами переплетений требуется предварительная обработка изображений для устранения зашумленности и адаптации к рисункам переплетений. Это приводит к дополнительному увеличению времени анализа изображения и, соответственно, времени запаздывания в системе регулирования, изображенной на рисунке 1.6.
Указанные требования говорят о необходимости разработки высокоэффективных алгоритмов анализа изображений, удовлетворяющих таким противоречивым требованиям, как высокая достоверность результатов анализа для широкого ассортимента тканей и высокая скорость обработки реальных сигналов, необходимая для обеспечения возможности работы системы регулирования в реальном масштабе времени.
Координатный метод обеспечивает большую, по сравнению со спектральным методом, скорость обработки информации. Спектральный метод обладает преимуществами при обработке зашумленных изображений, а так же при работе на тканях со сложными типами переплетений.
Матричный ФПЗС преобразователь представляет собой матрицу светочувствительных элементов размера N х К. Для выполнения анализа матрица ФПЗС ориентируется относительно ткани так, как показано на рисунке 1.7.

Рисунок 1.7 - Ориентация матрицы ФПЗС относительно ткани
В общем случае процесс преобразования оптического сигнала е(х,у), осуществляемый матрицей ФПЗС, можно представить следующим образом:
Е(i,j)=kе(iТДХ,jТДУ), (1.8)
где: Е(i,j) - выходной сигнал матрицы, k - коэффициент пропорциональности.
Применительно к решаемой задаче анализа двумерное изображение удобней рассматривать как совокупность одномерных сигналов, измеренных вдоль строк изображения:
Еj(i)=kej(1ТДx), j=0÷N-1. (1.9)
Характерный вид сигнала Ej(i) одной из строк изображения представлен на рисунке 1.8.

Рисунок 1.8 – Фрагмент сигнала Ej(i)
Представленный сигнал соответствует реальному образцу ткани с полотняным переплетением. При этом матрица ФПЗС воспринимает отраженный от поверхности ткани световой поток.
Сигнал Ej(i) рассматривается как сумма полезной составляющей a(i) и составляющей A(i), обусловленной общей интенсивностью освещения. Считается, что составляющая a(i) обусловлена присутствием уточных нитей. Причем уточным нитям соответствуют положительные полуволны составляющей a(i) с амплитудами аk. Реальные сигналы Ej(i) характеризуются непостоянством величины составляющей A(i) и значительным разбросом амплитуд положительных полуволн аk, соответствующих различным нитям утка.
В соответствии с координатной методикой, определение положения уточных нитей осуществляется следующим образом: идентифицируются координаты расположения уточных нитей. Идентифицированные координаты уточных нитей связываются в множества, соответствующие одноименным нитям утка [4].
За координаты уточных нитей принимаются координаты точек локальных максимумов iok (смотреть рисунок 1.3) сигнала Ej(i), где j=0÷N-l.
С учетом дискретного характера задачи точка iok считается точкой локального максимума, если для нее выполнено условие:
Еj(i0k-1)≤Еj(iоk)>Еj(iоk+1). (1.10)
При дополнительном условии существования хотя бы одного i в интервале i0k-1 <i< i0k, для которого выполняется неравенство:
Еj(1)<Еj(i+1). (1.11)
Предложенный метод идентификации координат расположения нитей слабо чувствителен к непостоянству величины составляющей A(i) и разбросу амплитуд положительных полуволн ak. Метод обладает высокой достоверностью определения координат уточных нитей. В процессе исследований определено, что достоверность идентификации координат уточных нитей существенно зависит от коэффициента масштаба:
γ=ТДХ/ТН, (1.12)
где ТН - период повторения уточных нитей, ТДХ -период дискретизации равный расстоянию между светочувствительными элементами матрицы ФПЗС. Путем оптимального выбора коэффициента масштаба γ можно существенно повысить достоверность идентификации координат уточных нитей.
Связывание точек максимумов осуществляется на основании критерия принадлежности точек максимумов одноименным нитям: две точки максимумов i0, j и io, j+1, лежащие на осях xj и xj+1 и принадлежащие одной нити утка, не могут быть смещены в направлении осей xj более чем на расстояние δ:
|i0, j – i0, j+1 | ≤ δ. (1.13)
От величины интервала поиска δ зависит достоверность связывания точек максимумов. Рассмотрено влияние величины δ на достоверность связывания точек максимумов, определены критерии выбора величины δ. На основании условия (1.4) построен алгоритм позволяющий связывать точки максимумов в множества по признаку принадлежности одноименным нитям утка.
Схема работы алгоритма связывания точек максимумов изображена на риcунке 1.9.

Рисунок 1.9 – Схема работы алгоритма
Реальные сигналы, поступающие от ФПЗС преобразователя, оказываются искажены действием различного рода помех. Для повышения достоверности идентификации координат уточных нитей исходное изображение обрабатывается цифровым фильтром. С учетом времени обработки оптимальный эффект дает обработка сигналов Ej(i) полосовым рекурсивным фильтром второго порядка:
Еvj(i)=a0Еj(i)+а1Еj(i-1)+b1Еvj(i-1)+b2Еv(i-2), j=0÷N-l, (1.14)
где: Ej(i) - отсчетные значения входного сигнала фильтра; Еvj(i) - отсчетные значения выходного сигнала фильтра.
Применение данного фильтра на тканях со сложными переплетениями позволяет повысить количество идентифицированных нитей на 30-40 %.
1.11 Спектральный метод анализа изображения
Полезная составляющая a(i) сигнала Ej(i) представляет собой периодический процесс с законом, близким к гармоническому. Это позволяет представить ее в виде синусоидальных функций:
Yj(i)= Ajsin[2πfHi+φ(j)], i=0÷K-l, j=0÷N-l. (1.15)
Значения функции φ(j) в выражении 1.16 определяют начальную фазу составляющих Yj(i) на каждой из осей Xj. Смещение уточных нитей на осях Xj и Xj+1 определяет приращение ∆ φ функции φ(j). Для ткани с перекосом утка (рисунок 1.10) можно записать:
Не нашли, что искали? Воспользуйтесь поиском: